Multiplying Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn how to multiply fractions with easy-to-follow steps and visual examples!
What are Fractions?

A fraction represents parts of a whole. The top number (numerator) tells how many parts we have, and the bottom number (denominator) tells how many equal parts the whole is divided into.
For example, if you have 3 slices of a pizza that was cut into 8 equal slices, you have 3/8 of the pizza. Fractions are everywhere in our daily lives - when we share food, measure ingredients, or tell time!
Math Fact!
The word "fraction" comes from the Latin word "fractio" which means "to break". This makes sense because fractions break whole numbers into smaller parts!
How to Multiply Fractions
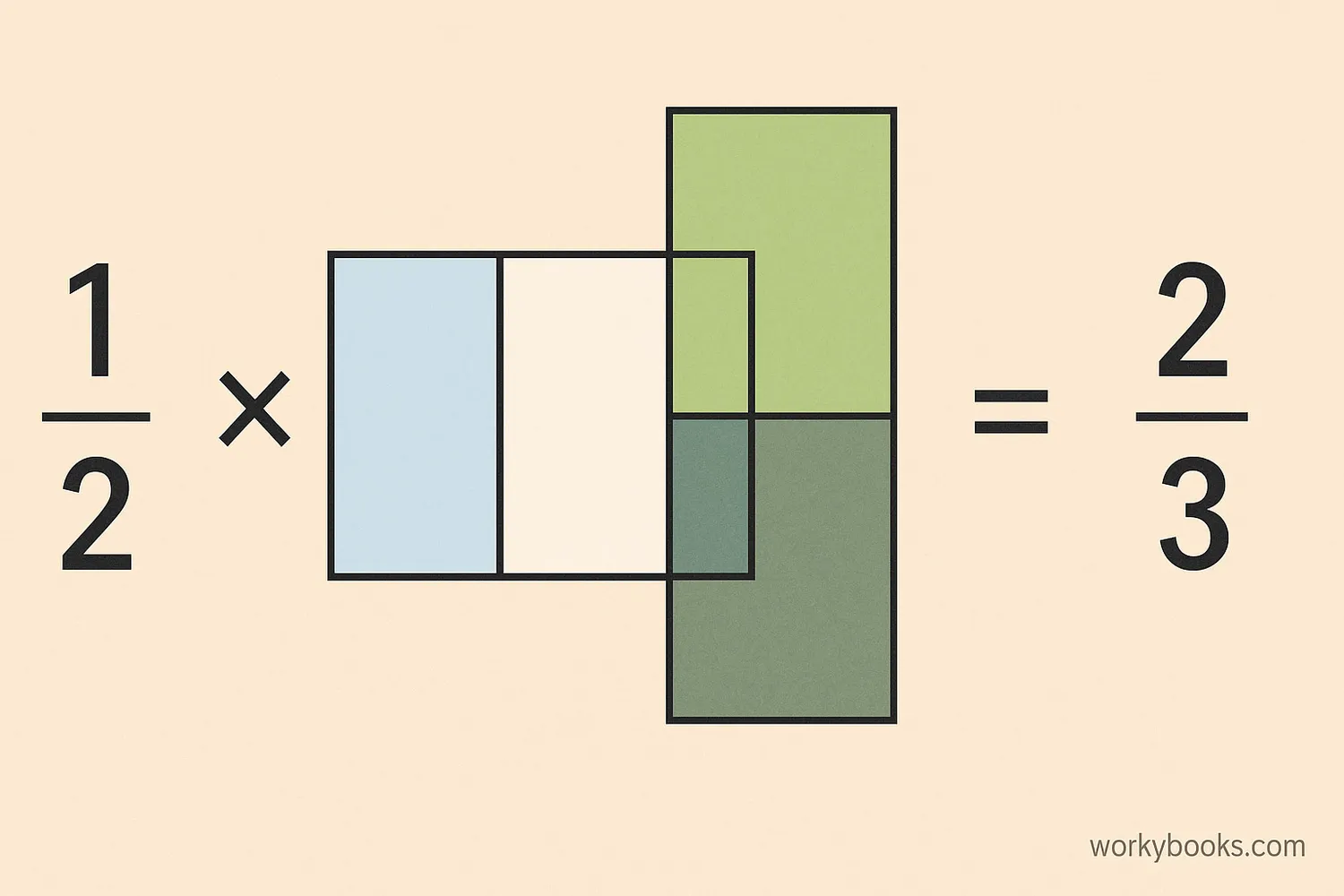
Multiplying fractions might seem tricky at first, but it's actually simpler than adding or subtracting them! Here's the basic rule:
Let's break it down into simple steps:
Multiply Numerators
Multiply the top numbers together
Multiply Denominators
Multiply the bottom numbers together
Simplify
Reduce the fraction to its simplest form
For example, to multiply 2/3 × 3/4:
Multiply numerators: 2 × 3 = 6
Multiply denominators: 3 × 4 = 12
So, 2/3 × 3/4 = 6/12
Then simplify: 6/12 = 1/2
Visual Examples
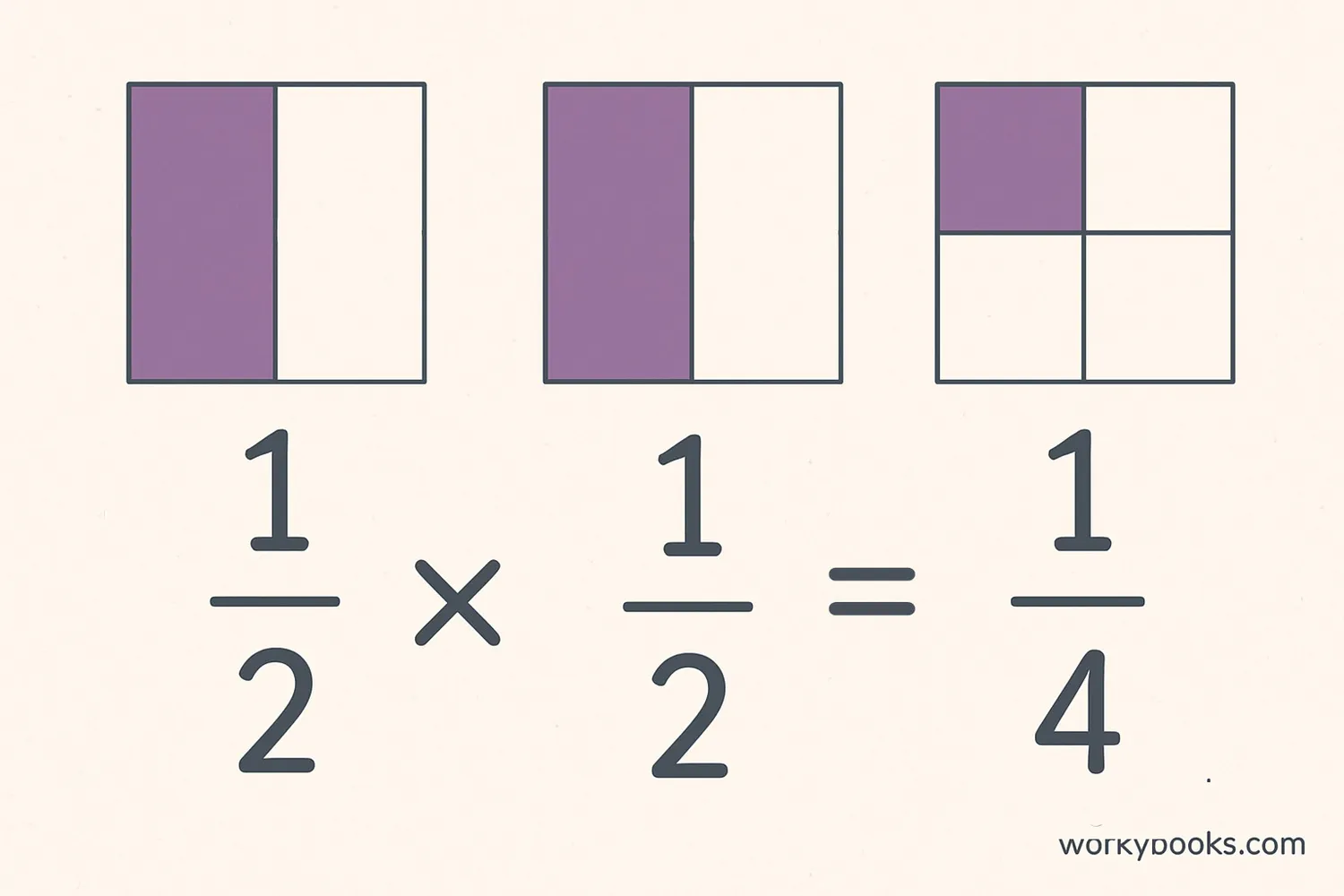
Let's look at a visual example. When we multiply 1/2 × 1/2:
Notice how multiplying 1/2 by 1/2 gives us 1/4. This makes sense because if you take half of a half, you get a quarter!
Try This!
If you have 2/3 of a chocolate bar and you eat 1/2 of that piece, what fraction of the whole chocolate bar did you eat? (Answer: 2/3 × 1/2 = 2/6 = 1/3)
Simplifying Your Results
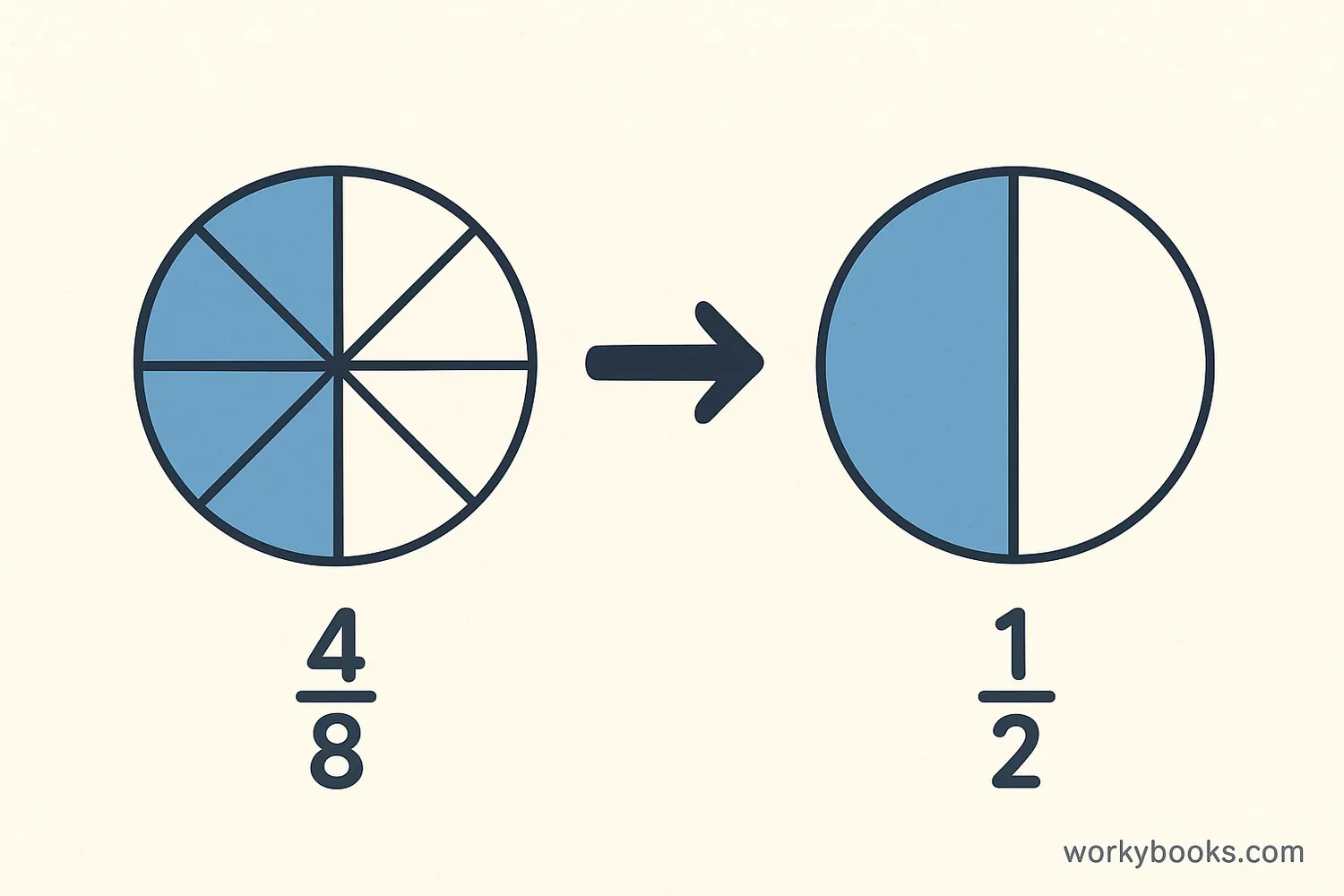
After multiplying fractions, we often need to simplify the result. Simplifying means writing the fraction in its simplest form by dividing both the numerator and denominator by their greatest common factor.
Find Common Factors
Look for numbers that divide evenly into both the numerator and denominator
Divide
Divide both numerator and denominator by the same number
Check
Make sure no more common factors remain
For example, if you get 6/12 as a result:
6 and 12 can both be divided by 6
6 ÷ 6 = 1 and 12 ÷ 6 = 2
So, 6/12 simplifies to 1/2
Math Tip!
You can simplify before multiplying to make calculations easier! If numerators and denominators have common factors, you can cancel them out before multiplying.
Multiplying Whole Numbers and Fractions
When multiplying a whole number by a fraction, remember that any whole number can be written as a fraction with a denominator of 1. For example, 3 = 3/1.
Let's break it down:
Convert to Fraction
Write the whole number as a fraction with denominator 1
Multiply
Multiply numerators and denominators as usual
Simplify
Write the answer as a proper fraction or mixed number
Another example: 4 × 3/8
4 × 3/8 = 4/1 × 3/8 = (4 × 3)/(1 × 8) = 12/8 = 3/2 = 1 1/2
Practice Quiz
Test your fraction multiplication skills with this quiz! Answer all 5 questions to see how much you've learned.
Frequently Asked Questions
Here are answers to some common questions about multiplying fractions:
Math Trivia
Discover some fascinating facts about fractions and mathematics!
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they mainly used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fraction Words
The word "numerator" comes from a Latin word meaning "counter," while "denominator" comes from a Latin word meaning "namer." This makes sense because the numerator counts the parts, and the denominator names how many parts make a whole.
Fractions in Music
Fractions are essential in music! Time signatures like 3/4 or 4/4 are actually fractions that tell musicians how many beats are in each measure and which note gets one beat.
Fractions in Cooking
When you double a recipe, you're using fraction multiplication! If a recipe calls for 3/4 cup of flour and you want to make twice as much, you calculate 2 × 3/4 = 6/4 = 1 1/2 cups.


