Multiplying Fractions by Whole Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn how to multiply fractions by whole numbers with step-by-step examples and practice!
What is Multiplying Fractions by Whole Numbers?
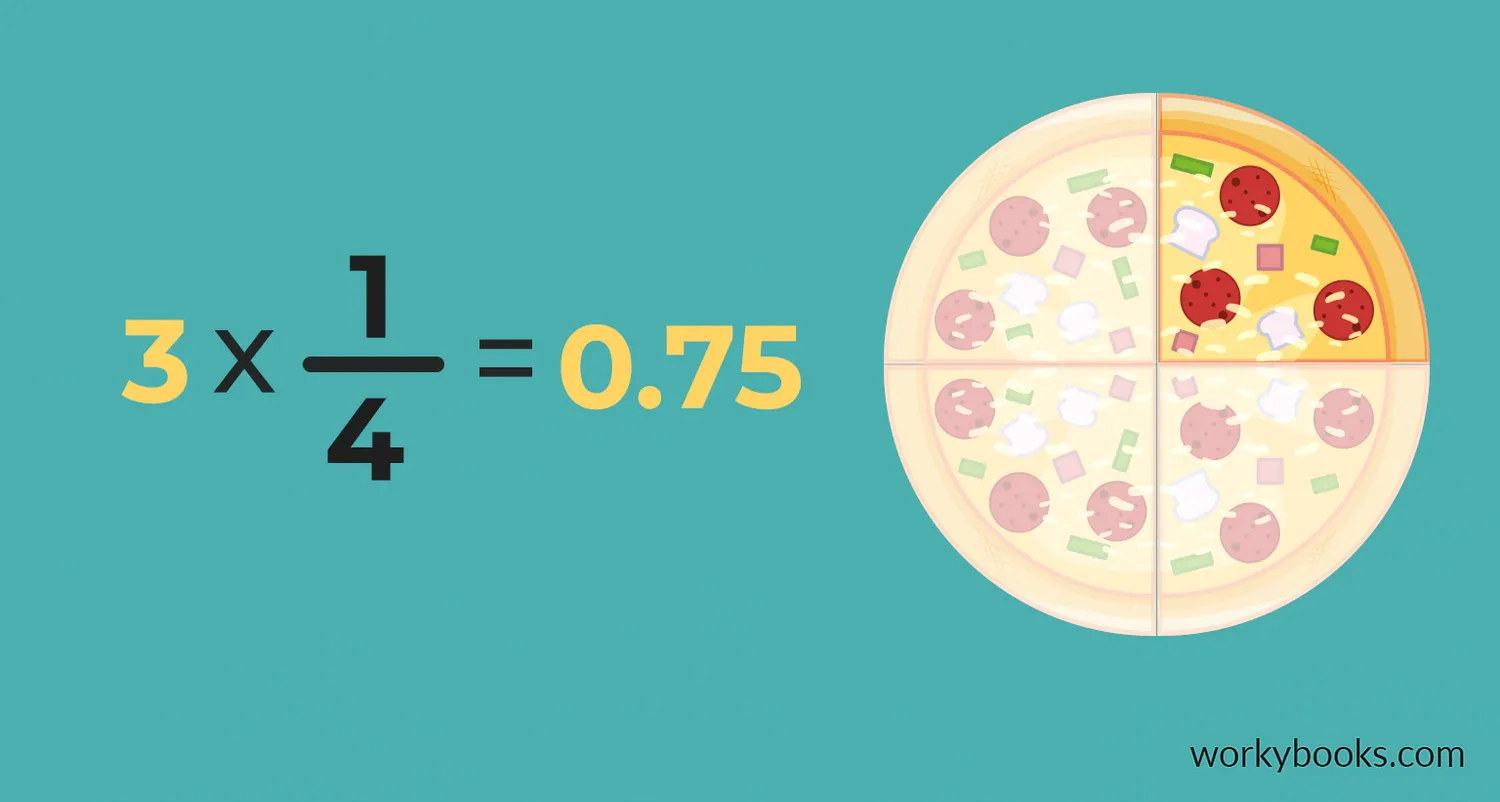
Multiplying a fraction by a whole number means finding a part of that whole number. It's like saying "I want 3 groups of 1/4" or "I want 2/3 of 5." This is an important math skill that helps us solve real-world problems.
When we multiply a fraction by a whole number, we're essentially adding the fraction to itself multiple times. For example, 3 × 14 is the same as 14 + 14 + 14.
Math Fact!
Any whole number can be written as a fraction by putting it over 1. For example, 5 becomes 51.
How to Multiply Fractions by Whole Numbers
Multiplying fractions by whole numbers is easier than you might think! Just follow these steps:
Write the Whole Number as a Fraction
Place the whole number over 1. For example, 3 becomes 31.
Multiply the Numerators
Multiply the top numbers (numerators) together.
Multiply the Denominators
Multiply the bottom numbers (denominators) together.
Simplify
Reduce the fraction to its simplest form if possible.
Remember: The denominator stays the same when you multiply a fraction by a whole number because we're finding parts of a whole, not changing the size of the parts.
Examples of Multiplying Fractions by Whole Numbers
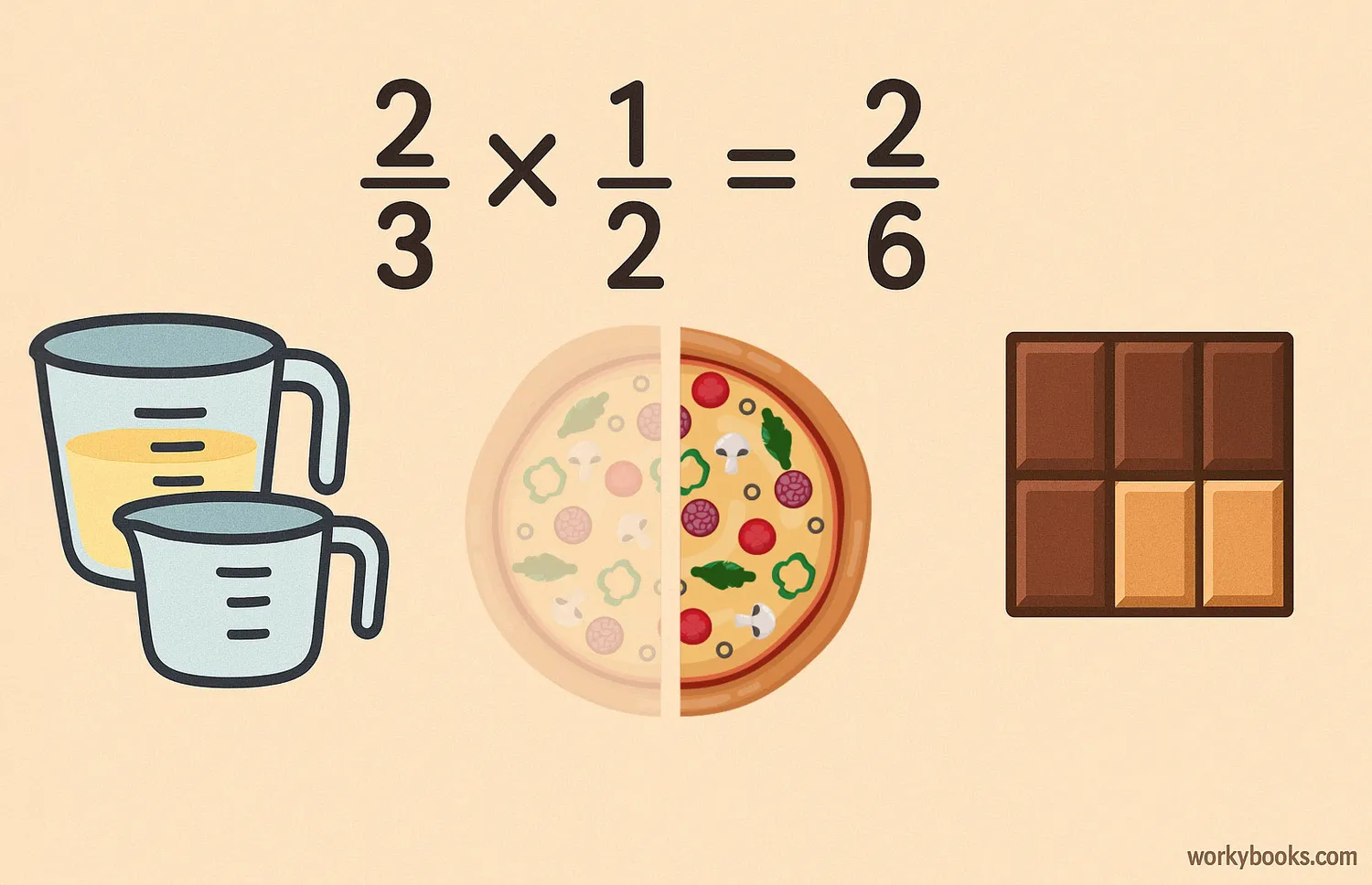
Let's look at some examples to see how fraction multiplication works:
Example 1: 3 × 14
Step 1: Write 3 as 31
Step 2: Multiply numerators: 3 × 1 = 3
Step 3: Multiply denominators: 1 × 4 = 4
Step 4: The answer is 34
Example 2: 5 × 23
Step 1: Write 5 as 51
Step 2: Multiply numerators: 5 × 2 = 10
Step 3: Multiply denominators: 1 × 3 = 3
Step 4: The answer is 103 or 3 13
Example 3: 2 × 35
Step 1: Write 2 as 21
Step 2: Multiply numerators: 2 × 3 = 6
Step 3: Multiply denominators: 1 × 5 = 5
Step 4: The answer is 65 or 1 15
Notice that when we multiply a fraction by a whole number, the product can be greater than 1. This happens when the numerator is larger than the denominator, creating what we call an improper fraction.
Visual Representation
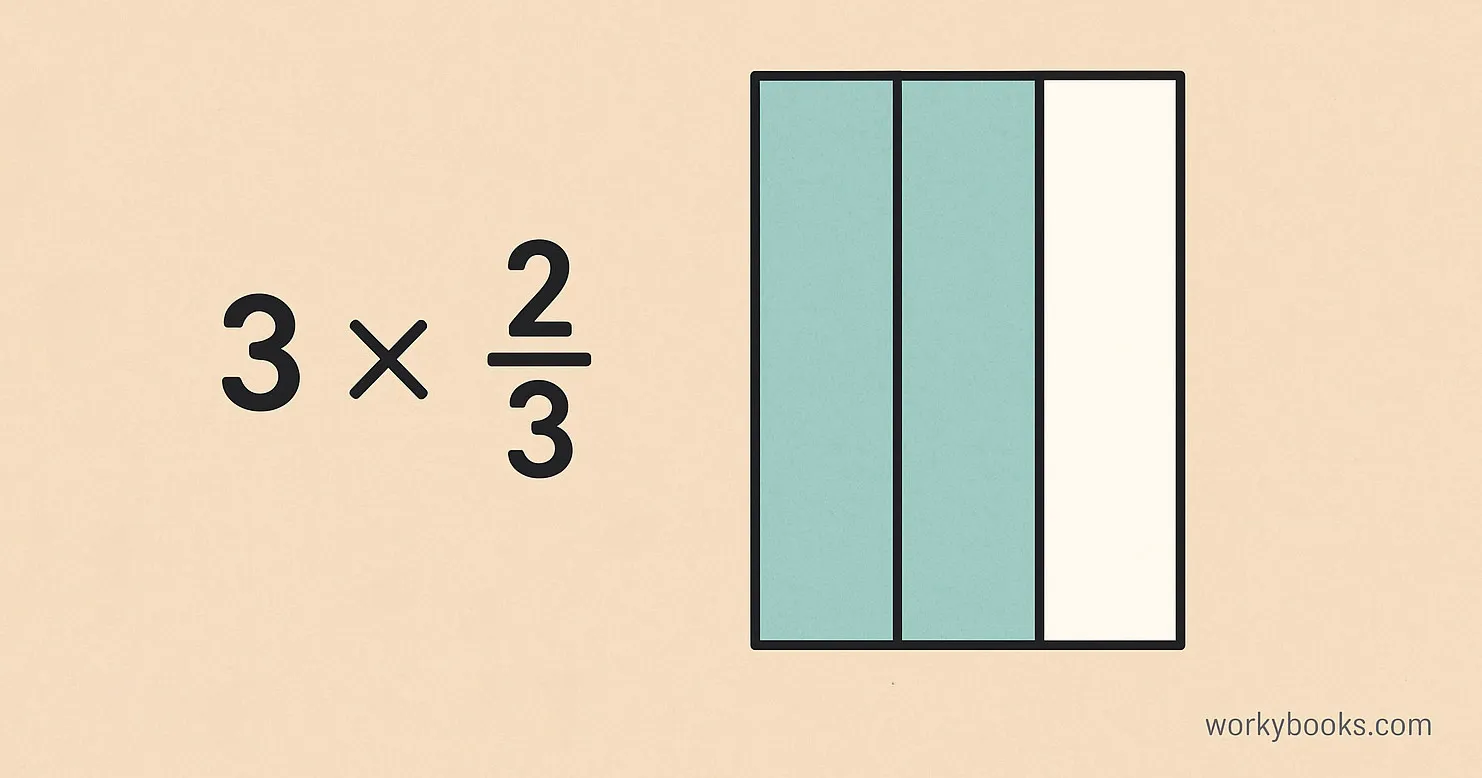
Using visual models can help us understand what happens when we multiply fractions by whole numbers. Let's look at 3 × 23:
First Whole
Imagine a whole divided into 3 equal parts with 2 parts shaded: 23
Second Whole
Another whole with 2 out of 3 parts shaded: 23
Third Whole
A third whole with 2 out of 3 parts shaded: 23
Total
We have 6 shaded parts out of 3 wholes, which is 2 whole units: 63 = 2
Visual models show us that 3 × 23 means we have 3 groups of 23, which equals 2 whole units.
Practice Quiz
Test your fraction multiplication knowledge with this quiz! Answer all 5 questions to see how much you've learned.
Frequently Asked Questions
Here are answers to some common questions about multiplying fractions by whole numbers:
Math Trivia
Discover some interesting facts about fractions and multiplication!
Ancient Fractions
The ancient Egyptians used fractions over 4,000 years ago, but they only used unit fractions (fractions with 1 as the numerator). They would write 3/4 as 1/2 + 1/4!
Fraction Origins
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent broken or parts of whole numbers.
Multiplying Magic
When you multiply a whole number by a fraction less than 1, the product is smaller than the original whole number. But when you multiply by a fraction greater than 1, the product is larger!
Fractions in Music
Musical notes are based on fractions! A whole note lasts 4 beats, a half note lasts 2 beats, a quarter note lasts 1 beat, and an eighth note lasts half a beat.





