Multiplying Fractions with Mixed Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn how to multiply fractions with mixed numbers through simple steps and visual examples!
What Are Mixed Numbers?
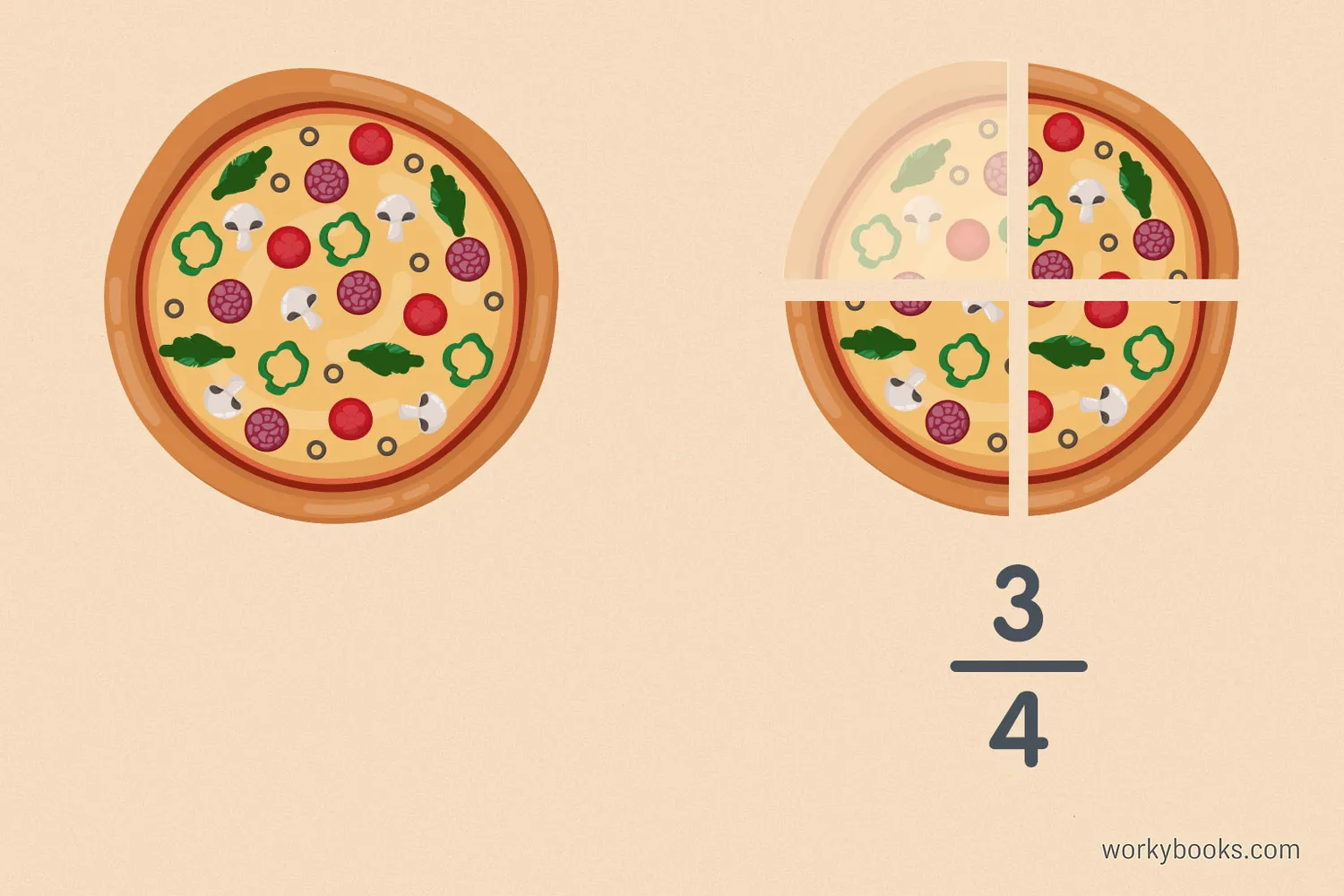
A mixed number is a combination of a whole number and a proper fraction. For example, 2 ½ represents 2 whole units plus half of another unit. Mixed numbers are useful for representing quantities that are more than a whole but not a whole number.
Think of a mixed number like having whole pizzas and part of another pizza. If you have 2 whole pizzas and half of a third pizza, you have 2 ½ pizzas.
Math Fact!
Mixed numbers are also called mixed fractions. The whole number part and the fraction part are added together to make the complete value.
Converting Mixed Numbers to Improper Fractions
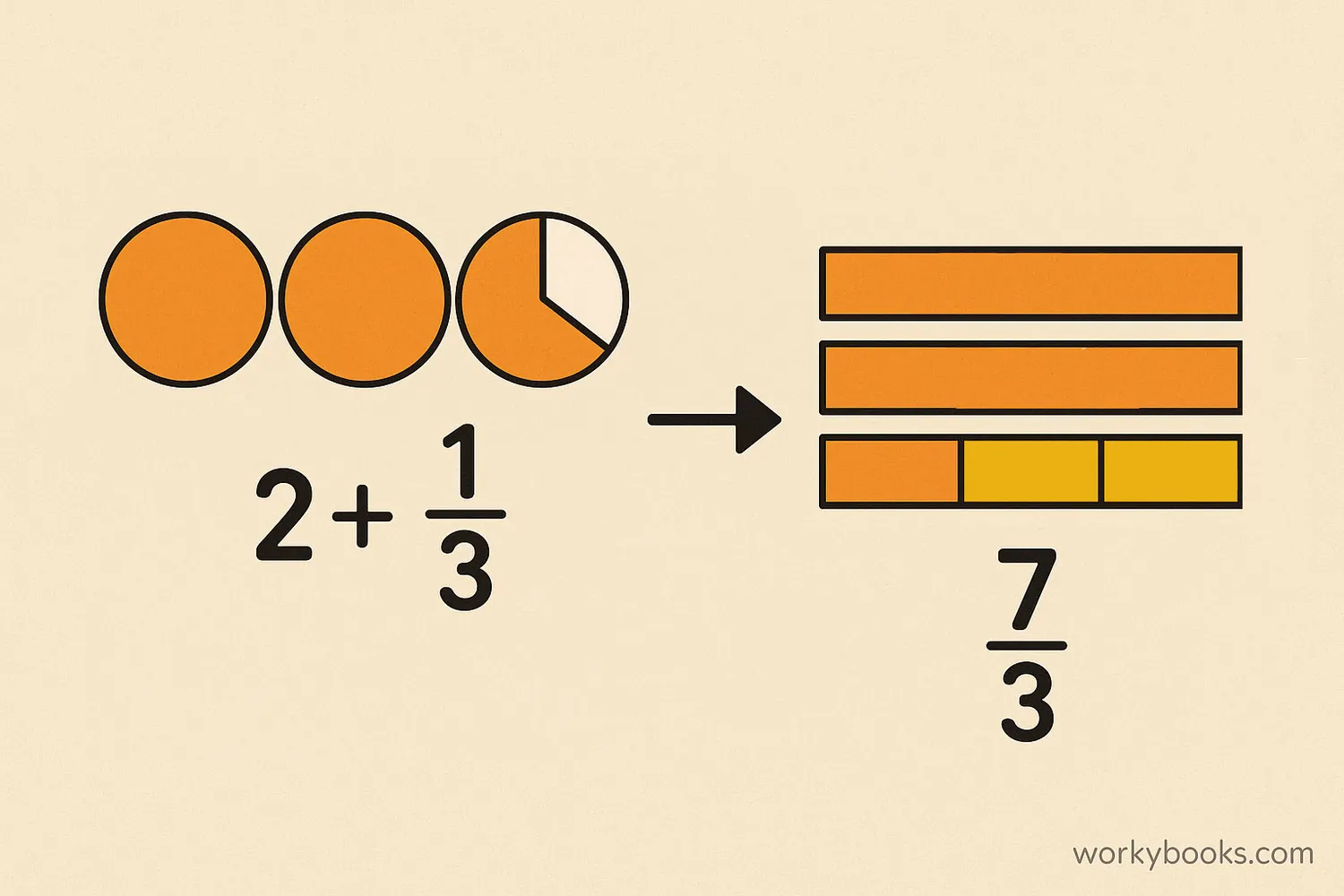
Before we can multiply mixed numbers with fractions, we need to convert the mixed numbers to improper fractions. An improper fraction has a numerator larger than its denominator.
Here's how to convert a mixed number to an improper fraction:
Multiply
Multiply the whole number by the denominator of the fraction
Add
Add the result to the numerator of the fraction
Write
Write the sum over the original denominator
Step 1: 2 × 3 = 6
Step 2: 6 + 1 = 7
Step 3: 7/3
So, 2 ⅓ = 7/3
Steps for Multiplying Fractions with Mixed Numbers
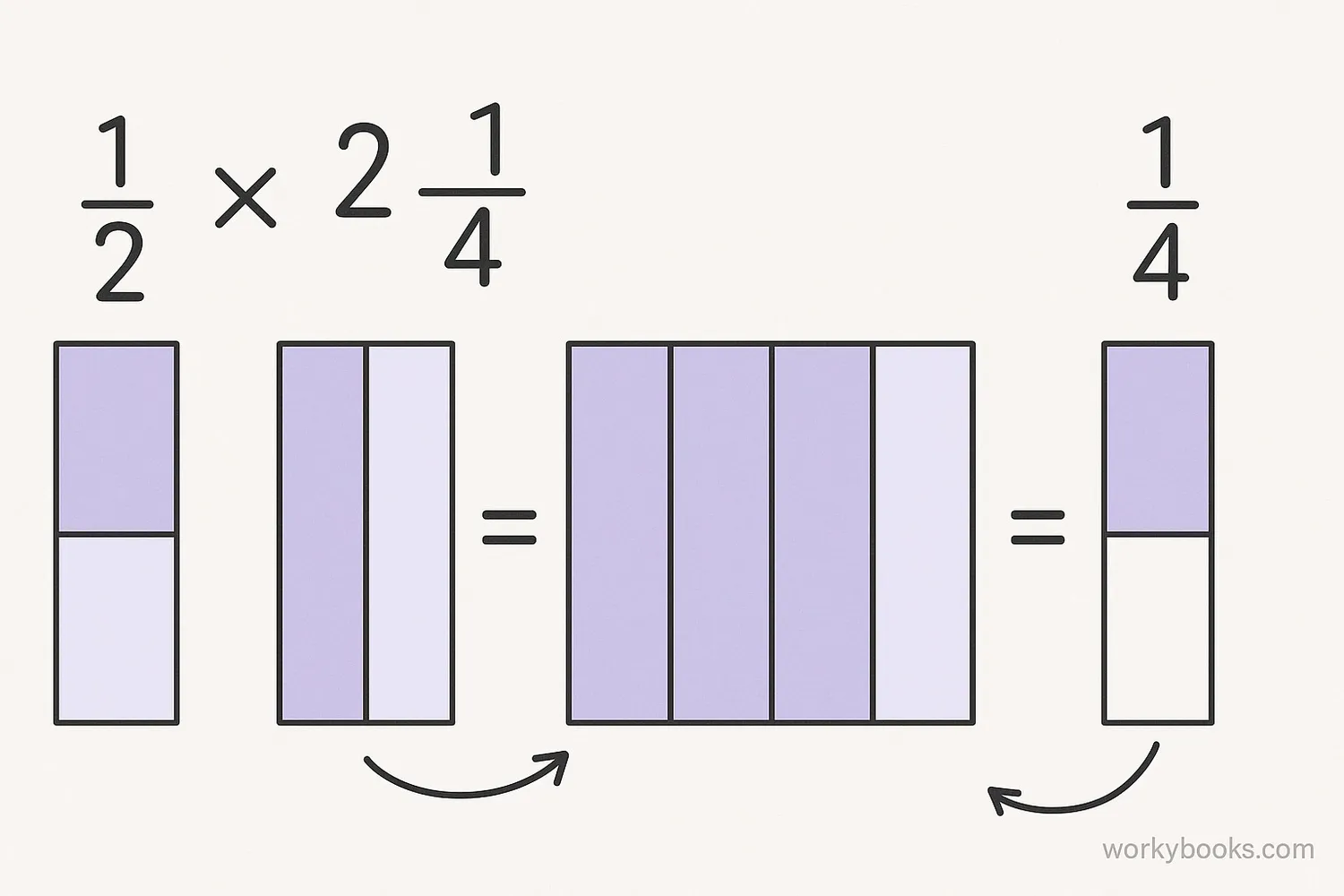
Now that you know how to convert mixed numbers, let's learn how to multiply them with fractions. Follow these steps:
Convert
Convert the mixed number to an improper fraction
Multiply
Multiply the numerators together
Multiply
Multiply the denominators together
Simplify
Simplify the result if possible
Step 1: Convert 2 ¼ to improper fraction: (2×4 + 1)/4 = 9/4
Step 2: Multiply numerators: 1 × 9 = 9
Step 3: Multiply denominators: 2 × 4 = 8
Step 4: The result is 9/8, which simplifies to 1 ⅛
Simplifying Your Results
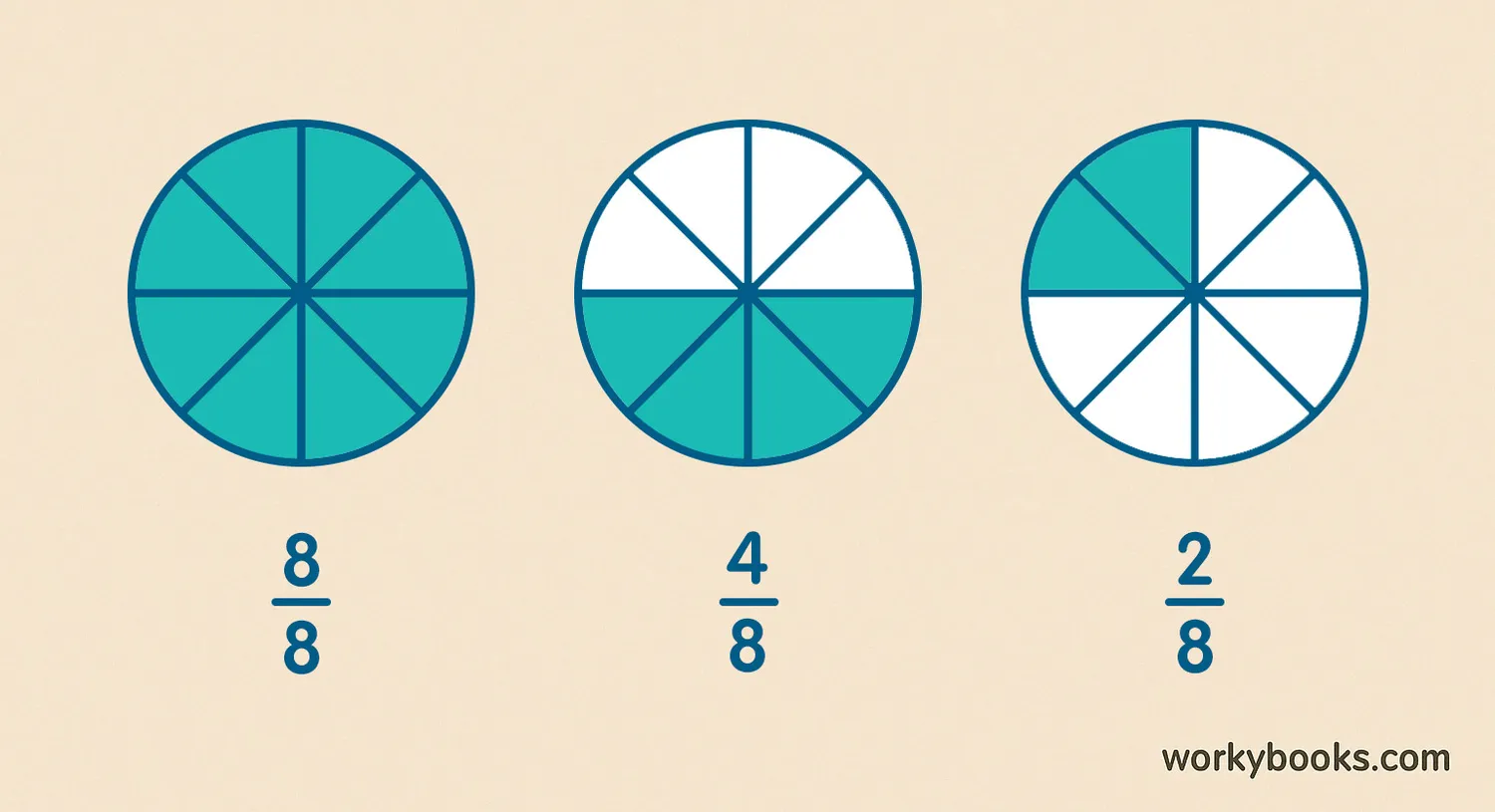
After multiplying, you often get a fraction that can be simplified. Simplifying means writing the fraction in its simplest form by dividing both the numerator and denominator by their greatest common factor (GCF).
Sometimes your result will be an improper fraction, which you might want to convert back to a mixed number.
The GCF of 12 and 8 is 4
12 ÷ 4 = 3
8 ÷ 4 = 2
So 12/8 simplifies to 3/2, which is 1 ½ as a mixed number
Math Tip!
Always check if your final answer can be simplified. This makes your answer cleaner and easier to understand.
Worked Examples
Let's work through some examples together. Follow each step carefully:
Step 1: Convert 1 ½ to improper fraction: (1×2 + 1)/2 = 3/2
Step 2: Multiply fractions: ⅔ × 3/2
Step 3: Multiply numerators: 2 × 3 = 6
Step 4: Multiply denominators: 3 × 2 = 6
Step 5: Result is 6/6 which simplifies to 1
Answer: 1
Step 1: Convert 2 ⅔ to improper fraction: (2×3 + 2)/3 = 8/3
Step 2: Multiply fractions: ¼ × 8/3
Step 3: Multiply numerators: 1 × 8 = 8
Step 4: Multiply denominators: 4 × 3 = 12
Step 5: Result is 8/12 which simplifies to ⅔ (dividing by 4)
Answer: ⅔
Step 1: Convert 1 ¼ to improper fraction: (1×4 + 1)/4 = 5/4
Step 2: Multiply fractions: ⅗ × 5/4
Step 3: Multiply numerators: 3 × 5 = 15
Step 4: Multiply denominators: 5 × 4 = 20
Step 5: Result is 15/20 which simplifies to ¾ (dividing by 5)
Answer: ¾
Practice Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned.
Frequently Asked Questions
Here are answers to some common questions about multiplying fractions with mixed numbers:
Math Trivia
Discover some interesting facts about fractions and mathematics!
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they mainly used unit fractions (fractions with 1 as the numerator). They would write other fractions as sums of unit fractions.
Fraction Origins
The word "fraction" comes from the Latin word "fractus" which means "broken." This makes sense because fractions represent parts of a whole thing that has been broken into pieces.
Never-Ending Fractions
Some fractions create decimals that go on forever! For example, 1/3 = 0.33333... with the 3 repeating infinitely. These are called repeating decimals.
Multiplication Magic
When you multiply two proper fractions (where numerator is smaller than denominator), the product is always smaller than both original fractions. For example, ½ × ½ = ¼, which is smaller than ½.





