Multiplying Mixed Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn how to multiply mixed numbers with easy explanations, step-by-step examples, and practice activities
What Are Mixed Numbers?
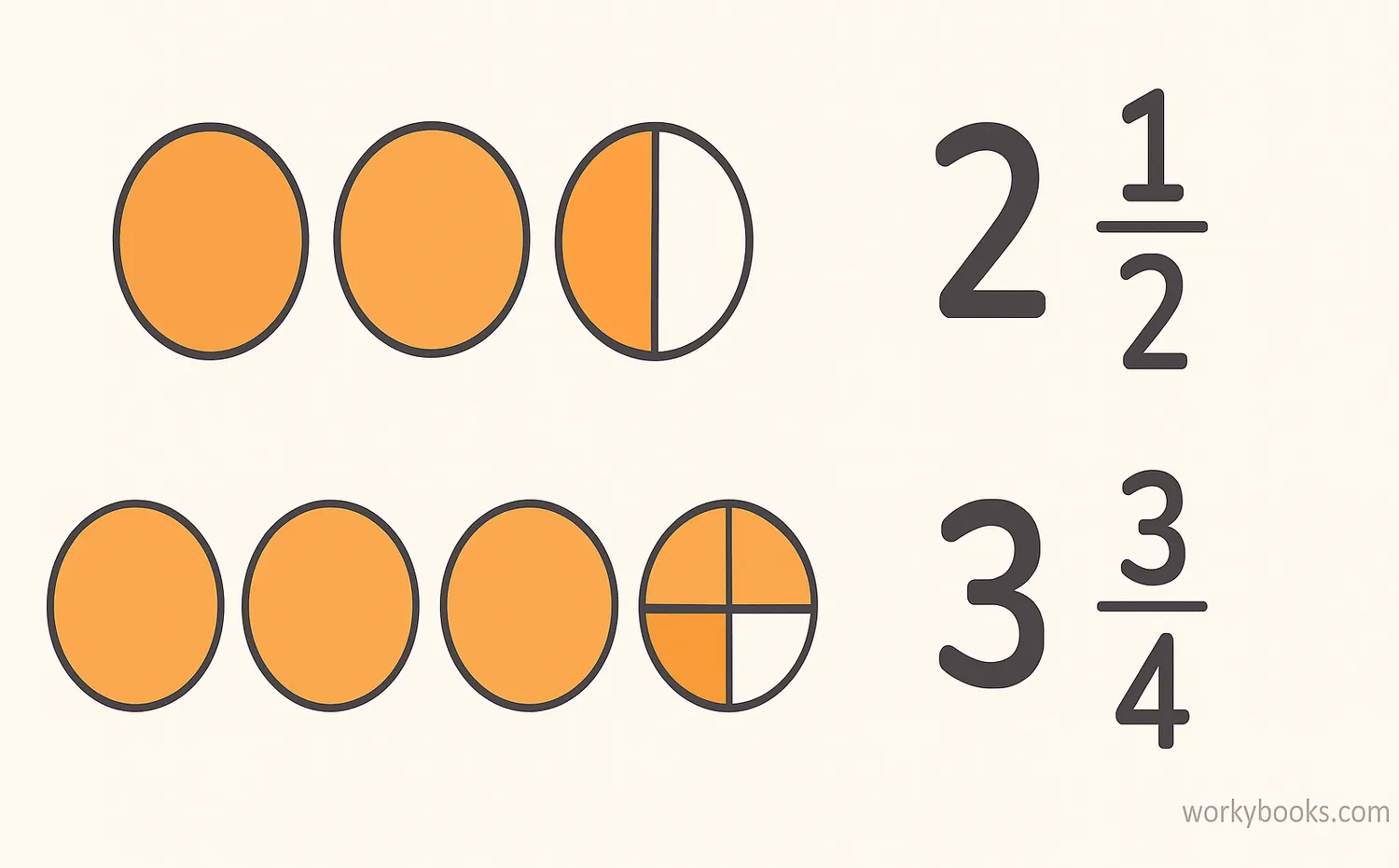
A mixed number is a combination of a whole number and a proper fraction. For example, 2½ (two and a half) is a mixed number where 2 is the whole number and ½ is the fractional part.
Mixed numbers are useful in everyday life. When you say "I drank 1½ glasses of water" or "We need 2¾ cups of flour for this recipe," you're using mixed numbers!
To multiply mixed numbers, we first need to convert them into improper fractions. An improper fraction has a numerator that is larger than its denominator, like 5/4 or 7/3.
Key Concept
Mixed numbers = Whole number + Fraction. To multiply them, convert to improper fractions first!
Steps to Multiply Mixed Numbers

Multiplying mixed numbers might seem tricky at first, but if you follow these steps, you'll become an expert!
Convert to Improper Fractions
Multiply the whole number by the denominator, then add the numerator. Keep the same denominator.
Example: 2½ becomes (2×2 + 1)/2 = 5/2
Multiply the Numerators
Multiply the numerators of both fractions together.
Example: 5/2 × 4/3 → Multiply 5 × 4 = 20
Multiply the Denominators
Multiply the denominators of both fractions together.
Example: 5/2 × 4/3 → Multiply 2 × 3 = 6
Simplify the Result
If possible, simplify the fraction by dividing numerator and denominator by their greatest common factor.
Example: 20/6 simplifies to 10/3
Convert Back to Mixed Number (if needed)
Divide the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the new numerator.
Example: 10/3 = 3⅓ (since 10÷3 = 3 with remainder 1)
Multiplication Formula
Examples of Multiplying Mixed Numbers

Let's work through some examples to see how we multiply mixed numbers in action:
Example 1: 2½ × 1⅓
Step 1: Convert to improper fractions
2½ = 5/2 1⅓ = 4/3
Step 2: Multiply numerators and denominators
5/2 × 4/3 = (5×4)/(2×3) = 20/6
Step 3: Simplify
20/6 = 10/3
Step 4: Convert to mixed number
10/3 = 3⅓
Answer: 2½ × 1⅓ = 3⅓
Example 2: 1¾ × 2½
Step 1: Convert to improper fractions
1¾ = 7/4 2½ = 5/2
Step 2: Multiply numerators and denominators
7/4 × 5/2 = (7×5)/(4×2) = 35/8
Step 3: Convert to mixed number
35/8 = 4⅜ (since 35÷8 = 4 with remainder 3)
Answer: 1¾ × 2½ = 4⅜
Example 3: 3⅔ × 2¼
Step 1: Convert to improper fractions
3⅔ = 11/3 2¼ = 9/4
Step 2: Multiply numerators and denominators
11/3 × 9/4 = (11×9)/(3×4) = 99/12
Step 3: Simplify
99/12 = 33/4 (dividing numerator and denominator by 3)
Step 4: Convert to mixed number
33/4 = 8¼ (since 33÷4 = 8 with remainder 1)
Answer: 3⅔ × 2¼ = 8¼
Remember
Always simplify your answer to its simplest form. This makes it easier to understand and work with.
Multiplying Mixed Numbers Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about multiplying mixed numbers:
Math Trivia
Discover interesting facts about fractions and mixed numbers:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they primarily used unit fractions (fractions with 1 as the numerator). They would express 3/4 as 1/2 + 1/4 rather than as a single fraction.
Fraction Words
The word "fraction" comes from the Latin "fractus" which means "broken". This makes sense because fractions represent parts of a whole—like a broken piece of something!
Never-Ending Fractions
Some fractions create never-ending, repeating decimals. For example, 1/3 = 0.33333... and 2/7 = 0.285714285714... These are called repeating decimals.
Practical Applications
Multiplying mixed numbers is especially useful in cooking (adjusting recipes), construction (calculating materials), and sewing (measuring fabric). These real-world applications make the skill valuable beyond the classroom.


