Multiplying Polynomials - Definition, Examples, Quiz, FAQ, Trivia
Learn how to multiply polynomials with step-by-step instructions, examples, and practice activities
What is Polynomial Multiplication?

Polynomial multiplication is the process of multiplying two or more polynomials together. A polynomial is an expression with variables, coefficients, and exponents that are combined using addition, subtraction, and multiplication.
Key parts of a polynomial:
- Term: A single part of a polynomial (like 3x² or -5)
- Coefficient: The number in front of a variable (like 3 in 3x²)
- Variable: A letter that represents a number (like x or y)
- Exponent: Shows how many times to multiply the variable (like 2 in x²)
When we multiply polynomials, we use the distributive property to make sure every term in the first polynomial multiplies every term in the second polynomial.
Key Concept
Multiplying polynomials is like giving out invitations to a party - you need to make sure everyone gets one!
Methods for Multiplying Polynomials
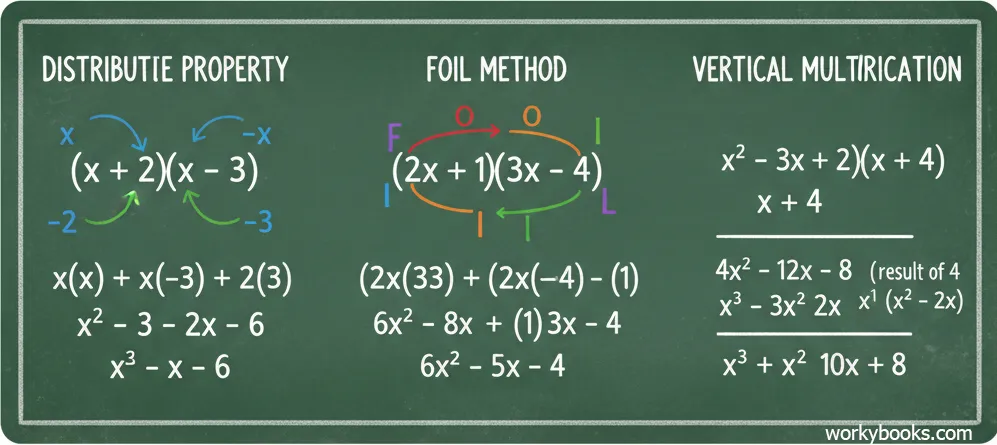
There are several methods for multiplying polynomials. The best method to use depends on the polynomials you're working with:
1. Distributive Property (Horizontal Method):
Multiply each term in the first polynomial by each term in the second polynomial, then combine like terms.
2. FOIL Method (for Binomials):
FOIL stands for First, Outer, Inner, Last. It's a special way to multiply two binomials.
3. Vertical Method:
Stack the polynomials like traditional multiplication, multiply each term, then add the results.
4. Box Method:
Create a box, place terms along edges, multiply to fill the boxes, then combine like terms.
Using the Distributive Property
Multiply each term in the first polynomial by each term in the second polynomial.
Simplify each multiplication by multiplying coefficients and adding exponents of like variables.
Combine like terms (terms with the same variable and exponent).
Multiplying Binomials
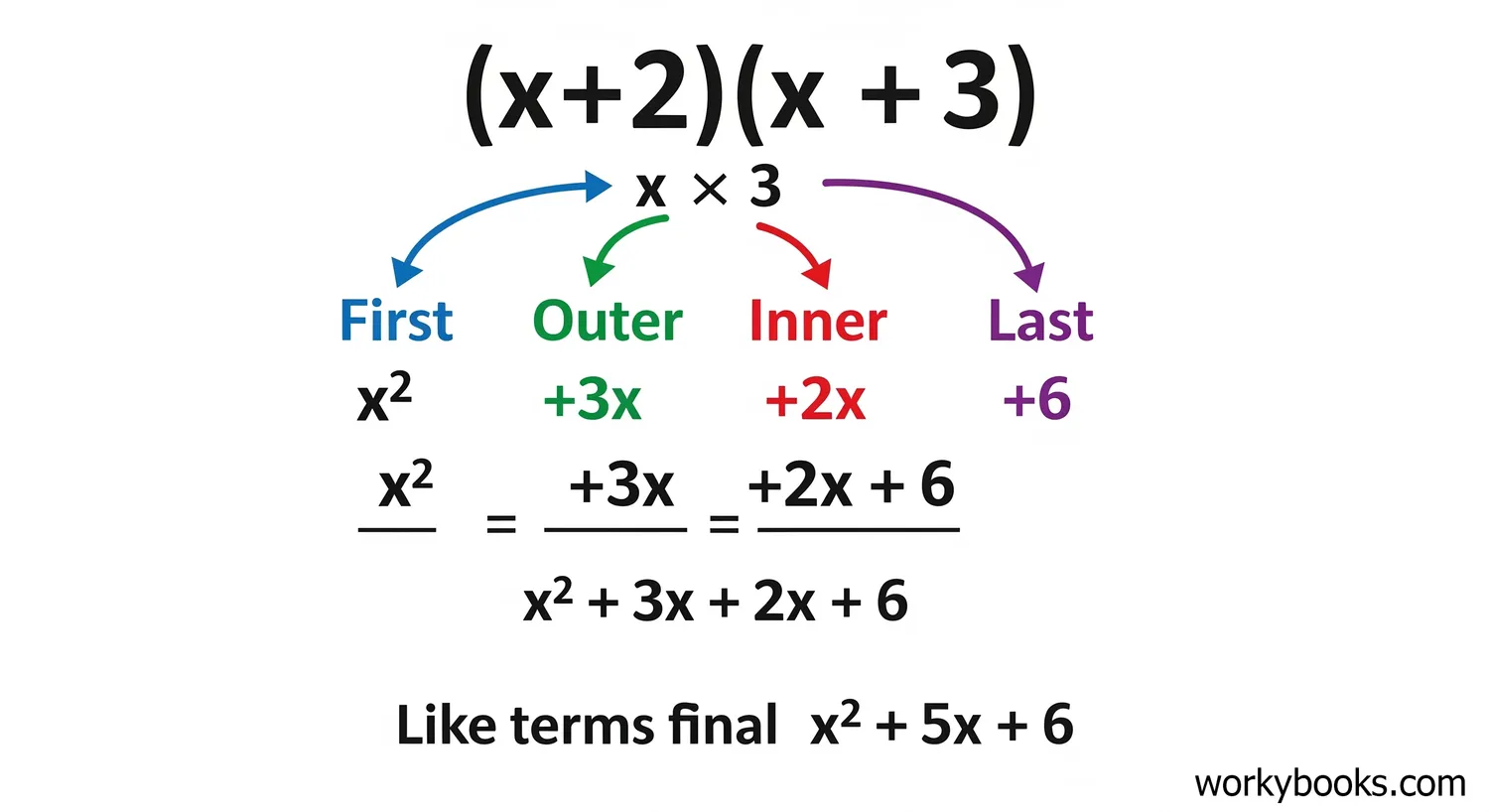
Binomials are polynomials with exactly two terms. When multiplying two binomials, we often use the FOIL method:
FOIL Method
First: a × c
Outer: a × d
Inner: b × c
Last: b × d
Multiplying Trinomials

Trinomials are polynomials with exactly three terms. Multiplying trinomials follows the same distributive property as other polynomials, but with more terms to keep track of.
When multiplying trinomials, it's helpful to use the vertical method or create a systematic approach to ensure you multiply every term in the first trinomial by every term in the second trinomial.
Remember
When multiplying polynomials, always double-check that you've multiplied every term by every other term. It's easy to miss one!
Polynomial Multiplication Examples
Let's look at some detailed examples of multiplying different types of polynomials:
Example 1: Monomial × Binomial
Polynomial Multiplication Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about multiplying polynomials:
Math Trivia
Discover interesting facts about polynomials and algebra:
Ancient Algebra
The word "algebra" comes from the Arabic word "al-jabr" which means "reunion of broken parts." This term was used in the title of a book written by the Persian mathematician Muhammad ibn Musa al-Khwarizmi around 820 CE.
Polynomial Degrees
The degree of a polynomial is the highest exponent of its variable. Polynomials are used in many real-world applications: linear (degree 1) for constant rates of change, quadratic (degree 2) for acceleration, and cubic (degree 3) for modeling volumes.
Polynomials in Space
NASA uses polynomial equations to calculate rocket trajectories and orbital paths. The complex calculations needed for space travel rely on multiplying and manipulating polynomials to model motion and predict paths accurately.
Computer Algebra Systems
Modern computer algebra systems can multiply polynomials with thousands of terms! These systems use sophisticated algorithms that are much more efficient than the methods we learn in school, but they're based on the same fundamental principles of distribution and combining like terms.





