Number System - Definition, Examples, Quiz, FAQ, Trivia
Understanding How We Count and Represent Numbers
What is a Number System?
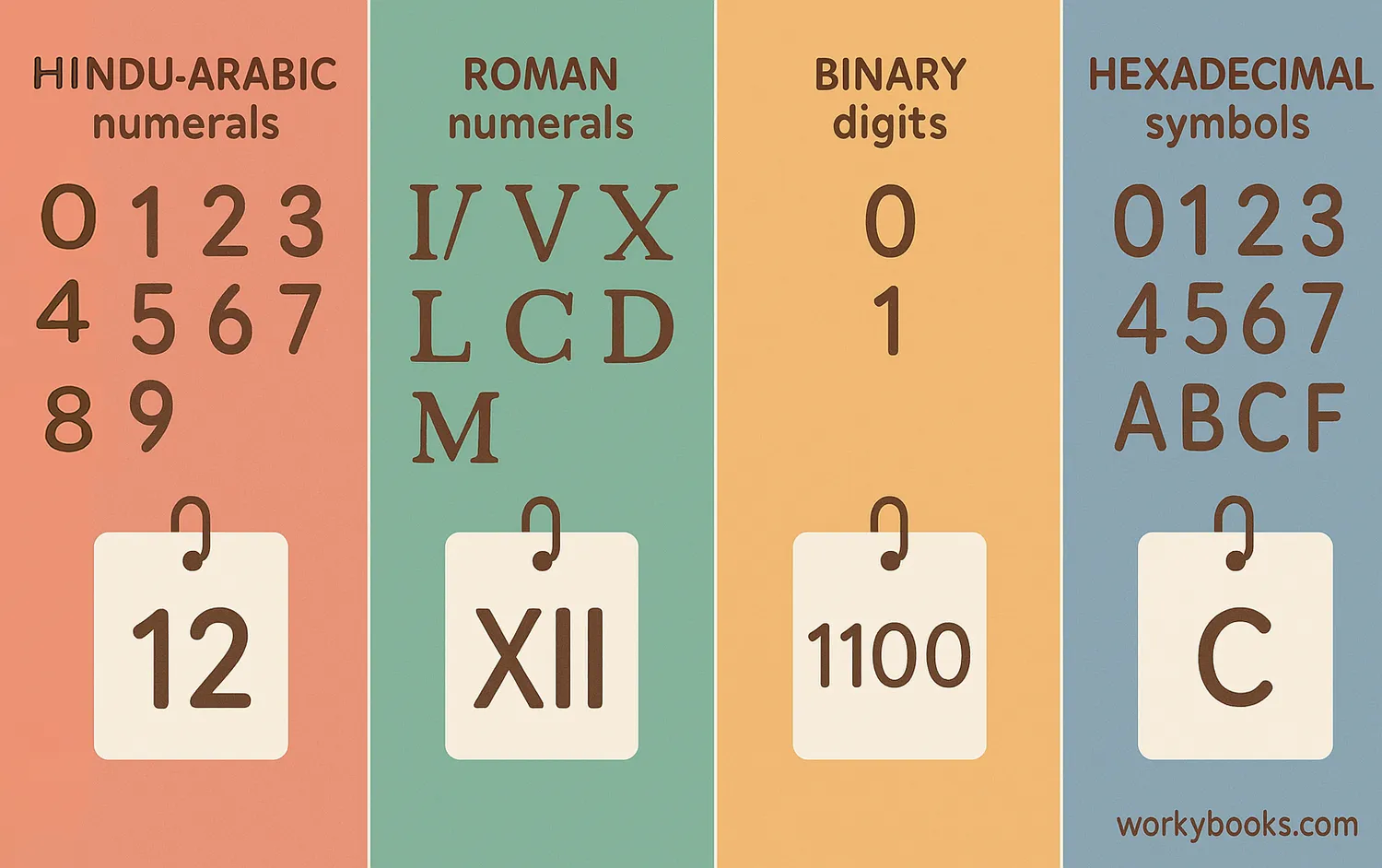
A number system is a way to represent numbers using symbols or digits. Think of it as a special language for counting and calculating!
Different number systems use different bases. The base tells us how many digits are available in that system. Our everyday number system is base 10 (decimal), which means it uses 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Math Fact!
The Hindu-Arabic numeral system we use today was developed in India around the 6th century and spread to Europe through Arab mathematicians. Before this, people used Roman numerals and other systems.
Decimal Number System

The decimal system is the number system we use every day. It's called base-10 because it uses 10 digits (0-9) and each place value represents a power of 10.
In the decimal system, the value of a digit depends on its position. For example, in the number 365:
Ones Place
The digit 5 means 5 ones (5 × 10⁰)
Tens Place
The digit 6 means 6 tens (6 × 10¹)
Hundreds Place
The digit 3 means 3 hundreds (3 × 10²)
So, 365 = (3 × 100) + (6 × 10) + (5 × 1). This place value system makes it easy to work with large numbers and perform calculations.
Binary Number System

The binary system is a base-2 number system that uses only two digits: 0 and 1. Computers use this system because electronic circuits can easily represent these two states (on/off, true/false).
In binary, each place value represents a power of 2. Let's look at how the binary number 1011 converts to decimal:
Rightmost Digit
1 × 2⁰ = 1 × 1 = 1
Next Digit
1 × 2¹ = 1 × 2 = 2
Next Digit
0 × 2² = 0 × 4 = 0
Leftmost Digit
1 × 2³ = 1 × 8 = 8
Adding these values together: 8 + 0 + 2 + 1 = 11. So, the binary number 1011 equals 11 in decimal.
Did You Know?
Every piece of information in a computer—numbers, text, images, and sounds—is ultimately stored and processed as binary numbers (0s and 1s).
Octal Number System
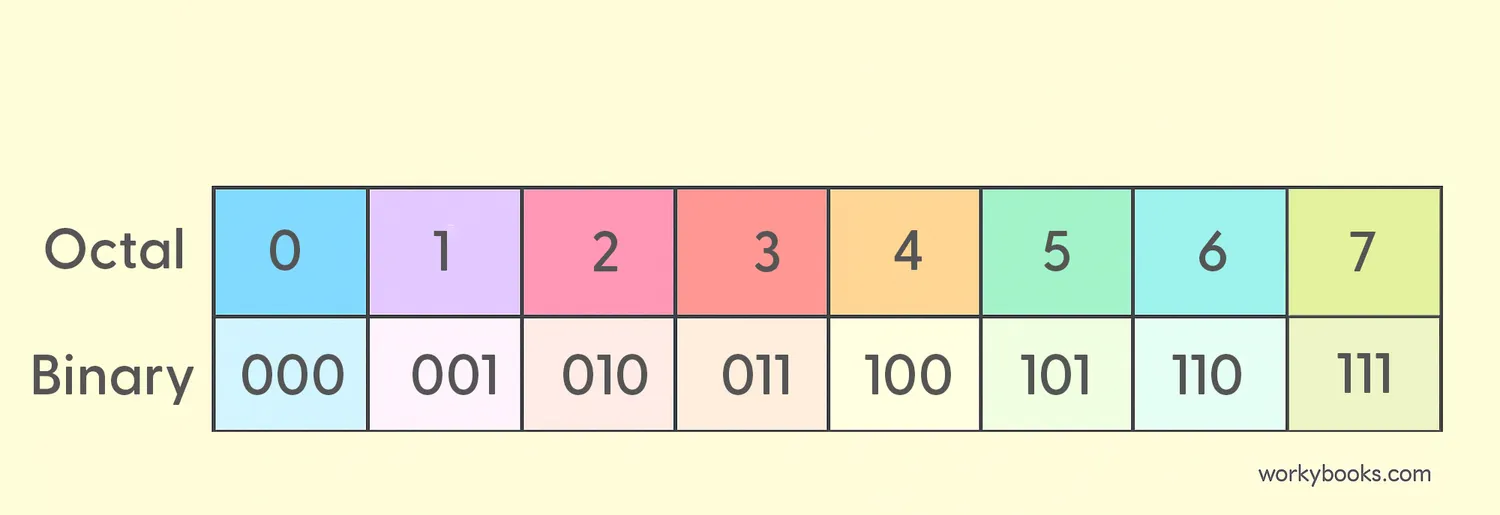
The octal system is a base-8 number system that uses digits from 0 to 7. It was commonly used in early computing because it's easy to convert between octal and binary.
Each place value in octal represents a power of 8. For example, the octal number 247 converts to decimal as:
Ones Place
7 × 8⁰ = 7 × 1 = 7
Eights Place
4 × 8¹ = 4 × 8 = 32
Sixty-fours Place
2 × 8² = 2 × 64 = 128
Adding these values: 128 + 32 + 7 = 167. So, the octal number 247 equals 167 in decimal.
Conversion Tip
Each octal digit corresponds to exactly three binary digits. For example, octal 5 is binary 101, and octal 7 is binary 111. This makes converting between these systems straightforward.
Hexadecimal Number System
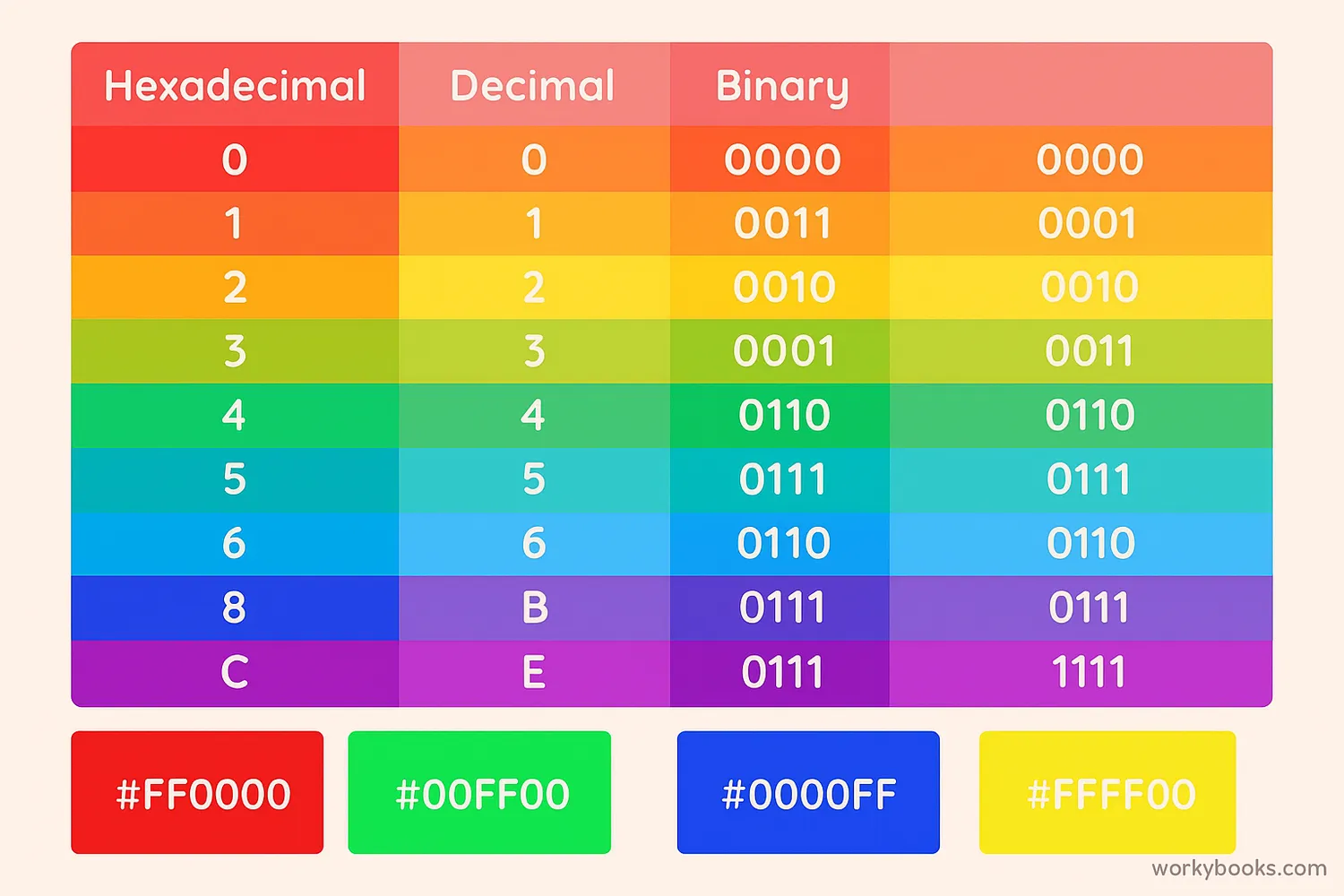
The hexadecimal system is a base-16 number system that uses 16 symbols: digits 0-9 and letters A-F (where A=10, B=11, C=12, D=13, E=14, F=15). It's widely used in computer programming and digital design.
Each place value in hexadecimal represents a power of 16. For example, the hexadecimal number 2A3 converts to decimal as:
Ones Place
3 × 16⁰ = 3 × 1 = 3
Sixteens Place
A × 16¹ = 10 × 16 = 160
256s Place
2 × 16² = 2 × 256 = 512
Adding these values: 512 + 160 + 3 = 675. So, the hexadecimal number 2A3 equals 675 in decimal.
Real-World Use
Hexadecimal is commonly used to represent colors in web design. For example, #FF0000 represents red, where FF is the maximum red value, and 00 represents no green or blue.
Number System Conversion
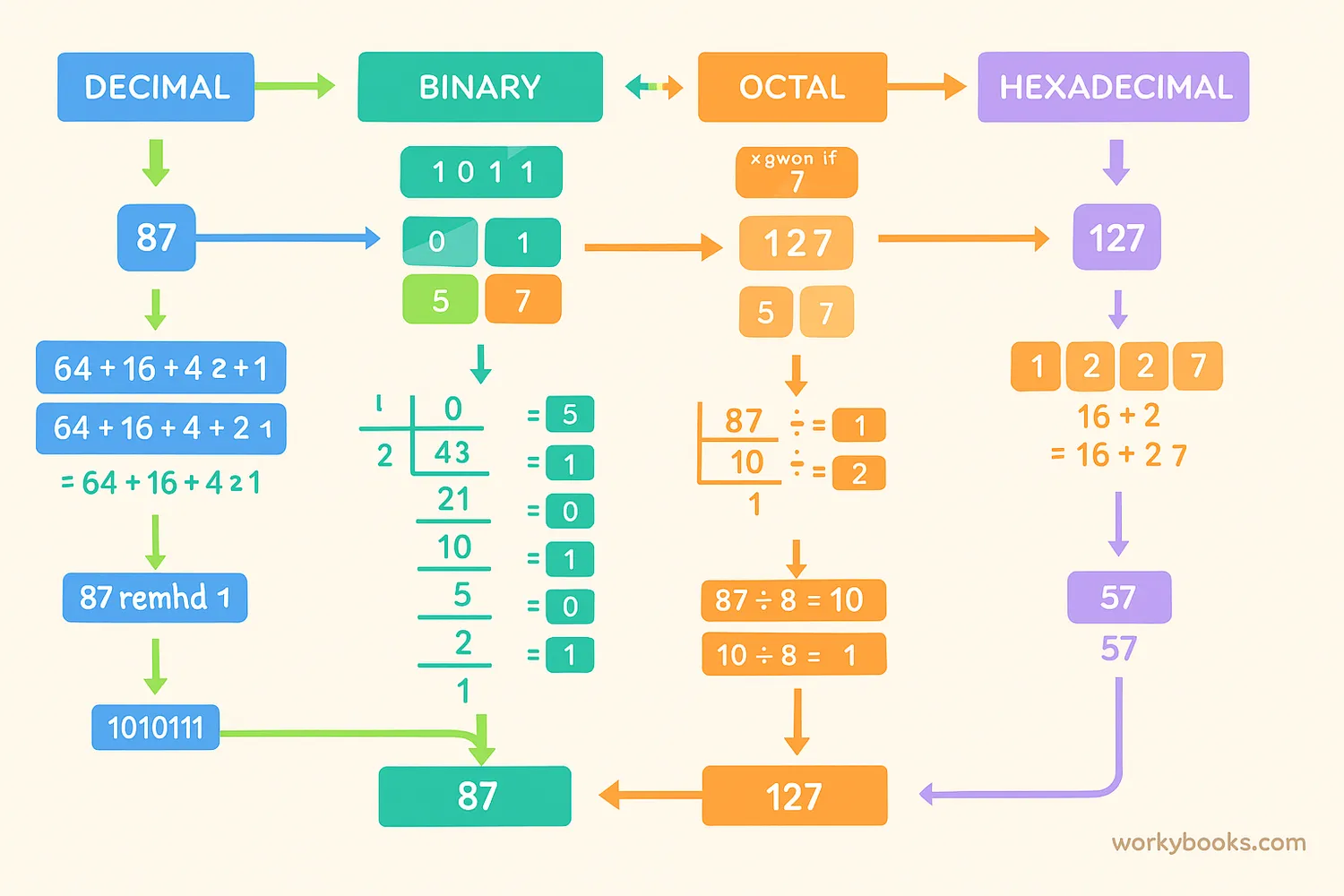
Converting between number systems might seem tricky, but it becomes easier with practice! Here are some basic conversion methods:
Decimal to Binary
Repeatedly divide by 2 and note remainders
Binary to Decimal
Multiply each digit by 2 raised to its position power
Binary to Hexadecimal
Group binary digits into sets of 4 and convert each group
Hexadecimal to Decimal
Multiply each digit by 16 raised to its position power
Let's try converting decimal 25 to binary:
25 ÷ 2 = 12 remainder 1
12 ÷ 2 = 6 remainder 0
6 ÷ 2 = 3 remainder 0
3 ÷ 2 = 1 remainder 1
1 ÷ 2 = 0 remainder 1
Reading the remainders from bottom to top: 11001. So, 25 in decimal is 11001 in binary.
Practice Makes Perfect
The more you practice converting between number systems, the easier it becomes. Start with small numbers and work your way up to larger ones!
Number System Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about number systems.
Frequently Asked Questions
Here are answers to some common questions about number systems:
Math Facts About Number Systems
Discover some fascinating facts about number systems and mathematics!
The Concept of Zero
The concept of zero as a number was developed in India around the 5th century. Before this, most number systems didn't have a symbol for zero, which made advanced mathematics difficult.
Binary Origins
The binary number system was described by Gottfried Leibniz in the 17th century, but it wasn't widely used until the advent of computers in the 20th century. Leibniz saw spiritual significance in the binary system.
Different Bases Worldwide
While most cultures use base-10, some use other bases. The Yuki people of California used a base-8 system, counting the spaces between fingers rather than the fingers themselves. Some languages in Papua New Guinea use base-27!
Digital Everything
All digital information—text, images, sound, and video—is ultimately stored as binary numbers. A typical high-quality photo might contain millions of 1s and 0s representing the color of each pixel.
Decimal
Binary
Octal
Hexadecimal





