Numerical Expressions - Definition, Examples, Quiz, FAQ, Trivia
Understanding Math Expressions with Numbers and Operations
What is a Numerical Expression?

A numerical expression is a mathematical phrase that contains only numbers and operation symbols. Think of it as a math sentence that uses numbers instead of words!
Numerical expressions don't have an equal sign - that would make them an equation. They're just combinations of numbers and operations waiting to be calculated.
Math Fact!
Numerical expressions can include addition (+), subtraction (-), multiplication (× or *), and division (÷ or /). They can also include parentheses ( ) to show which operations to do first.
Examples of numerical expressions:
5 + 3
12 × 4
(10 - 2) ÷ 4
5² + 6
Numerical Expression vs Algebraic Expression

While both are mathematical expressions, there's an important difference between numerical and algebraic expressions:
Numerical Expressions
Contain only numbers and operations
8 + 4 × 3
(10 - 2) ÷ 4
Algebraic Expressions
Contain variables (like x, y) along with numbers and operations
x + 5
3y - 2
The key difference is that numerical expressions have specific values that can be calculated, while algebraic expressions represent relationships that can change depending on the variable values.
How to Evaluate Numerical Expressions
Evaluating a numerical expression means finding its value by performing the operations in the correct order. We use the order of operations, often remembered by the acronym PEMDAS:
Parentheses
Do operations inside parentheses first
Exponents
Calculate exponents (powers and roots)
Multiply & Divide
From left to right
Add & Subtract
From left to right
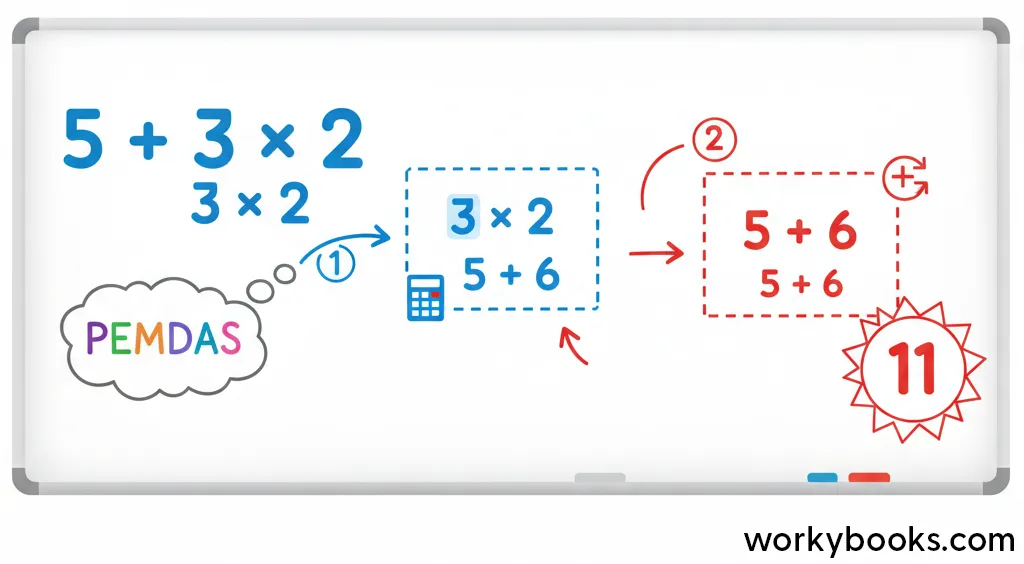
Let's evaluate an example: 5 + 3 × 2
Following PEMDAS, we do multiplication before addition:
3 × 2 = 6, then 5 + 6 = 11
So, 5 + 3 × 2 = 11
Examples of Numerical Expressions

Numerical expressions can be simple or complex. Here are some examples with different operations:
Simple Addition
7 + 9
Value: 16
With Multiplication
4 × 5 + 2
Value: 22
With Parentheses
(10 - 2) × 3
Value: 24
With Exponents
3² + 4
Value: 13
Fraction Form
½ + ⅓
Value: ⅚
These examples show how numerical expressions can combine different operations. Remember to always follow the order of operations (PEMDAS) when evaluating them!
Writing Numerical Expressions
We often need to write numerical expressions based on word descriptions or real-world situations. This is an important skill for solving math problems!
Identify Numbers
Find the numbers mentioned in the problem
Identify Operations
Determine which operations to use
Consider Order
Use parentheses if operations need to happen in a specific order
Write Expression
Combine numbers and operations to form the expression
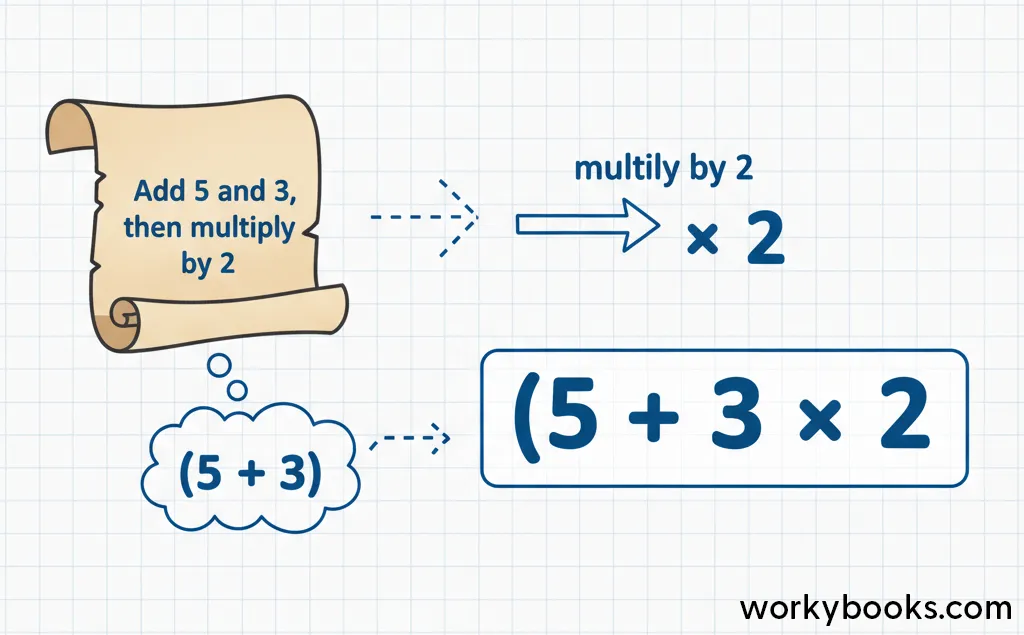
Example: Write a numerical expression for "Add 5 and 3, then multiply by 2"
Step 1: Numbers are 5, 3, and 2
Step 2: Operations are addition and multiplication
Step 3: Addition should happen first, so we need parentheses: (5 + 3)
Step 4: Multiply the result by 2: (5 + 3) × 2
Word Clues
Addition: sum, plus, total, more than
Subtraction: difference, minus, less than, take away
Multiplication: product, times, multiplied by
Division: quotient, divided by, split equally
Numerical Expressions Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about numerical expressions.
Frequently Asked Questions
Here are answers to some common questions about numerical expressions:
Math Facts About Numerical Expressions
Discover some fascinating facts about numerical expressions and mathematics!
Historical Symbols
The plus (+) and minus (-) signs first appeared in print in the late 15th century. The equals sign (=) was invented in 1557 by Welsh mathematician Robert Recorde, who said he chose two parallel lines because "no two things can be more equal."
Universal Language
Numerical expressions are almost a universal language! While spoken languages differ around the world, the mathematical symbols and operations in numerical expressions are understood by mathematicians everywhere, making math a truly global language.
PEMDAS Memory Aid
The mnemonic "Please Excuse My Dear Aunt Sally" (PEMDAS) has helped generations of students remember the order of operations. Some teachers now use "GEMDAS" where G stands for "Grouping symbols" instead of parentheses, to include brackets and braces.
Calculator Logic
Calculators and computers use the order of operations (PEMDAS) to evaluate numerical expressions. This is why you get different answers if you enter 5+3×2 on a basic calculator (which might calculate left to right) versus a scientific calculator (which follows PEMDAS).





