Obtuse Angles - Definition, Examples, Quiz, FAQ, Trivia
Learn about obtuse angles with easy explanations, visual examples, and practice activities
What is an Obtuse Angle?
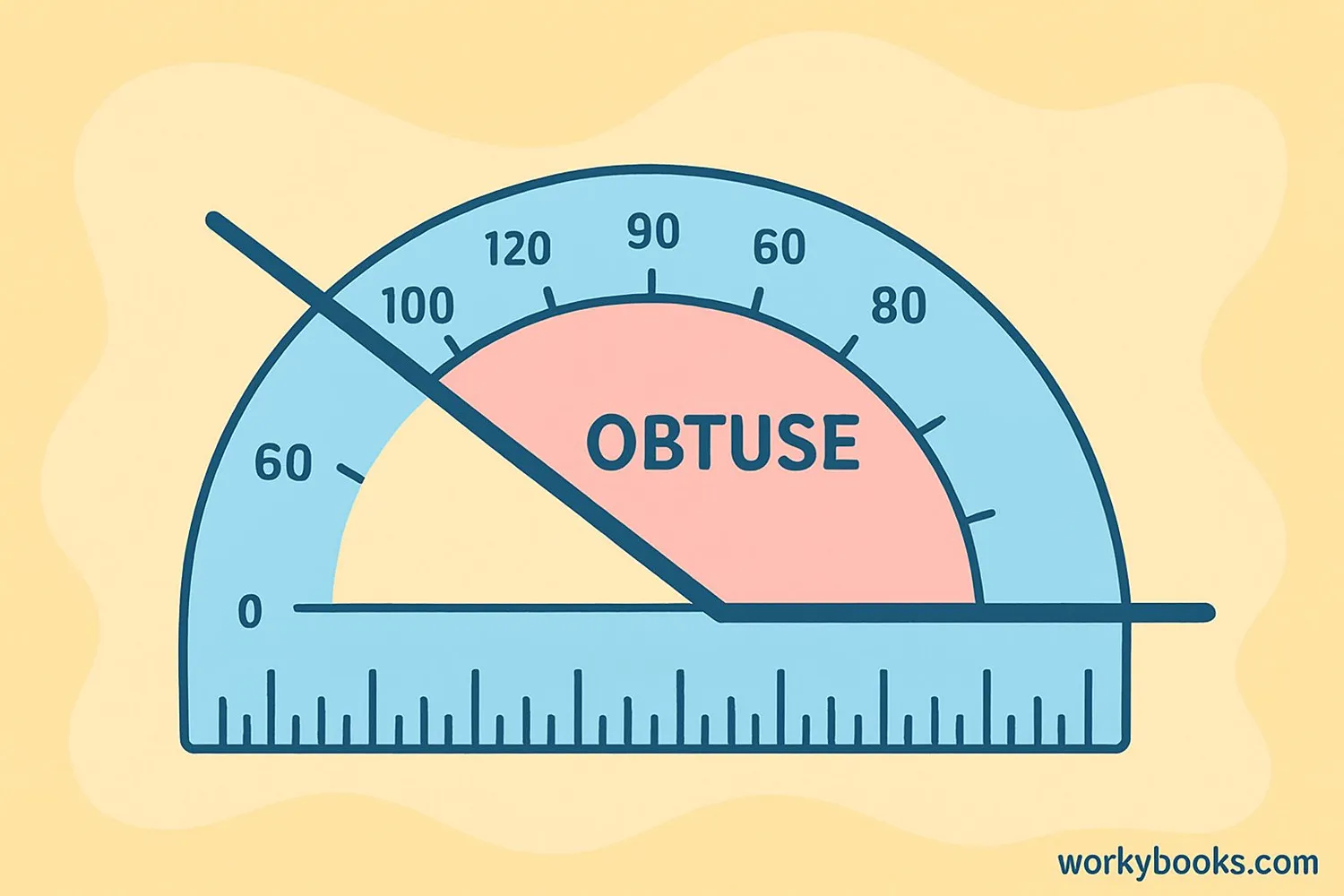
An obtuse angle is a type of angle that measures greater than 90 degrees but less than 180 degrees.
Think of it as a "wide" angle that opens more than a right angle (which is exactly 90°), but not as much as a straight angle (which is exactly 180°).
Key facts about obtuse angles:
- Measures between 90° and 180°
- Looks wider than a right angle
- Found in many everyday objects and shapes
- In a triangle, an obtuse angle means one angle is greater than 90°
Key Concept
An obtuse angle is larger than a right angle (90°) but smaller than a straight angle (180°).
Types of Angles
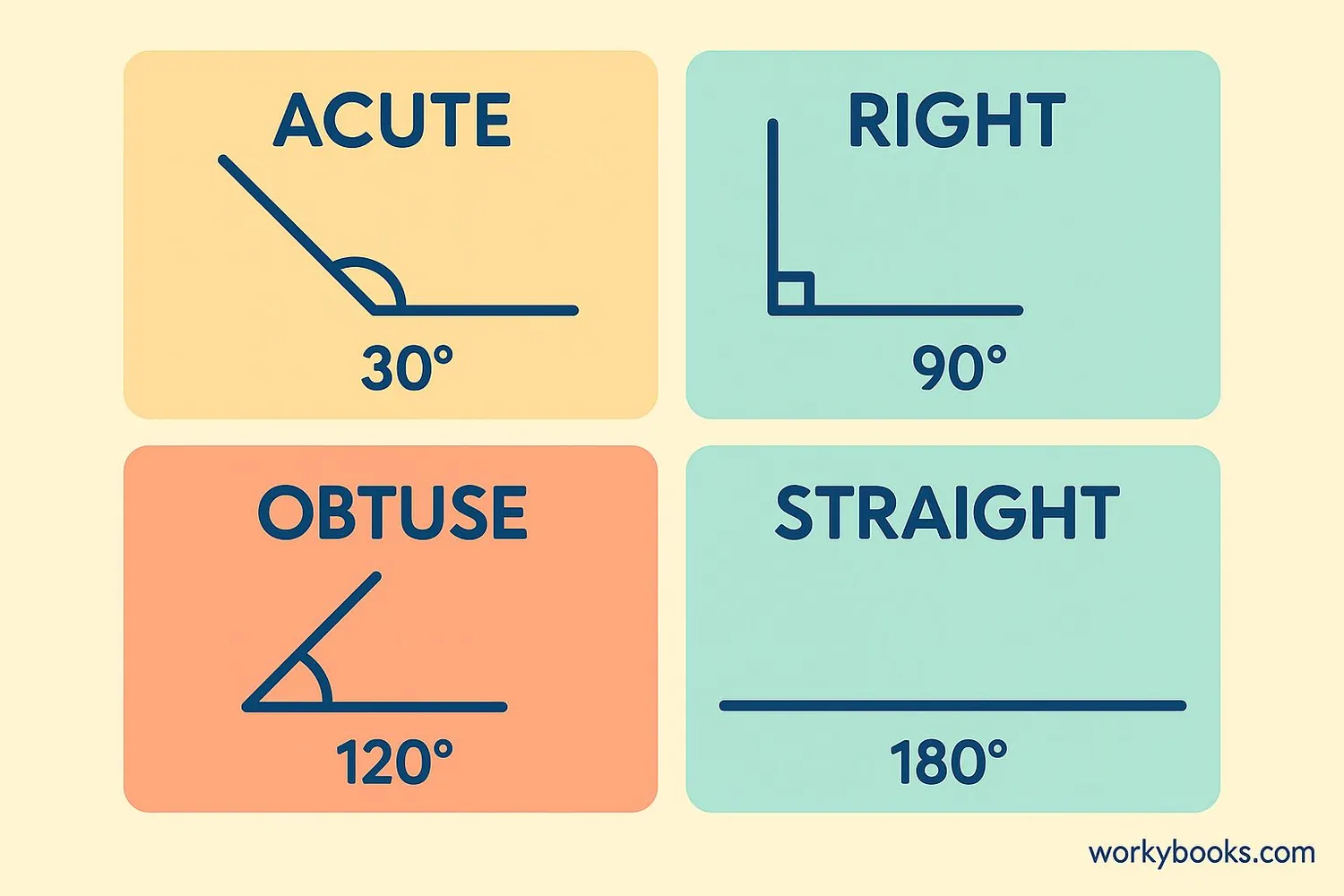
Understanding obtuse angles is easier when we compare them to other types of angles:
| Angle Type | Degree Measurement | Visual Description |
|---|---|---|
| Acute Angle | Less than 90° | A narrow, sharp angle |
| Right Angle | Exactly 90° | Forms a perfect "L" shape |
| Obtuse Angle | Between 90° and 180° | A wide, open angle |
| Straight Angle | Exactly 180° | A straight line |
Remember that obtuse angles are always wider than right angles but not as wide as straight angles. When you see an angle that looks "spread out," it's probably an obtuse angle!
Remember
Obtuse angles are the "big brothers" of acute angles - they're wider and more open!
How to Draw an Obtuse Angle
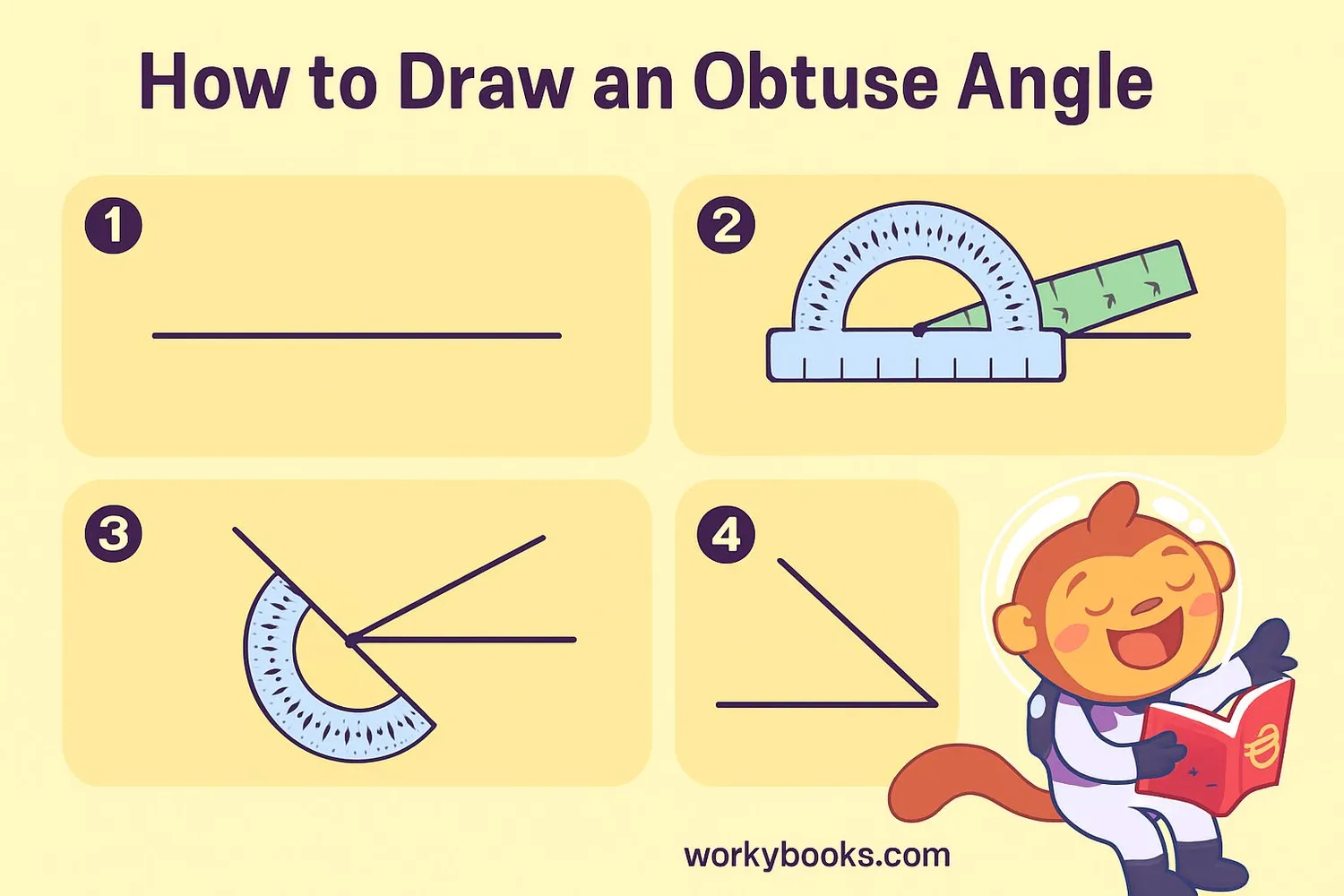
Drawing an obtuse angle is easy with a protractor. Follow these steps:
- Draw a straight line (this will be one side of your angle)
- Place the center of your protractor at one end of the line
- Find a point between 90° and 180° on the protractor
- Mark a dot at your chosen measurement (like 110°)
- Remove the protractor and draw a line from the endpoint to your dot
Protractor Tip
Remember: The bottom line of the protractor should align with your first line, and the center hole should be exactly at the endpoint.
- Draw a right angle first (like the corner of a book)
- Extend one side to make the angle wider
- Make sure it's wider than the right angle but doesn't form a straight line
Practice Tip
Try drawing obtuse angles of different sizes: 100°, 120°, 150°. Notice how they all have that "wide open" look!
Obtuse Angles in Real Life
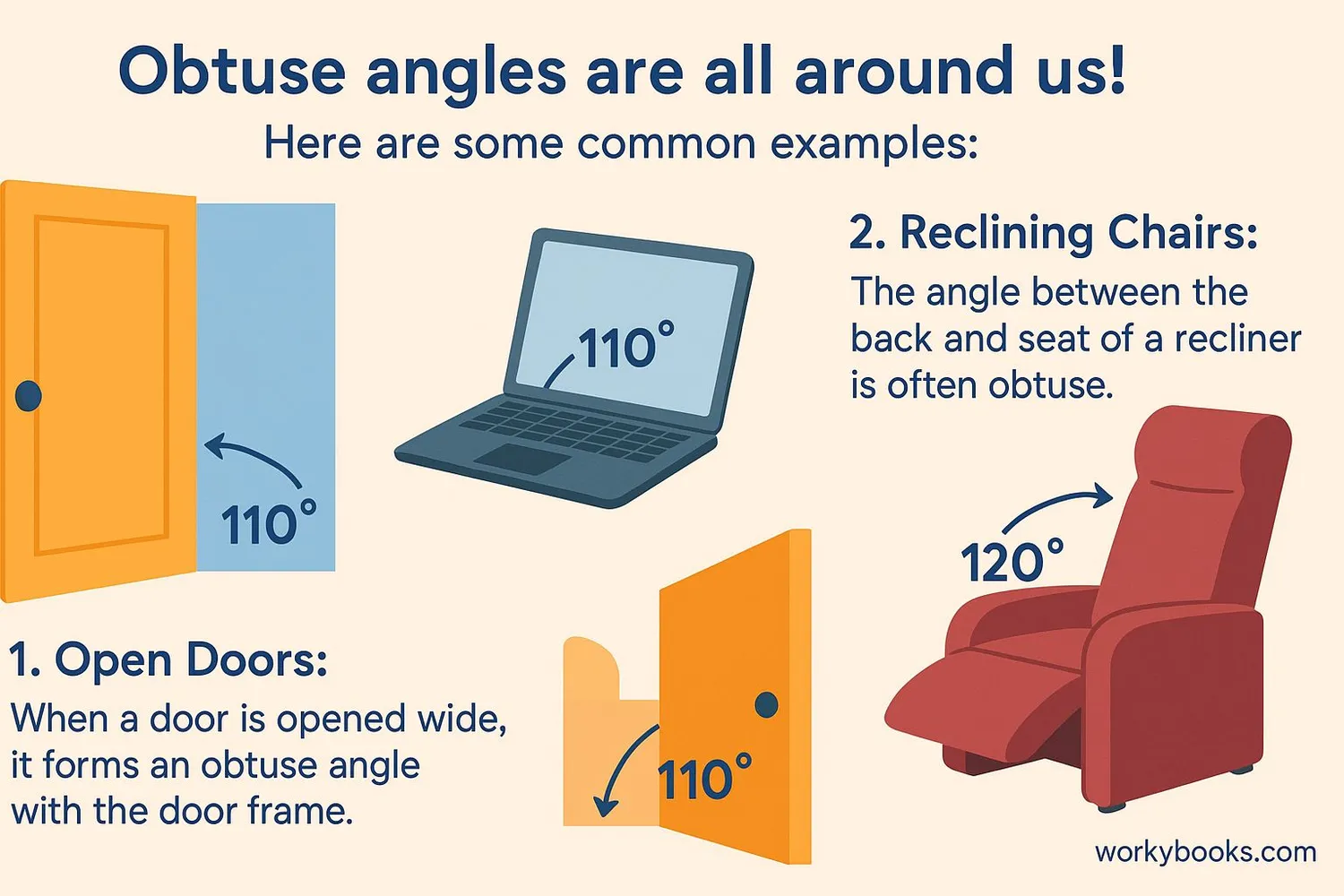
Obtuse angles are all around us! Here are some common examples:
1. Open Doors: When a door is opened wide, it forms an obtuse angle with the door frame.
2. Reclining Chairs: The angle between the back and seat of a recliner is often obtuse.
3. Spread Fingers: The angle between your thumb and index finger when you make a "L" shape is obtuse.
4. Roof Slopes: Many house roofs have obtuse angles where two slopes meet.
5. Open Books: When a book is lying open, the angle between its pages is obtuse.
Next time you're in your classroom or at home, look around and see how many obtuse angles you can find!
Observation Challenge
Can you find three obtuse angles in your classroom right now? Look at doors, windows, books, and furniture!
Obtuse Triangles
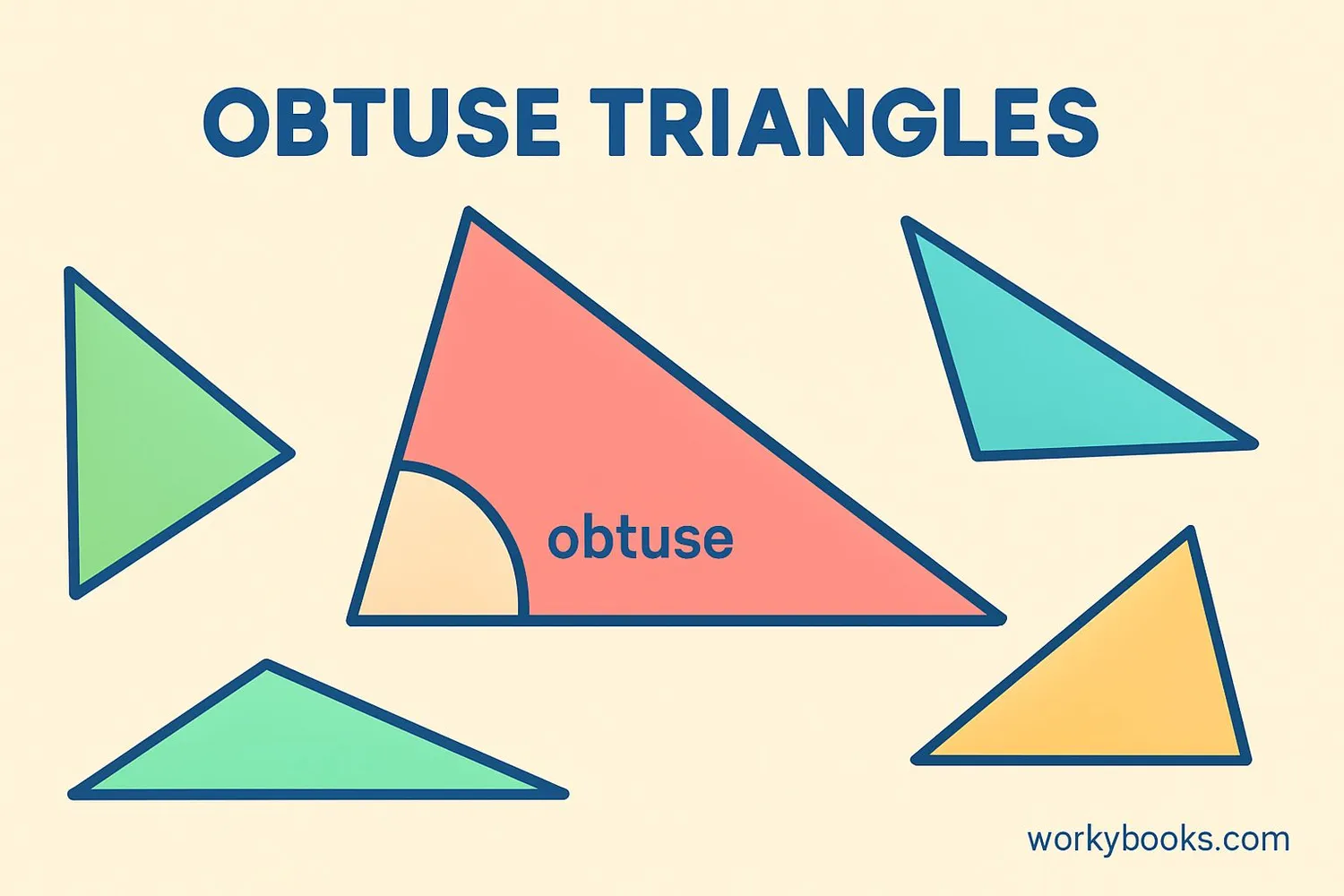
An obtuse triangle is a special type of triangle that has one obtuse angle (greater than 90°).
Since all angles in a triangle add up to 180°, if one angle is obtuse (say 120°), the other two angles must be acute (less than 90°).
Properties of obtuse triangles:
- Has exactly one angle greater than 90°
- The other two angles are acute (less than 90°)
- The longest side is opposite the obtuse angle
- Can be scalene (all sides different) or isosceles (two sides equal)
Angle Sum Property
In any triangle, the sum of all three interior angles always equals 180°.
Triangle Tip
If a triangle has one obtuse angle, it can never have a right angle too, because 90° + 91° = 181° which is already more than 180°!
Obtuse Angle Quiz
Test your knowledge about obtuse angles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about obtuse angles:
Angle Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Measurement
The Babylonians developed the first angle measurement system over 4,000 years ago using a base-60 number system, which is why we have 360 degrees in a circle today.
Nature's Angles
Honeybees build honeycombs with hexagonal cells that have 120° angles - which are obtuse! This shape allows them to store the most honey using the least wax.
Architecture Angles
The Leaning Tower of Pisa leans at an angle of about 4 degrees. While this is acute, the obtuse angles formed between the tower and the ground are crucial to its stability.
Sports Angles
In basketball, players shoot at different angles to score. The optimal shooting angle is about 45°-50° (acute), but bank shots often use obtuse angles against the backboard.





