Octagonal Prism - Definition, Examples, Quiz, FAQ, Trivia
Understanding 3D Shapes and Geometry
What is an Octagonal Prism?
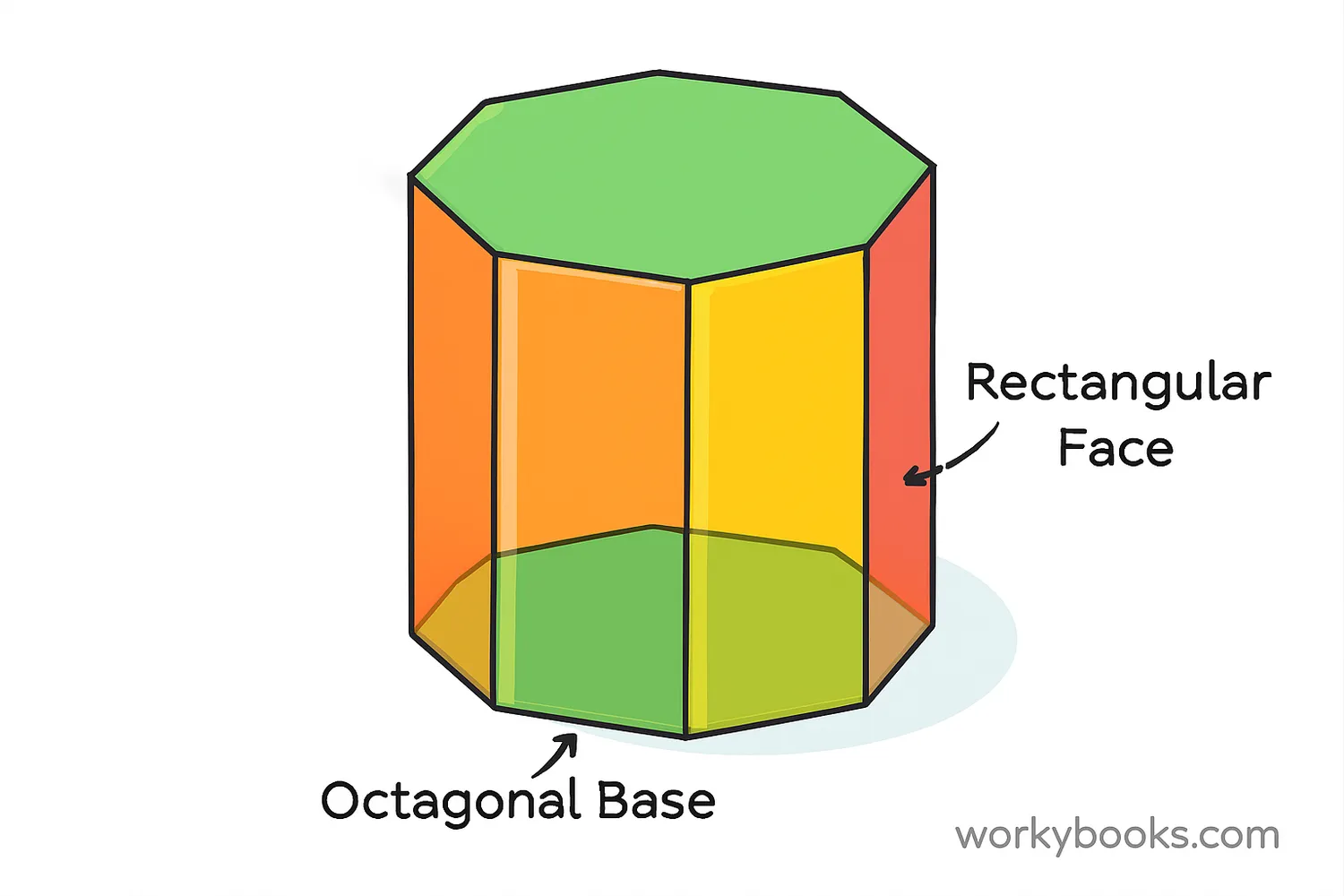
An octagonal prism is a three-dimensional shape that has two octagonal bases and eight rectangular faces connecting them. Think of it like a box with octagon-shaped ends!
The word "octagonal" comes from "octagon," which means an eight-sided shape. A prism is a solid shape with identical ends and flat sides. So an octagonal prism has two octagon ends and rectangular sides connecting them.
Math Fact!
An octagonal prism has 10 faces, 24 edges, and 16 vertices (corners). Can you count them all?
Properties of an Octagonal Prism
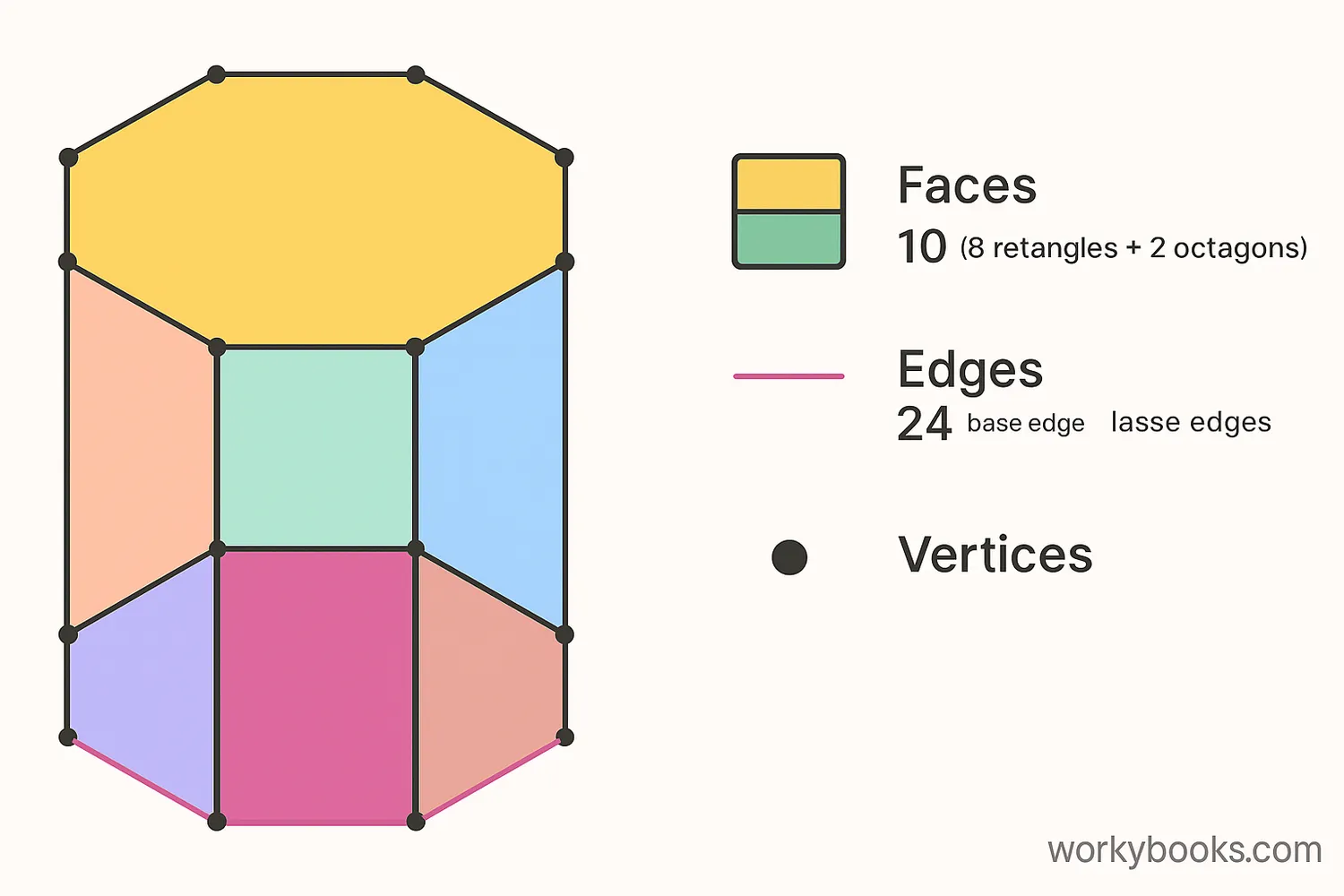
Every octagonal prism has specific properties that make it unique. Here are the key characteristics:
Faces
10 faces total: 2 octagonal bases + 8 rectangular sides
Edges
24 edges where faces meet
Vertices
16 vertices (corner points)
Symmetry
Has rotational symmetry around its central axis
Parallel Bases
The two octagonal bases are parallel and congruent
When all the rectangular faces are perpendicular to the bases, we call it a right octagonal prism. If the faces are slanted, it's called an oblique octagonal prism.
Volume of an Octagonal Prism
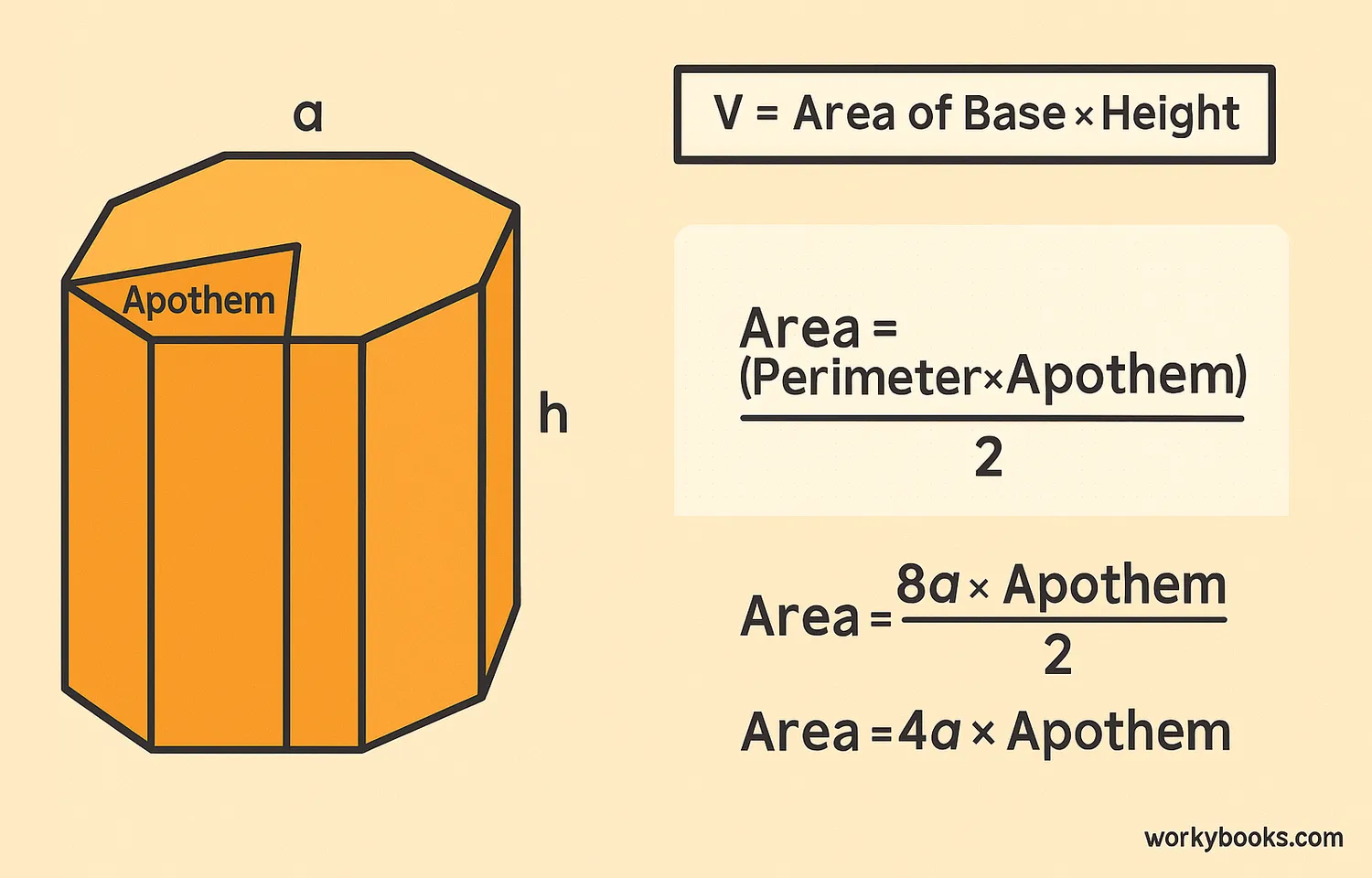
The volume of an octagonal prism tells us how much space is inside the shape. To find it, we use this formula:
First, we need to find the area of the octagonal base. If we know the side length (a) of the octagon, we can use this formula:
Then we multiply this area by the height of the prism to get the volume. The height is the distance between the two octagonal bases.
Example Calculation
If an octagonal prism has side length 4 cm and height 10 cm:
Area of octagon = 2 × (1 + √2) × 4² ≈ 77.25 cm²
Volume = 77.25 × 10 = 772.5 cm³
Surface Area of an Octagonal Prism
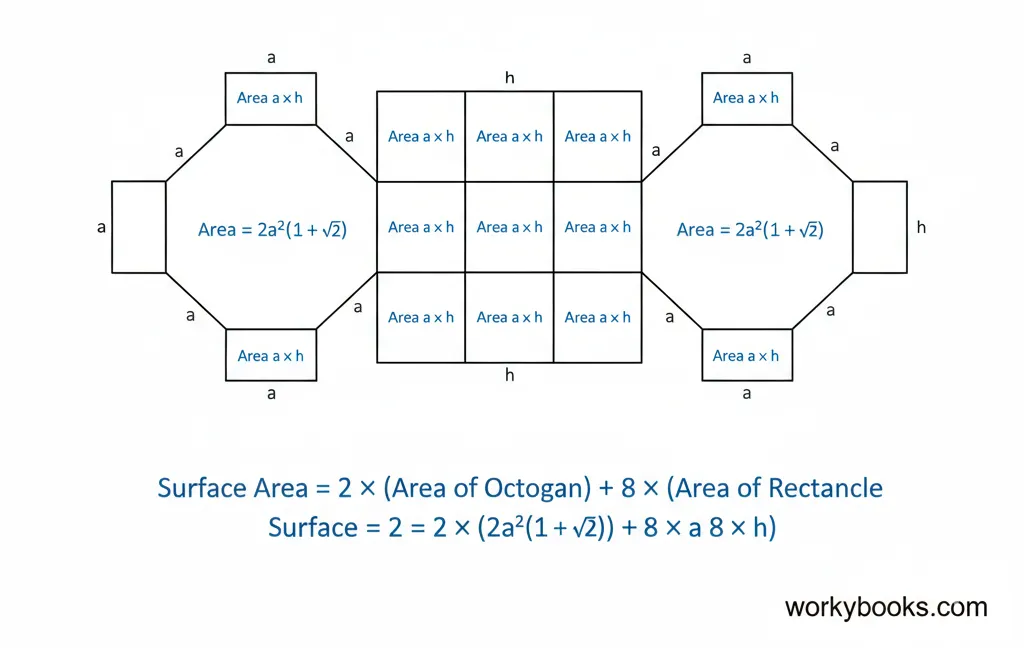
The surface area of an octagonal prism is the total area of all its faces. To find it, we add the areas of the two octagonal bases and the eight rectangular sides.
The area of each rectangle is simply the side length of the octagon multiplied by the height of the prism. So if we know the side length (a) and height (h):
This formula might look complicated, but it's just adding up all the faces. The first part calculates the area of the two octagons, and the second part calculates the area of the eight rectangles.
Example Calculation
If an octagonal prism has side length 3 cm and height 8 cm:
Area of one octagon = 2 × (1 + √2) × 3² ≈ 43.46 cm²
Area of two octagons = 2 × 43.46 = 86.92 cm²
Area of one rectangle = 3 × 8 = 24 cm²
Area of eight rectangles = 8 × 24 = 192 cm²
Total Surface Area = 86.92 + 192 = 278.92 cm²
Octagonal Prism Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about octagonal prisms.
Frequently Asked Questions
Here are answers to some common questions about octagonal prisms:
Math Facts About Octagonal Prisms
Discover some fascinating facts about octagonal prisms and geometry!
Architectural Marvel
The famous Flatiron Building in New York City has a distinctive triangular shape that's actually a modified octagonal prism. Its unique design makes it one of the most photographed buildings in the world!
Crystal Structures
Some minerals and crystals naturally form octagonal prism shapes. The mineral prismatine, for example, often crystallizes as elongated octagonal prisms that can be several inches long!
Mathematical Pattern
If you look at the number of faces, edges, and vertices of an octagonal prism (10, 24, 16), they follow Euler's formula: F + V - E = 2. Check it: 10 + 16 - 24 = 2!
Historical Use
Ancient Roman and Greek architects often used octagonal prisms for decorative columns and pillars. The eight-sided shape provided structural stability while creating visual interest.





