Octal Number System - Definition, Examples, Quiz, FAQ, Trivia
Understanding Base-8 Counting for Young Mathematicians
What is the Octal Number System?

The octal number system is a way of counting that uses only eight digits: 0, 1, 2, 3, 4, 5, 6, and 7. It's called "octal" because "oct" means eight, just like an octopus has eight legs!
We usually use the decimal system (base-10) with ten digits (0-9). But in octal, when we reach 7, the next number is 10 (which is eight in decimal). It's like counting on your fingers but stopping at eight instead of ten!
Math Fact!
The octal number system is a base-8 system, which means each place value represents a power of 8 (ones, eights, sixty-fours, etc.).
| Decimal (Base-10) | Octal (Base-8) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
How the Octal Number System Works
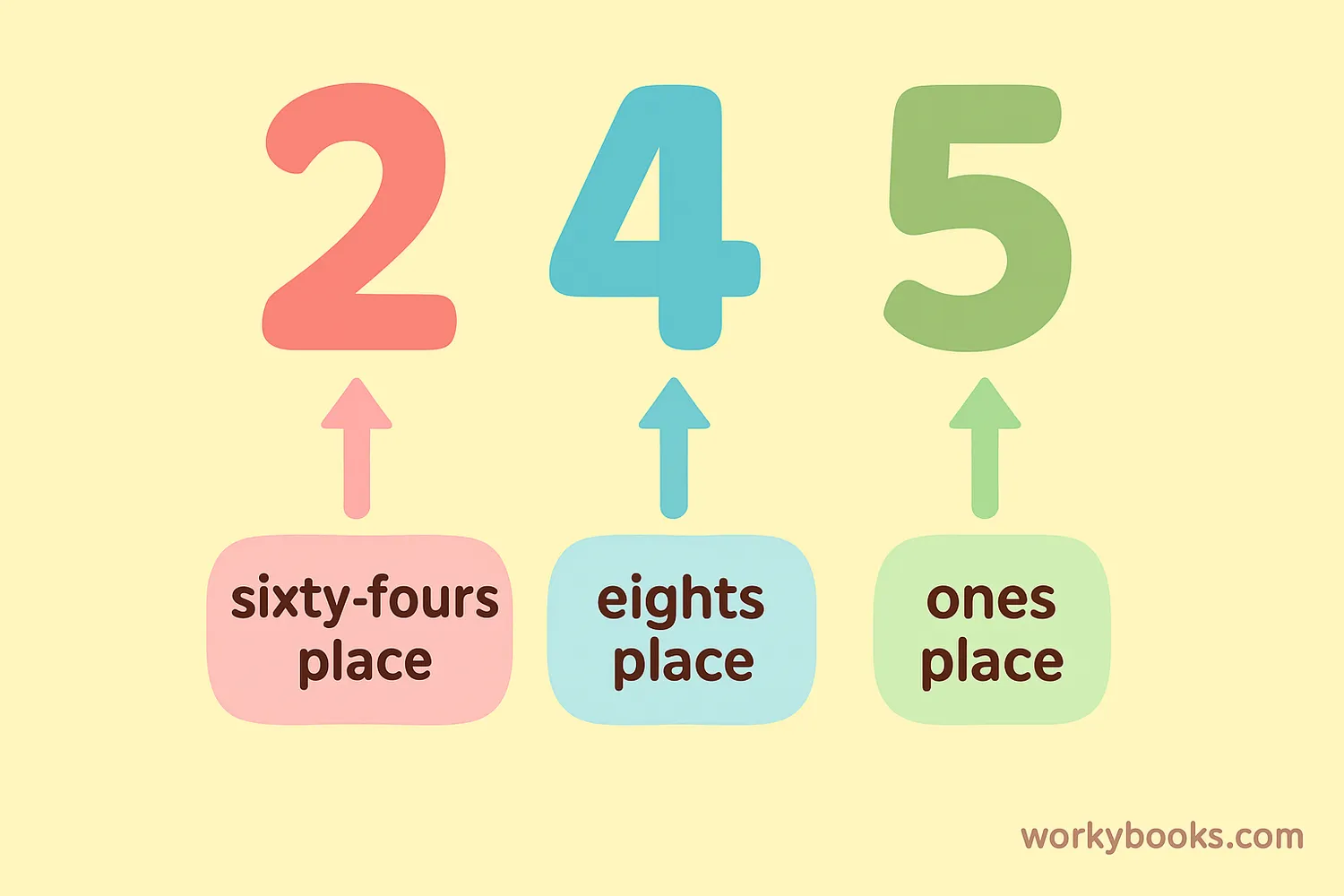
Just like in our regular decimal system, each digit in an octal number has a place value. But instead of ones, tens, hundreds (powers of 10), octal uses ones, eights, sixty-fours (powers of 8):
Ones Place
80 = 1 (any number to the power of 0 is 1)
Eights Place
81 = 8 (eight to the power of 1 is 8)
Sixty-Fours Place
82 = 64 (eight to the power of 2 is 64)
Five-Hundred-Twelves Place
83 = 512 (eight to the power of 3 is 512)
So when we see an octal number like 245, it means:
2 sixty-fours + 4 eights + 5 ones
Let's calculate that: (2 × 64) + (4 × 8) + (5 × 1) = 128 + 32 + 5 = 165 in decimal!
Example: Reading Octal Numbers
The octal number 123 means:
1 sixty-four (1 × 64) + 2 eights (2 × 8) + 3 ones (3 × 1) = 64 + 16 + 3 = 83 in decimal
Octal to Decimal Conversion
Converting octal numbers to decimal is like solving a puzzle! Here's how you can do it step by step:
Conversion Steps
- Write down the octal number
- Label each digit with its place value (starting from the right)
- Multiply each digit by its place value (power of 8)
- Add up all the results
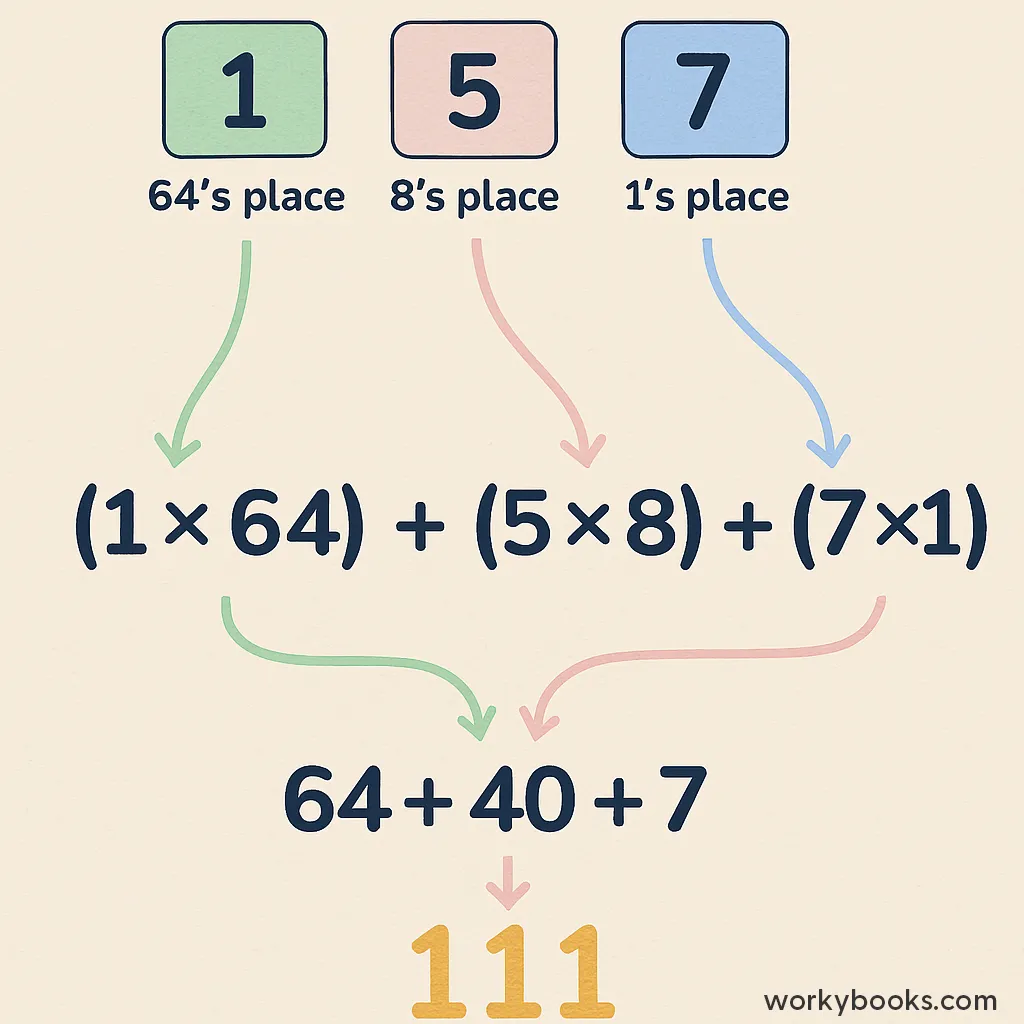
Example: Convert octal 157 to decimal
Step 1: Write the number: 157
Step 2: Label place values from right to left:
7 → ones place (80 = 1)
5 → eights place (81 = 8)
1 → sixty-fours place (82 = 64)
Step 3: Multiply each digit by its place value:
1 × 64 = 64
5 × 8 = 40
7 × 1 = 7
Step 4: Add the results: 64 + 40 + 7 = 111
So, octal 157 = decimal 111
Practice Tip!
Try converting these octal numbers to decimal: 10, 25, 77. Check your answers: 10₈ = 8₁₀, 25₈ = 21₁₀, 77₈ = 63₁₀.
Octal Addition
Adding octal numbers is similar to adding decimal numbers, but we carry over when our sum reaches 8 (instead of 10). Let's learn how:
Add Ones Place
Add the rightmost digits. If the sum is 8 or more, carry over to the eights place.
Add Eights Place
Add the next digits plus any carry from the ones place.
Continue Left
Keep adding each place value, carrying when sums reach 8 or more.
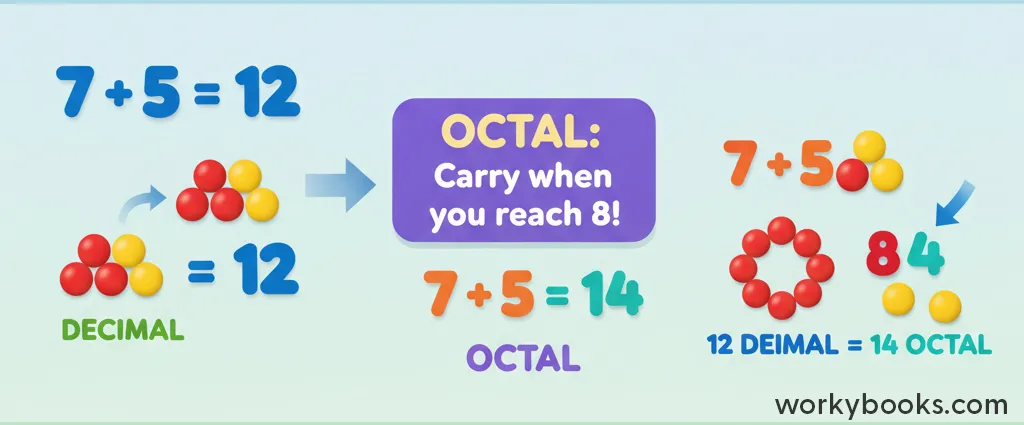
Example: Add 25₈ + 17₈
Step 1: Add ones place: 5 + 7 = 12 (but 12 is more than 7, so in octal we carry)
12 in decimal = 14 in octal (because 1 eight and 4 ones)
Write down 4 in ones place, carry 1 to eights place
Step 2: Add eights place: 2 + 1 + 1 (carry) = 4
Step 3: Write the result: 44₈
Let's check: 25₈ = 21₁₀, 17₈ = 15₁₀, 21 + 15 = 36₁₀
36₁₀ in octal is 44₈ (4 eights + 4 ones = 32 + 4 = 36) ✓
Remember, the biggest digit in octal is 7, so whenever your sum is 8 or more, you need to carry over to the next place value!
Octal Number System Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about the octal number system.
Frequently Asked Questions
Here are answers to some common questions about the octal number system:
Math Facts About the Octal System
Discover some fascinating facts about the octal number system and number systems in general!
Historical Use
Some Native American tribes used octal counting systems because they counted the spaces between their fingers rather than the fingers themselves!
Computer Connection
Early computers often used groups of 12 or 24 bits, which worked well with octal because they're divisible by 3. This made octal a natural choice for representing binary numbers.
Easy Conversion
Converting between binary and octal is simple! Just group binary digits into sets of three (starting from the right) and convert each group to its octal equivalent.
Interesting Pattern
In octal, the number 77 is the largest two-digit number, just like 99 is in decimal. 77₈ equals 63₁₀, which is 7×8 + 7 = 56 + 7 = 63.





