Odd Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn about odd numbers with easy explanations, examples, and practice activities
What are Odd Numbers?

Odd numbers are numbers that cannot be divided into two equal groups. When you try to divide an odd number by 2, there's always one left over.
Think of it like this: if you have an odd number of cookies and try to share them equally between two friends, one cookie will always be left over. That's what makes it odd!
Examples of odd numbers: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21...
You can always tell if a number is odd by looking at its last digit. If it ends with 1, 3, 5, 7, or 9, it's an odd number!
Key Concept
Odd numbers end with 1, 3, 5, 7, or 9. When divided by 2, they always have a remainder of 1.
Properties of Odd Numbers
Odd numbers have special properties when we add, subtract, multiply, or divide them. Let's explore:
Addition Properties
• Odd + Odd = Even (3 + 5 = 8)
• Odd + Even = Odd (3 + 4 = 7)
• Even + Odd = Odd (4 + 3 = 7)
Subtraction Properties
• Odd - Odd = Even (7 - 3 = 4)
• Odd - Even = Odd (7 - 2 = 5)
• Even - Odd = Odd (8 - 3 = 5)
Multiplication Properties
• Odd × Odd = Odd (3 × 5 = 15)
• Odd × Even = Even (3 × 4 = 12)
• Even × Odd = Even (4 × 3 = 12)
Remember
When you multiply two odd numbers, the result is always odd. This is a special property that helps us solve many math problems!
Consecutive Odd Numbers

Consecutive odd numbers are odd numbers that come one after another in order, with no even numbers between them. They always have a difference of 2.
Examples:
3, 5, 7, 9, 11...
15, 17, 19, 21...
101, 103, 105, 107...
Notice how each number is 2 more than the one before it? That's what makes them consecutive odd numbers!
Consecutive odd numbers are useful in many math problems, especially when we need to find patterns or solve equations.
Pattern Tip
To find the next consecutive odd number, just add 2 to the current number!
Composite Odd Numbers
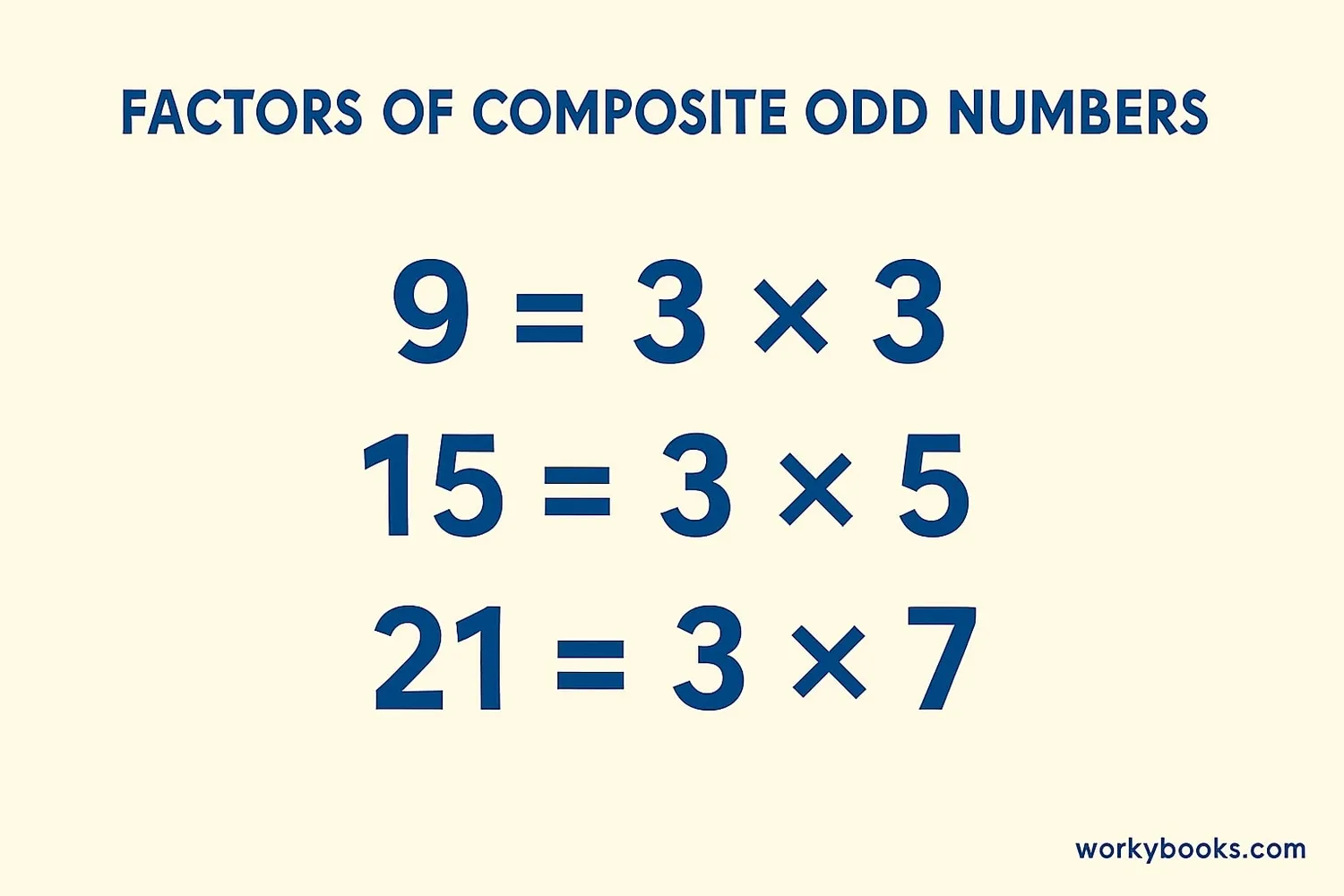
Composite numbers are numbers that have more than two factors. When these numbers are also odd, we call them composite odd numbers.
Examples of composite odd numbers:
• 9 (factors: 1, 3, 9)
• 15 (factors: 1, 3, 5, 15)
• 21 (factors: 1, 3, 7, 21)
• 25 (factors: 1, 5, 25)
• 27 (factors: 1, 3, 9, 27)
The smallest composite odd number is 9. Notice that 1 is not considered composite because it only has one factor (itself).
Composite odd numbers are important in math because they help us understand how numbers are built from smaller numbers (factors).
Remember
Not all odd numbers are prime! Composite odd numbers have more than two factors, while prime odd numbers have exactly two factors.
Negative Odd Numbers

Negative numbers can also be odd! Negative odd numbers are the opposites of positive odd numbers. They have the same properties as positive odd numbers but are less than zero.
Examples of negative odd numbers:
-1, -3, -5, -7, -9, -11, -13...
Just like positive odd numbers, negative odd numbers:
• Cannot be divided evenly by 2
• End with 1, 3, 5, 7, or 9 (in the ones place)
• Follow the same addition and multiplication rules
For example:
• (-3) + (-5) = -8 (even)
• (-3) × (-5) = 15 (odd)
Negative odd numbers are used in more advanced math and in real-world situations like temperatures below zero or debt calculations.
Pattern Tip
The pattern for negative odd numbers is the same as positive odd numbers, just on the negative side of the number line!
Odd Numbers Quiz
Test your knowledge with this quiz about odd numbers. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about odd numbers:
Math Trivia
Discover interesting facts about numbers:
Ancient Number Systems
The concept of odd and even numbers dates back to ancient Greece. Pythagoras and his followers considered odd numbers masculine and even numbers feminine.
The Sum of Odds
If you add consecutive odd numbers starting from 1, you always get a perfect square! For example: 1 = 1², 1+3 = 4 = 2², 1+3+5 = 9 = 3², and so on.
Prime Oddities
All prime numbers except 2 are odd numbers. This makes 2 the only even prime number in existence!
Largest Known Prime
The largest known prime number as of 2023 has over 24 million digits! It's an odd number, since all primes greater than 2 are odd.





