Operations on Rational Numbers - Definition, Examples, Quiz, FAQ, Trivia
Let's learn how to add, subtract, multiply, and divide rational numbers together!
What are Rational Numbers?
Hello! Think of a rational number as any number that can be written as a fraction, where the top number (numerator) and bottom number (denominator) are whole numbers, and the bottom number isn't zero.
That means numbers like ½, -¾, and even 5 (because you can write it as 5/1) are all rational numbers. Decimals that stop (like 0.25) or repeat in a pattern (like 0.333...) are also rational numbers!

Adding Rational Numbers
When you want to add two fractions, the most important rule is that they must have the same denominator (the bottom number). If they don't, you have to find a "common denominator."
Example: Let's add ⅓ + ½
- Find a common denominator: The smallest number that both 3 and 2 can divide into is 6.
- Rewrite the fractions: To turn ⅓ into sixths, you multiply top and bottom by 2 to get 2/6. To turn ½ into sixths, you multiply top and bottom by 3 to get 3/6.
- Add the numerators: Now just add the top numbers: 2 + 3 = 5.
- The answer is 5/6!
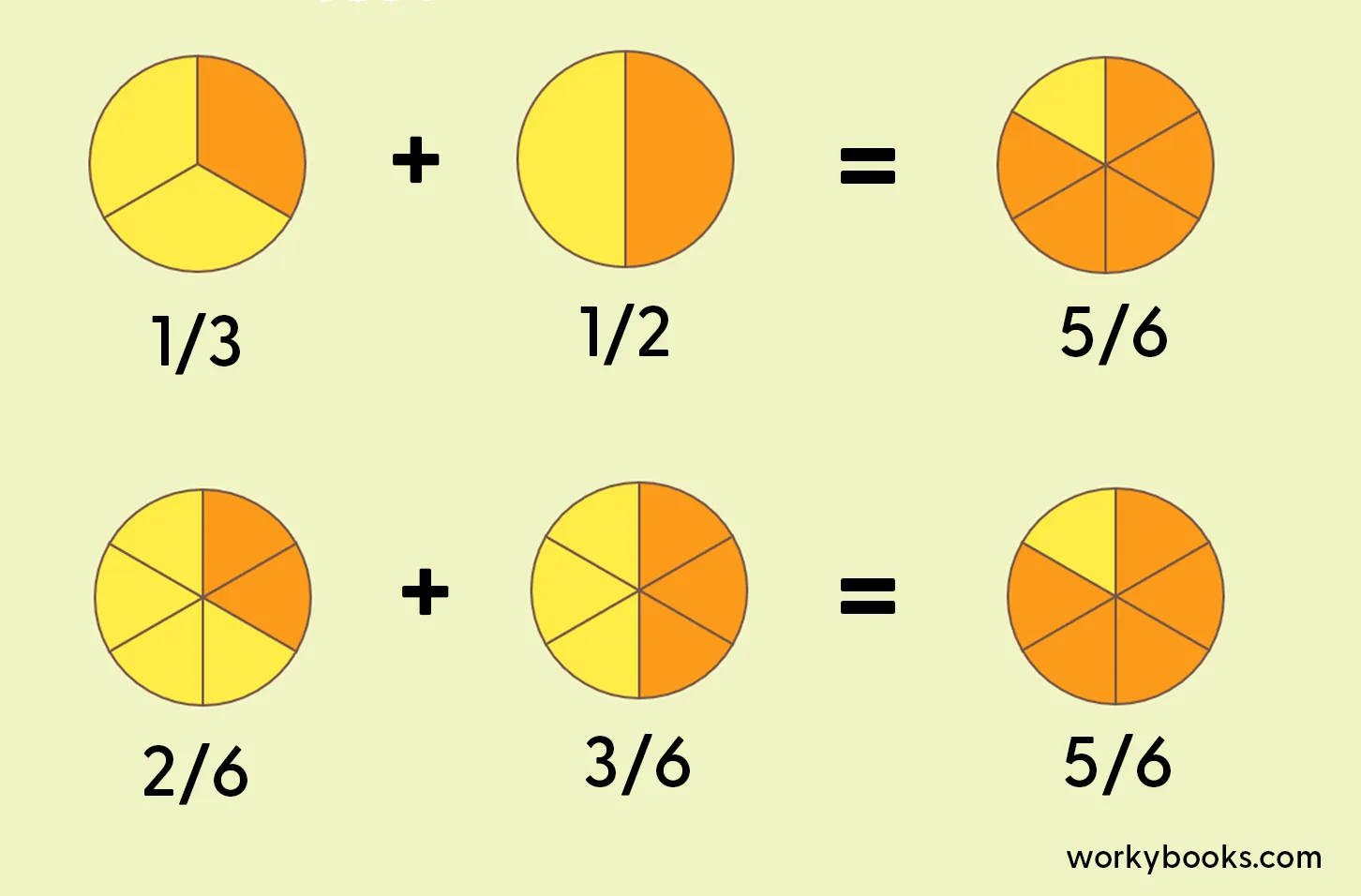
Subtracting Rational Numbers
Subtracting fractions works just like adding them! You need to have a common denominator before you can do anything.
Example: Let's subtract ¾ - ⅓
- Find a common denominator: The smallest number that both 4 and 3 can divide into is 12.
- Rewrite the fractions: Rewrite ¾ as 9/12 (multiply by 3). Rewrite ⅓ as 4/12 (multiply by 4).
- Subtract the numerators: Now subtract the top numbers: 9 - 4 = 5.
- The answer is 5/12!
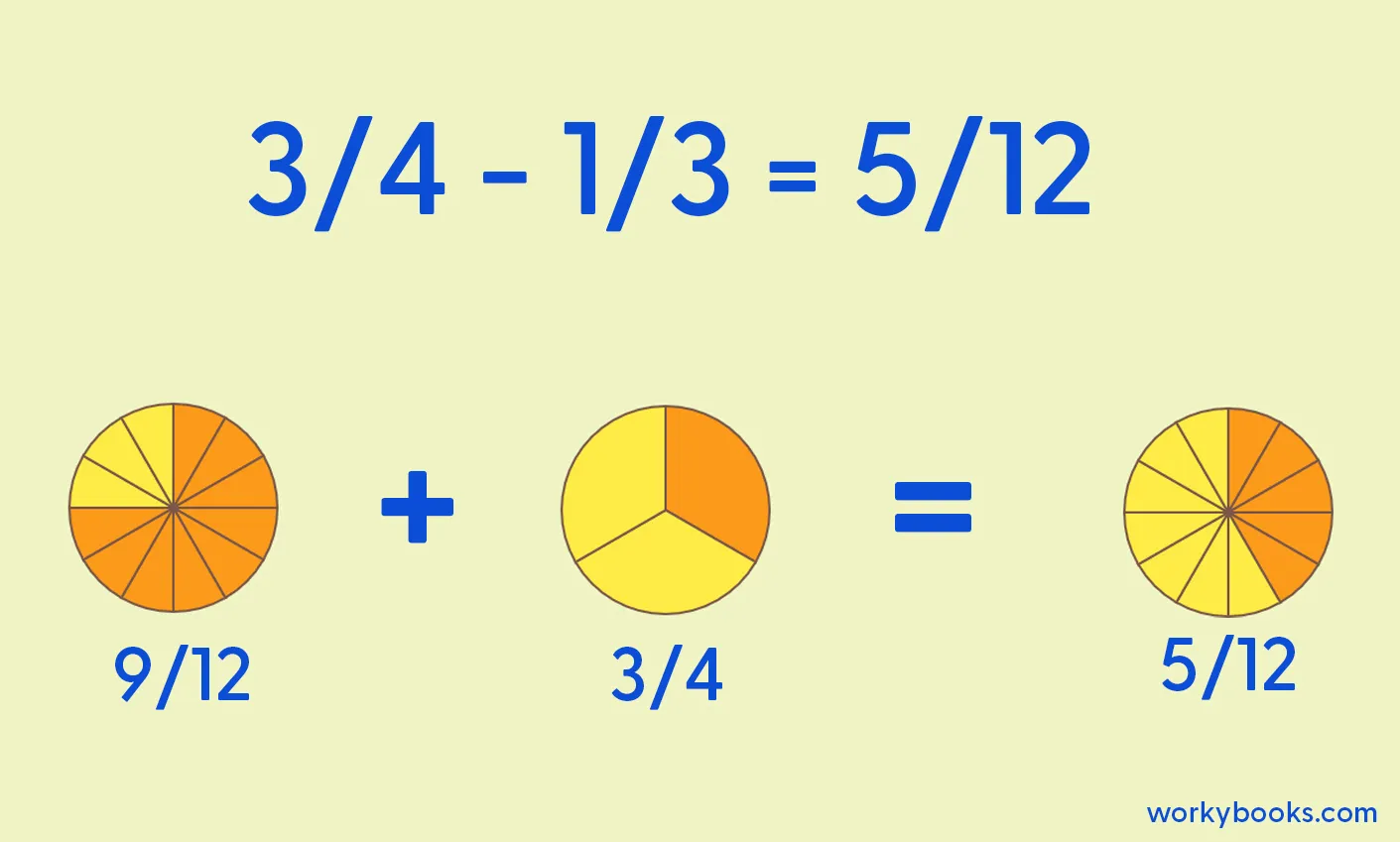
Multiplying Rational Numbers
Good news! Multiplying fractions is the easiest operation of all. You don't need a common denominator.
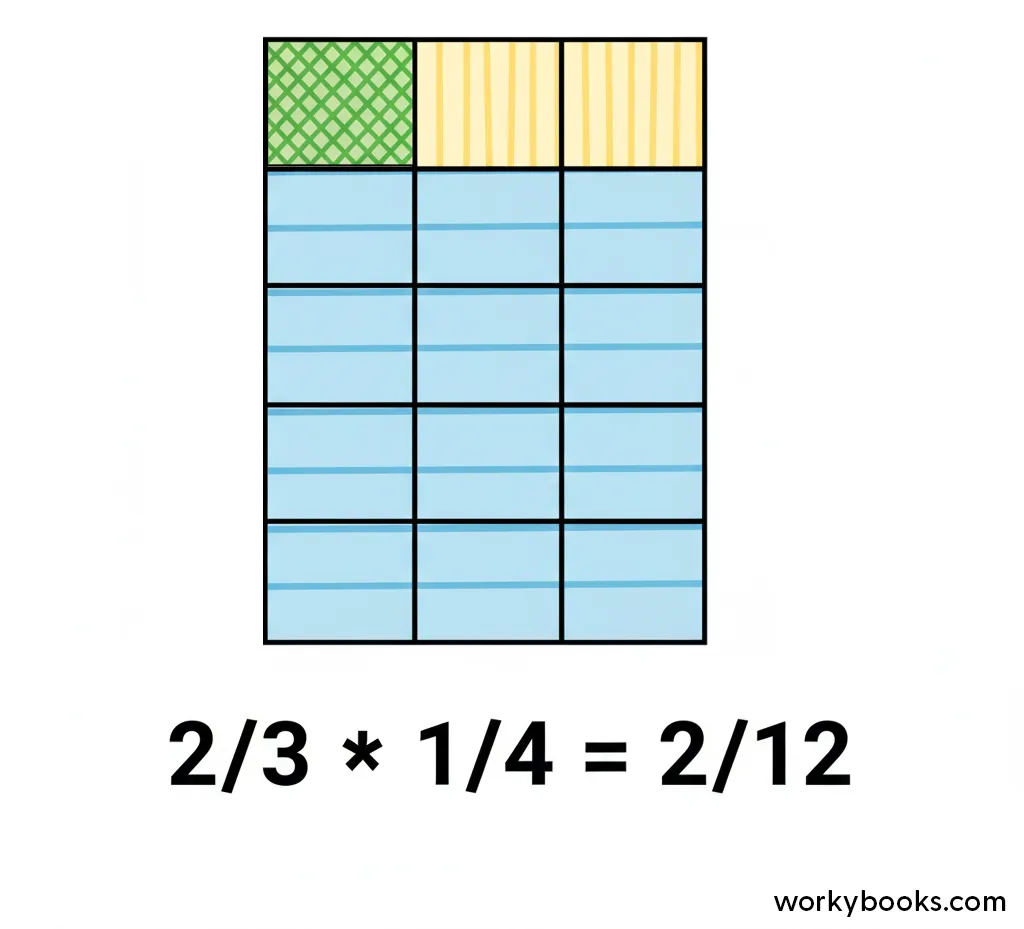
Example: Let's multiply ⅔ × ¼
- Multiply the numerators: Multiply the top numbers straight across: 2 × 1 = 2.
- Multiply the denominators: Multiply the bottom numbers straight across: 3 × 4 = 12.
- The answer is 2/12. You can simplify this to 1/6!
Dividing Rational Numbers
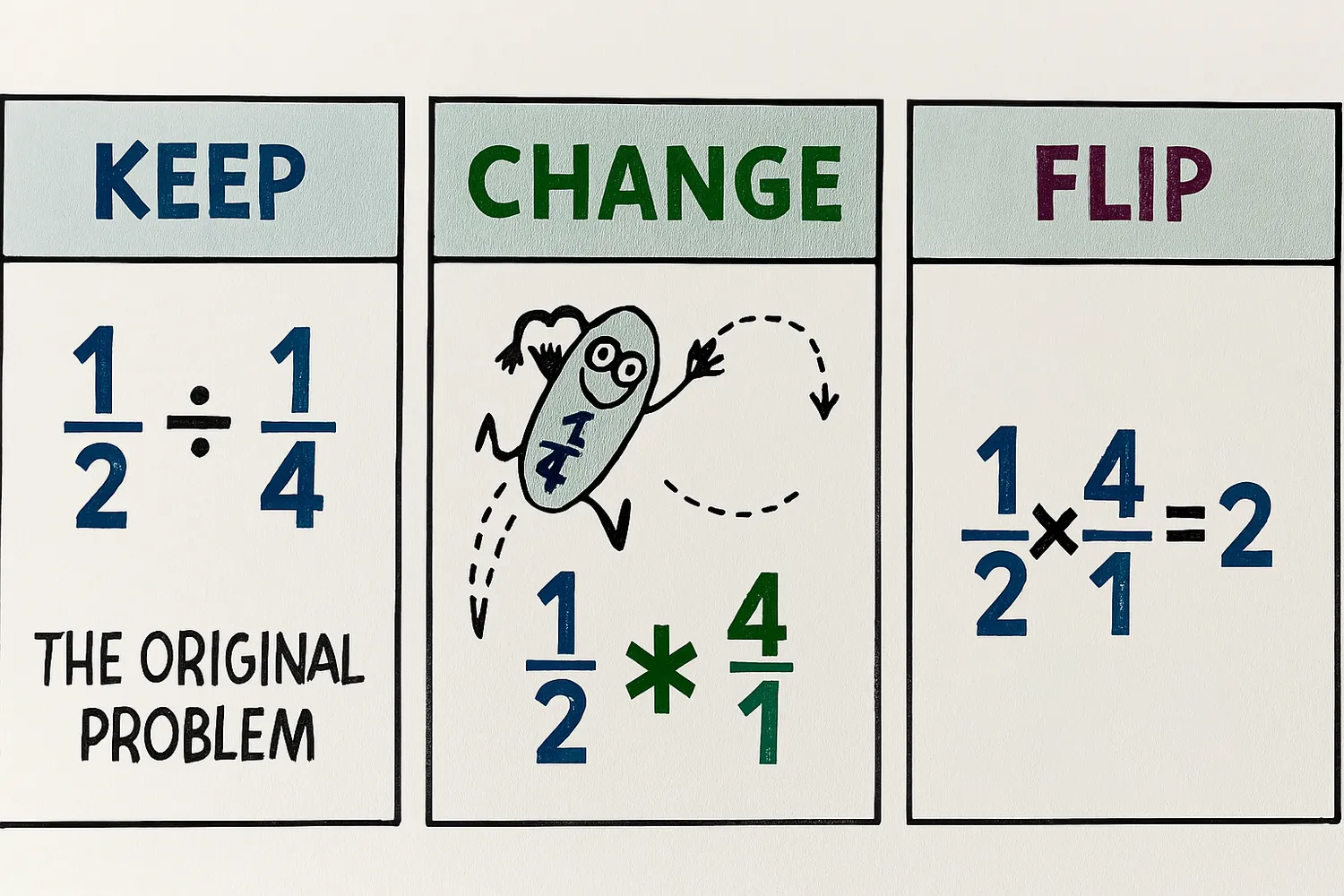
Dividing fractions seems tricky, but there's a simple three-step trick called "Keep, Change, Flip."
Example: Let's divide ½ ÷ ¼
- KEEP the first fraction: ½
- CHANGE the division sign to multiplication: ×
- FLIP the second fraction (this is called the reciprocal): ¼ becomes 4/1.
- Now multiply: ½ × 4/1 = 4/2, which simplifies to 2!
Quiz Time!
Test your knowledge! Choose the best answer for each question.
Frequently Asked Questions
Math Trivia
It's all about Ratios
The word "rational" in rational numbers comes from the word "ratio." A fraction is just a way of showing the ratio between two numbers!
Repeating Decimals
Even decimals that repeat forever, like 0.333..., are rational numbers because they can be written as a simple fraction (1/3).
Ancient Math
The ancient Egyptians were experts with fractions over 3,000 years ago! They mostly used "unit fractions," which are fractions with a 1 on top (like 1/2, 1/3, 1/4).


