Parallel Lines in Geometry - Definition, Examples, Quiz, FAQ, Trivia
Learn about parallel lines with visual examples, properties, and interactive activities
What are Parallel Lines?
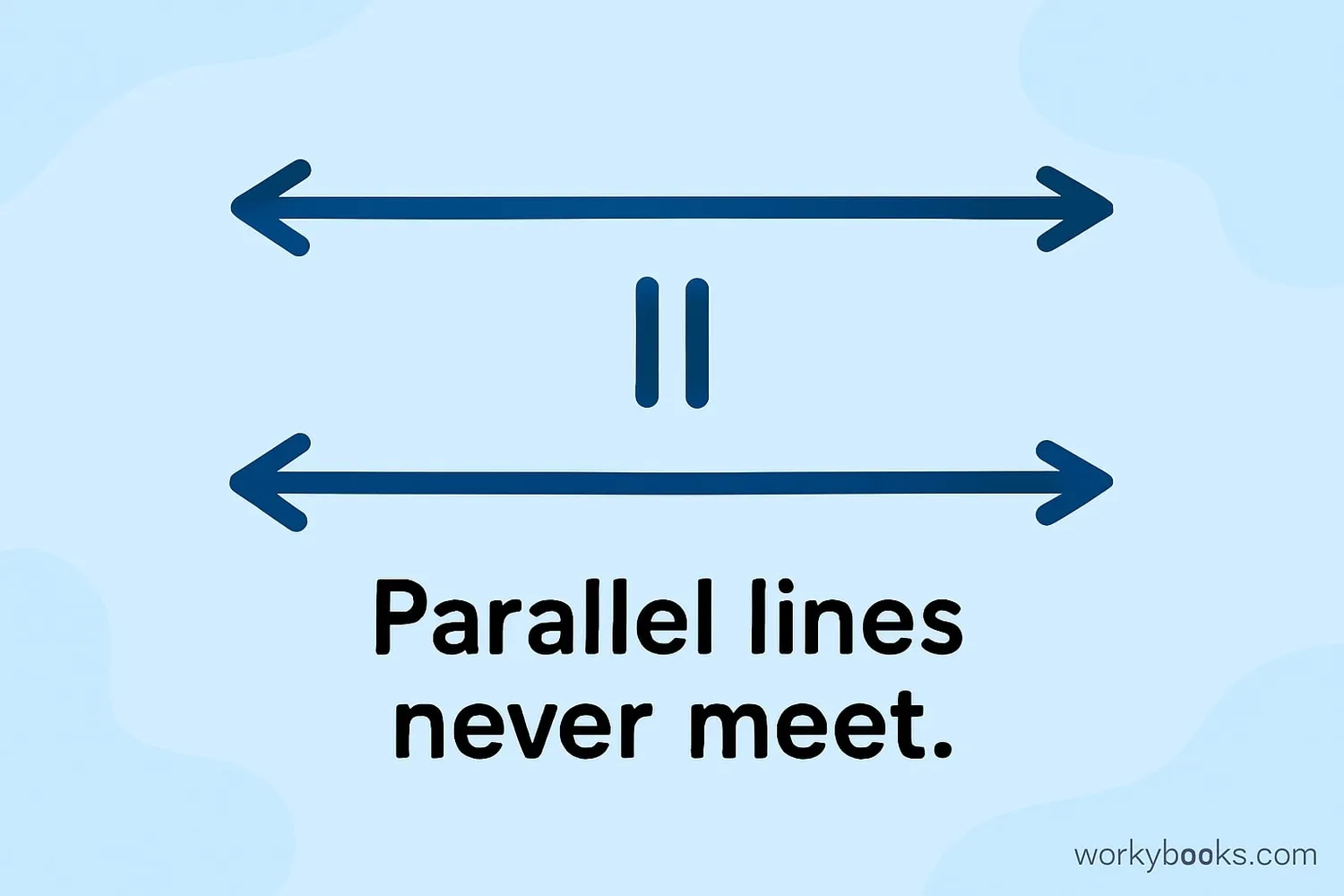
Parallel lines are lines in a plane that never meet. They are always the same distance apart, no matter how far you extend them in either direction.
Think of railroad tracks - they run side by side but never cross. In geometry, we use a special symbol to show that lines are parallel: ||. For example, if line AB is parallel to line CD, we write: AB || CD.
Parallel lines are important in geometry because they create special relationships when crossed by another line (called a transversal). These relationships help us solve many geometric problems.
Key Concept
Parallel lines are always the same distance apart and never intersect, no matter how far they are extended.
Properties of Parallel Lines
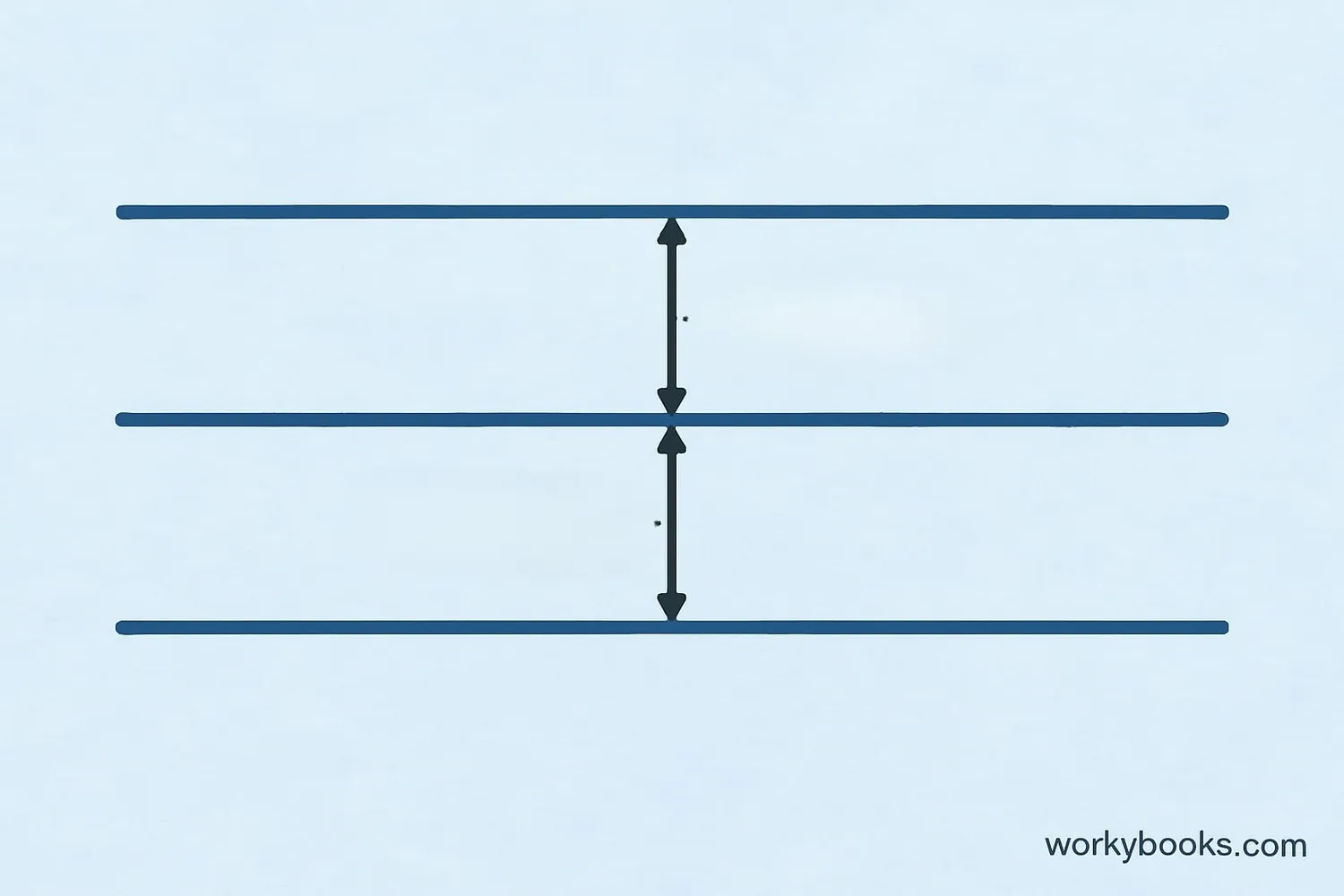
Parallel lines have several important properties:
Equidistant Property
The distance between two parallel lines remains constant everywhere. This is why they never meet.
Never Intersect
No matter how far you extend parallel lines in either direction, they will never cross each other.
Transitive Property
If line A is parallel to line B, and line B is parallel to line C, then line A is parallel to line C.
Slope Equality
In coordinate geometry, parallel lines have identical slopes. This is how we identify them on graphs.
Remember
Parallel lines must be straight and in the same plane. Curved lines that never meet are not considered parallel in geometry.
Parallel Lines with a Transversal
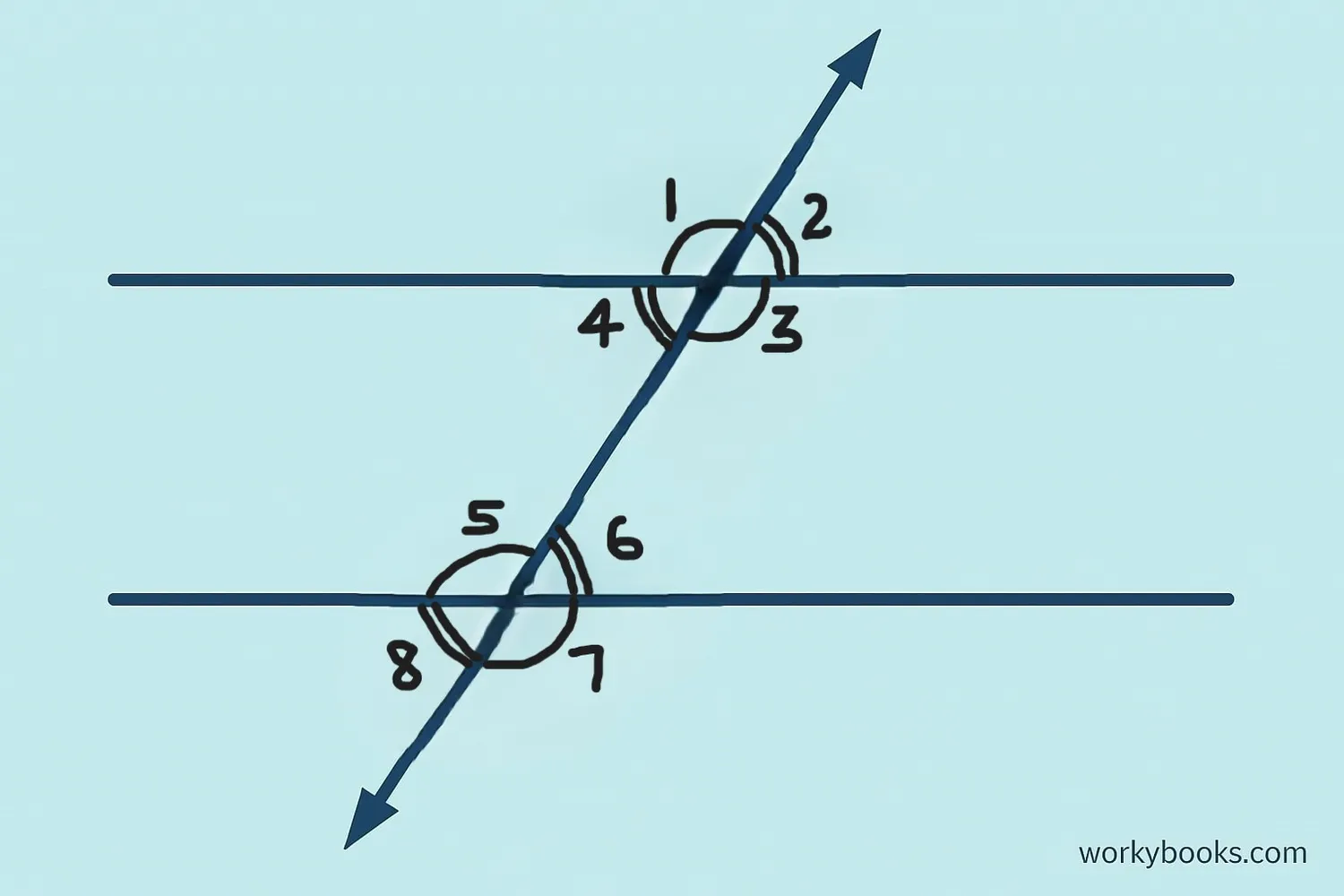
When a transversal (a line that crosses two or more other lines) intersects two parallel lines, it creates special angle relationships:
Angle Relationships
Corresponding angles are in matching positions on the same side of the transversal. For example, angles in the top-left position above each parallel line.
Alternate interior angles are on opposite sides of the transversal and between the parallel lines.
Alternate exterior angles are on opposite sides of the transversal and outside the parallel lines.
Consecutive interior angles (also called co-interior angles) are on the same side of the transversal and between the parallel lines. These angles add up to 180°.
Quick Tip
When you see parallel lines crossed by a transversal, look for the "F" pattern for corresponding angles and the "Z" pattern for alternate angles.
Slope of Parallel Lines
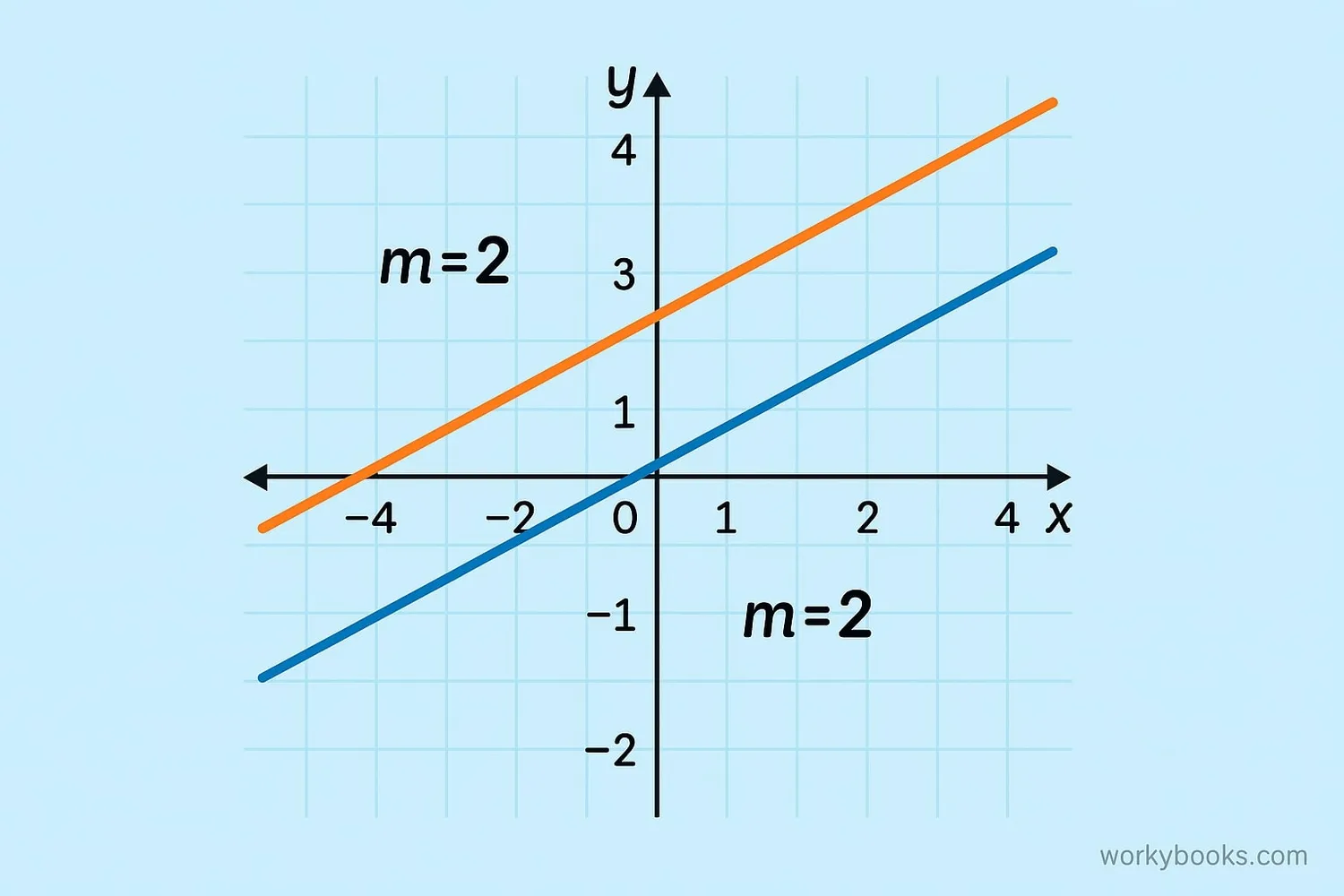
In coordinate geometry, we can identify parallel lines by their slopes. The slope of a line measures its steepness and is usually represented by the letter "m".
Key Rule: Two non-vertical lines are parallel if and only if they have the same slope.
For example, if line A has a slope of 3, and line B also has a slope of 3, then they are parallel. If line C has a slope of -1/2, then any line with a slope of -1/2 will be parallel to line C.
Vertical lines are a special case. All vertical lines are parallel to each other because they all have undefined slope.
Parallel Line Equations
Two lines with the same slope (m) but different y-intercepts (b) are parallel.
Remember
Horizontal lines (slope = 0) are also parallel to each other. For example, y = 3 and y = -2 are parallel horizontal lines.
Real World Examples

Parallel lines are all around us in everyday life. Here are some common examples:
Railroad Tracks: The most classic example - the rails are always parallel to each other.
Notebook Paper: The horizontal lines on ruled paper are parallel to each other.
Building Structures: The opposite sides of doors, windows, and buildings are often parallel.
Road Markings: The lines separating lanes on a highway are parallel.
Bookshelves: The shelves are parallel to each other and to the floor/ceiling.
Sports Fields: The lines on soccer fields, basketball courts, and running tracks are parallel.
Observation Tip
Look for pairs of straight lines that remain the same distance apart to identify parallel lines in the real world.
Parallel Lines Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about parallel lines:
Geometry Trivia
Discover interesting facts about parallel lines and geometry:
Euclid's Fifth Postulate
The concept of parallel lines is based on Euclid's Fifth Postulate, which mathematicians tried to prove for over 2000 years before realizing it was independent of the other postulates.
Parallel Universes
In physics, the concept of parallel lines inspired the idea of parallel universes - separate universes that exist alongside our own but never intersect.
Art Perspective
In art, parallel lines appear to converge at a vanishing point to create the illusion of depth. This technique is called linear perspective.
Railroad Engineering
Railroad engineers must maintain exact parallelism between tracks. Even a 1-inch deviation over 10 miles could cause trains to derail at high speeds.





