Partial Product - Definition, Examples, Quiz, FAQ, Trivia
Understanding Multiplication Using the Partial Products Method
What is Partial Product?
Partial product is a multiplication strategy that helps us multiply larger numbers by breaking them into smaller, easier parts. Think of it like solving a puzzle by putting together smaller pieces!
When we use the partial products method, we multiply each digit of one number by each digit of the other number separately, then add all the results together. This makes multiplication easier because we're working with smaller numbers.
Math Tip!
Partial products help you understand what multiplication really means - it's like repeated addition but organized in a special way that makes large numbers easier to work with.
How Partial Product Multiplication Works
The partial products method works by expanding numbers into their place values and multiplying each part separately. Here's how it works:
Expand Numbers
Break each number into its place values (tens, ones, etc.)
Multiply Parts
Multiply each part of one number by each part of the other
List Products
Write down all the smaller multiplication results
Add Together
Add all the partial products to get the final answer
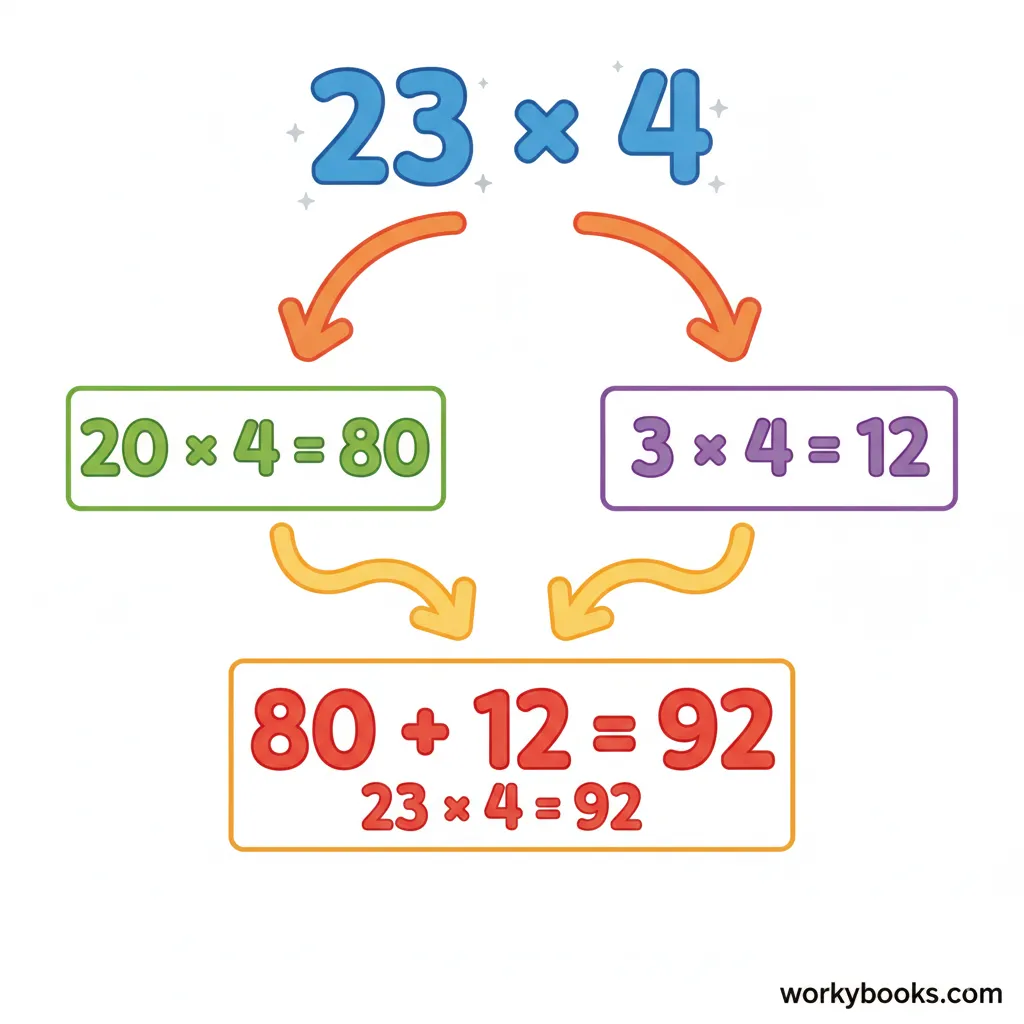
Let's look at a simple example: 23 × 4
First, we break 23 into 20 + 3
Then we multiply: 20 × 4 = 80 and 3 × 4 = 12
Finally, we add: 80 + 12 = 92
So, 23 × 4 = 92
Partial Product Examples
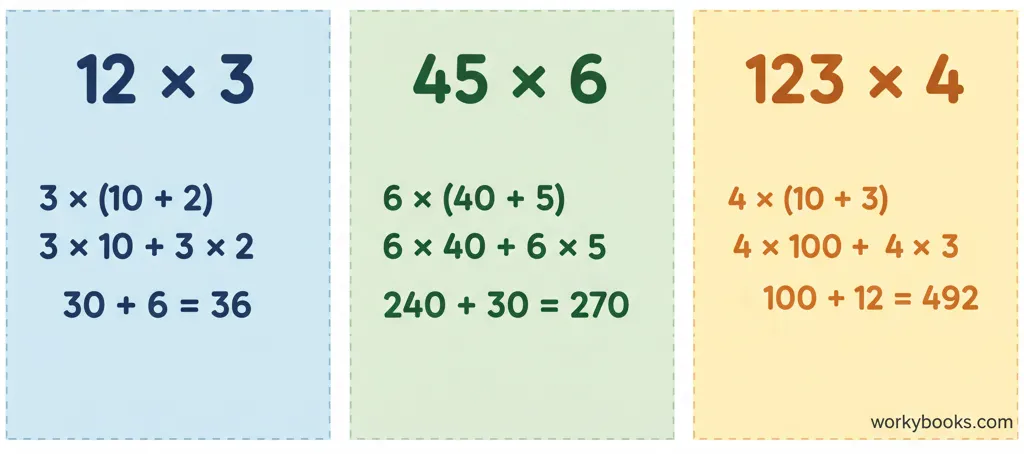
Let's look at some examples to see how partial products work with different numbers:
14 = 10 + 4
10 × 3 = 30
4 × 3 = 12
30 + 12 = 42
So, 14 × 3 = 42
25 = 20 + 5
20 × 4 = 80
5 × 4 = 20
80 + 20 = 100
So, 25 × 4 = 100
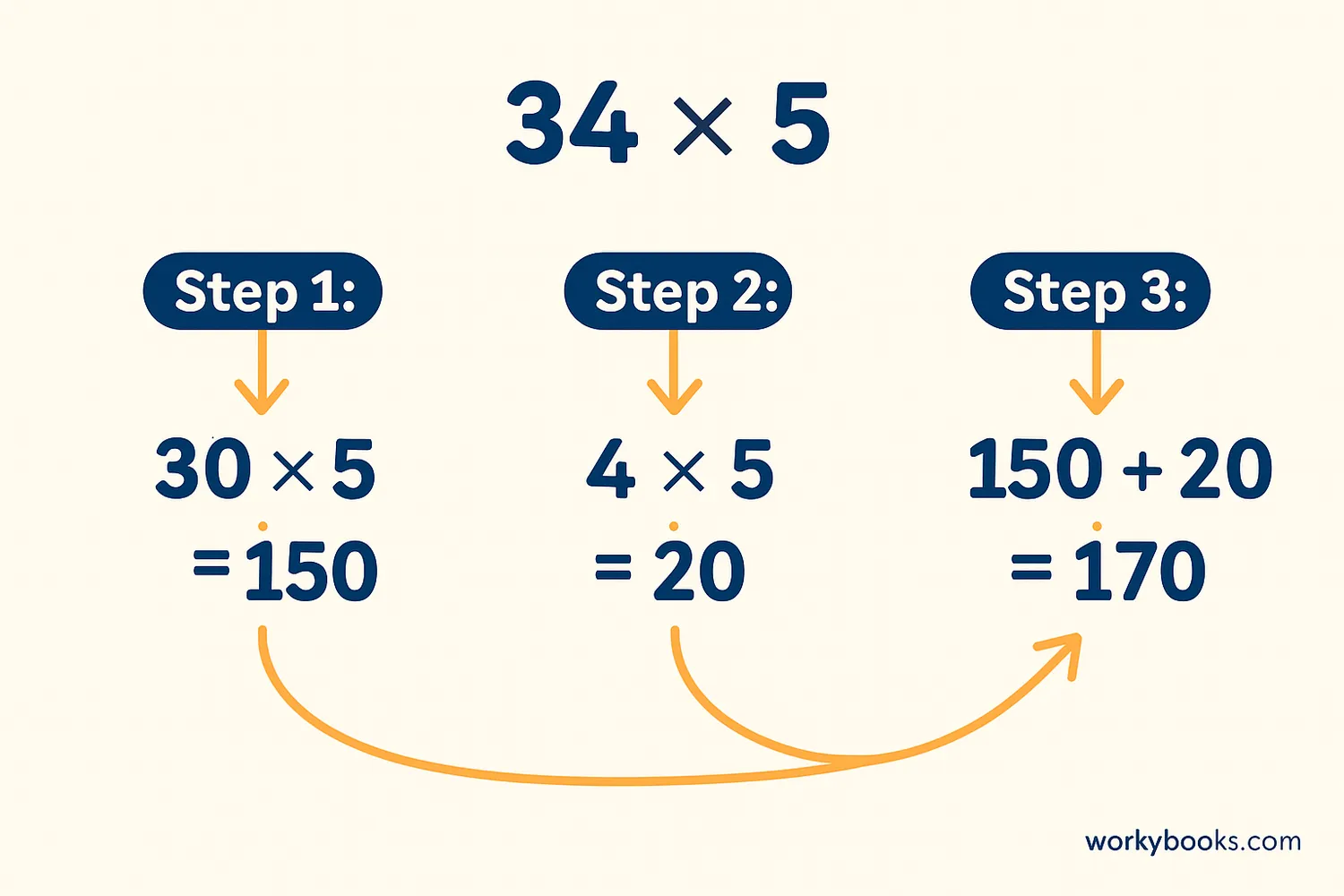
36 = 30 + 6
30 × 5 = 150
6 × 5 = 30
150 + 30 = 180
So, 36 × 5 = 180
For larger numbers, we can break both numbers into their place values. Let's try 23 × 12:
23 = 20 + 3
12 = 10 + 2
20 × 10 = 200
20 × 2 = 40
3 × 10 = 30
3 × 2 = 6
200 + 40 + 30 + 6 = 276
So, 23 × 12 = 276
Did You Know?
The partial products method helps build a strong foundation for understanding the standard multiplication algorithm you'll learn later. It shows you exactly what happens when you multiply numbers.
Partial Product Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about partial products.
Frequently Asked Questions
Here are answers to some common questions about partial products:
Math Facts About Partial Products
Discover some fascinating facts about multiplication and partial products!
Historical Methods
Ancient civilizations like the Egyptians used a doubling method similar to partial products. They would repeatedly double numbers to solve multiplication problems!
Place Value Power
The partial products method shows why place value is so important in math. Understanding that 34 means 30 + 4 helps make multiplication much easier.
Mental Math Helper
Once you're comfortable with partial products, you can use them for quick mental math. For example, 16×4 is easier to calculate as 10×4=40 plus 6×4=24 equals 64.
Algebra Connection
Partial products use the same idea as the distributive property in algebra: a×(b+c) = a×b + a×c. You're learning algebra concepts when you use partial products!





