Partition - Definition, Examples, Quiz, FAQ, Trivia
Understanding How to Break Numbers and Shapes Into Equal Parts
What is Partitioning?
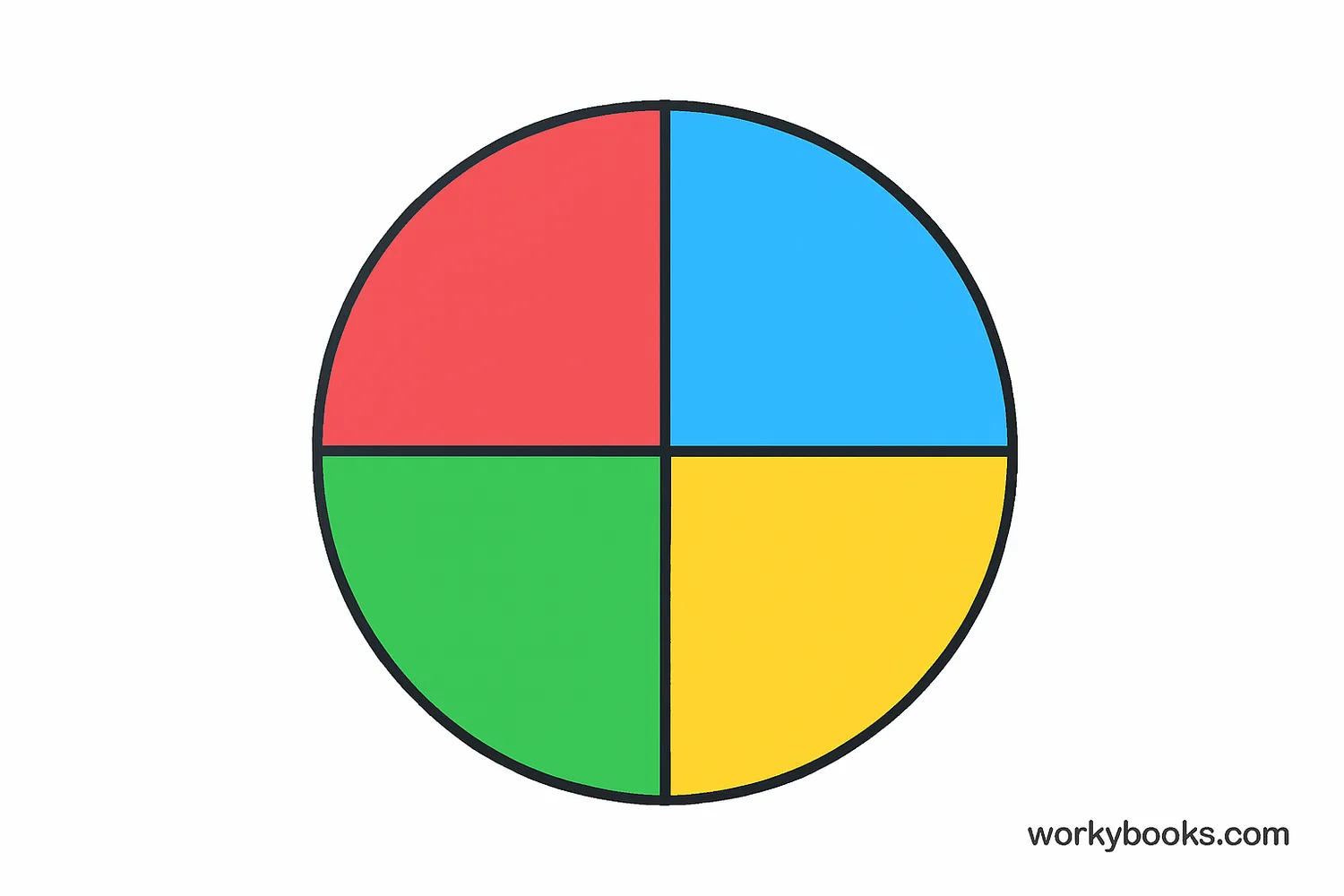
Partitioning is a math word that means breaking something into smaller parts. Think of it like sharing a pizza with friends - you cut it into slices so everyone gets an equal piece!
When we partition in math, we're dividing numbers or shapes into equal groups or parts. This helps us understand how numbers work and how to share things fairly.
Math Fact!
Partitioning helps build a strong foundation for understanding more complex math concepts like fractions, division, and multiplication.
Partitioning Numbers
Partitioning numbers means breaking them into smaller numbers that add up to the original number. For example, the number 10 can be partitioned in many different ways:
10 = 5 + 5
Two equal parts
10 = 7 + 3
Two different parts
10 = 4 + 3 + 3
Three parts
10 = 2 + 2 + 2 + 2 + 2
Five equal parts
Partitioning helps us understand that numbers are made up of other numbers. This is really helpful when we learn to add and subtract!
Example: Partitioning 8
We can partition 8 in many ways: 5+3, 4+4, 6+2, 7+1, or even 2+2+2+2. All these combinations add up to 8!
Partitioning in Fractions
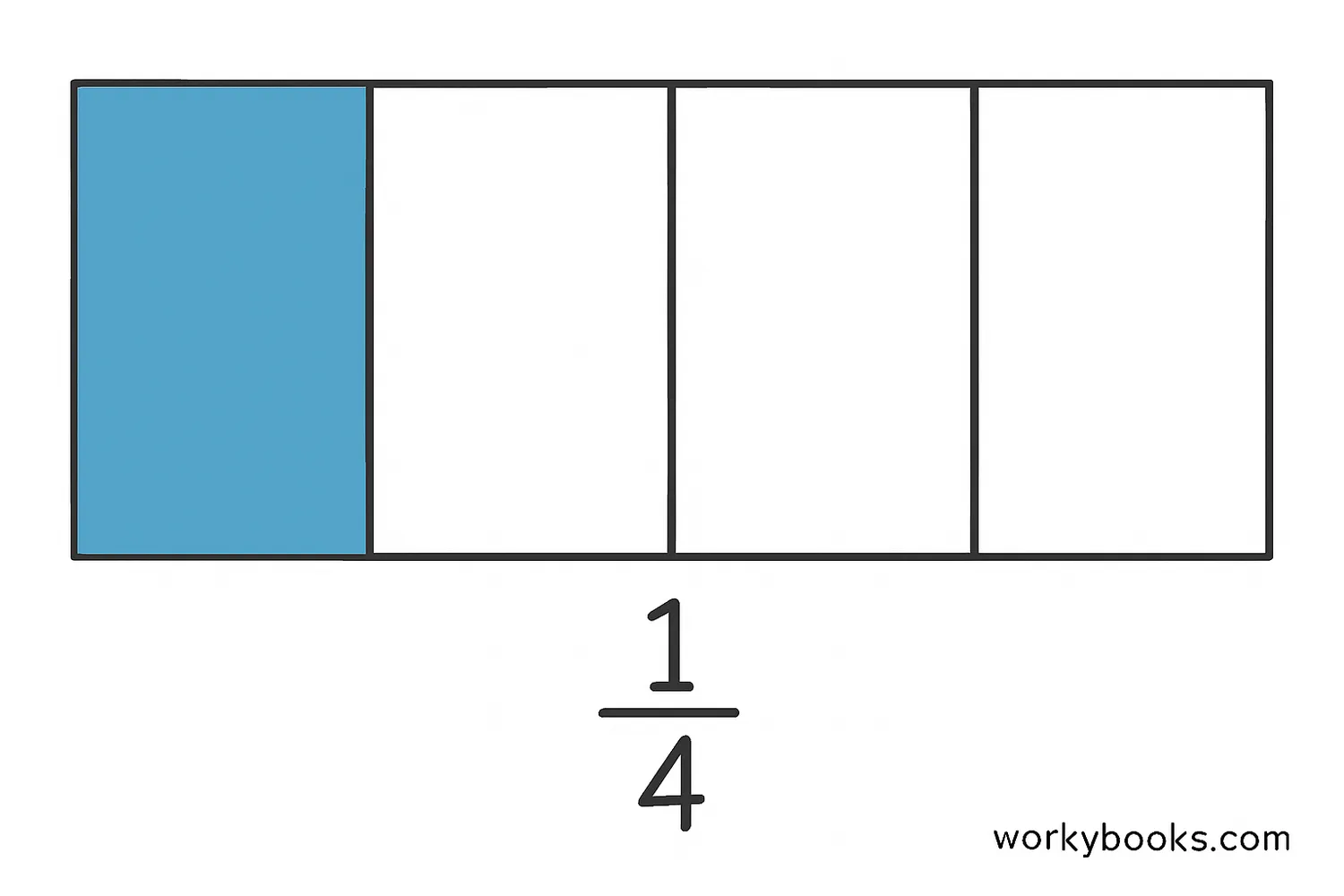
Fractions are all about partitioning! When we write a fraction like 1/2, it means we've partitioned a whole into 2 equal parts and we're talking about 1 of those parts.
Equal Parts
For fractions to work correctly, all parts must be equal in size
Denominator
The bottom number tells us how many equal parts we partitioned the whole into
Numerator
The top number tells us how many of those parts we're talking about
When we partition shapes into equal parts, we're creating fractions. The more parts we create, the smaller each part becomes.
Example: Partitioning a Circle
If we partition a circle into 4 equal parts, each part is 1/4 of the whole circle. If we partition it into 8 equal parts, each part is 1/8 of the whole circle.
Examples of Partitioning

Partitioning happens all around us in everyday life. Here are some common examples:
Sharing Food
Cutting a pizza or cake into slices so everyone gets an equal piece
Time Management
Dividing your day into hours for different activities
Money
Breaking a dollar into quarters, dimes, nickels, and pennies
Measuring
Dividing a ruler into inches or centimeters
Games
Dividing players into teams with equal numbers
Partitioning helps us solve problems by breaking them into smaller, more manageable parts. This is an important thinking skill in math and in life!
Did You Know?
The word "partition" comes from the Latin word "partitio," which means "division" or "sharing."
Partitioning Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about partitioning.
Frequently Asked Questions
Here are answers to some common questions about partitioning:
Math Facts About Partitioning
Discover some fascinating facts about partitioning and numbers!
Many Ways to Partition
The number 10 can be partitioned in 42 different ways if we consider the order of parts! That's why understanding partitioning helps with addition facts.
Ancient Concept
Partitioning has been used since ancient times. The Egyptians used partitioning in their fraction system over 4,000 years ago!
Pattern Discovery
Mathematicians have discovered patterns in how numbers can be partitioned. For example, the number of ways to partition a number grows very quickly as the number gets larger.
Real-World Applications
Partitioning is used in computer science for dividing tasks among processors, in economics for resource allocation, and in cooking for recipe measurements!





