Place Value - Definition, Examples, Quiz, FAQ, Trivia
Learn how digits get their value based on their position in a number with clear explanations and practice activities
What is Place Value?

Place value is the value of each digit in a number based on its position. In our number system, each position represents a power of 10. This means the same digit can have different values depending on where it's placed in the number.
For example, in the number 555:
- The first 5 is in the hundreds place and represents 500
- The second 5 is in the tens place and represents 50
- The third 5 is in the ones place and represents 5
Our number system is called a base-10 system because each place is 10 times the value of the place to its right. This makes it easy to work with large numbers by following consistent patterns.
Key Concept
The position of a digit determines its value. Moving left, each place is 10 times greater. Moving right, each place is 10 times smaller.
Place Value Chart
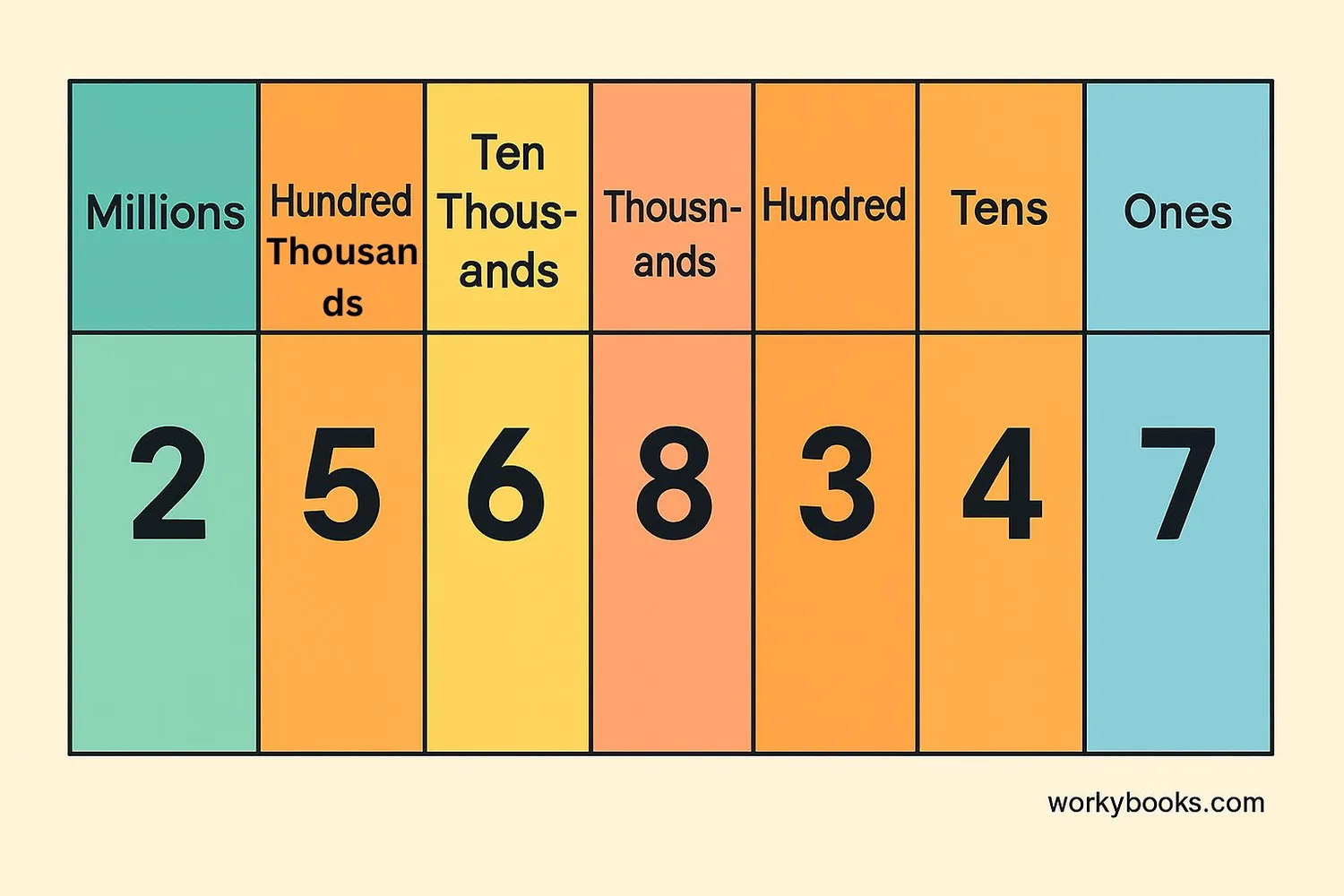
A place value chart helps visualize how our number system works. Here's how the places stack up:
The number shown above is 1,234,567. Notice how:
- The 7 is worth exactly 7 (ones place)
- The 6 is worth 60 (6 × 10)
- The 5 is worth 500 (5 × 100)
- The 4 is worth 4,000 (4 × 1,000)
- And so on, with each place being 10 times the previous
Remember
Each move to the left in the place value chart multiplies the digit's value by 10. Each move to the right divides by 10.
Face Value vs Place Value

It's important to understand the difference between face value and place value:
Face Value: The actual value of the digit itself, regardless of its position in the number.
Place Value: The value of the digit based on its position in the number.
Let's look at the number 3,762:
- The digit 3 has a face value of 3 and a place value of 3,000
- The digit 7 has a face value of 7 and a place value of 700
- The digit 6 has a face value of 6 and a place value of 60
- The digit 2 has a face value of 2 and a place value of 2
Face value never changes, but place value depends entirely on the digit's position!
Key Difference
Face value is the digit itself. Place value is the digit multiplied by its place (ones, tens, hundreds, etc.).
Decimals Place Value

Place value continues after the decimal point, with each place being 10 times smaller than the previous:
For the number 25.836:
- The 2 is in the tens place (20)
- The 5 is in the ones place (5)
- The 8 is in the tenths place (0.8 or 8/10)
- The 3 is in the hundredths place (0.03 or 3/100)
- The 6 is in the thousandths place (0.006 or 6/1000)
The decimal point separates the whole number part from the fractional part. Just like with whole numbers, each move to the right divides the value by 10.
Decimal Tip
Remember that the first place after the decimal is tenths (1/10), then hundredths (1/100), then thousandths (1/1000), and so on.
Expanded Form

Expanded form is a way to write numbers that shows the value of each digit. It breaks the number into the sum of each digit multiplied by its place value.
Example with 7,351:
For decimal numbers, we continue the pattern after the decimal point:
Example with 24.608:
Expanded form helps us understand exactly how much each digit contributes to the total value of the number.
Practice Tip
Try writing numbers in expanded form to strengthen your understanding of place value. Start with 3-digit numbers, then try larger numbers and decimals.
Place Value Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about place value:
Number System Trivia
Discover interesting facts about numbers and place value:
Origin of Place Value
The place value system we use today was developed in India around the 5th century and later spread to the Middle East and Europe. Before this, number systems like Roman numerals didn't have place value, making calculations much harder.
Importance of Zero
The concept of zero as a placeholder was crucial for developing place value. Ancient Babylonian and Mayan civilizations had place value systems but struggled without a proper zero. The Indian mathematician Brahmagupta formalized zero's role in the 7th century.
Naming Large Numbers
Our place value system continues infinitely in both directions. After millions come billions, trillions, quadrillions, etc. The names follow Latin prefixes, with each new term representing 1,000 times the previous (every three place values).
Computers Use Place Value
Computers use binary (base-2) place value where each digit is either 0 or 1. Each position represents a power of 2. For example, 101 in binary is 1×4 + 0×2 + 1×1 = 5 in decimal. This shows place value works the same in any base.





