Polynomials - Definition, Examples, Quiz, FAQ, Trivia
Learn about polynomial expressions with simple explanations, examples, and practice activities
What Are Polynomials?
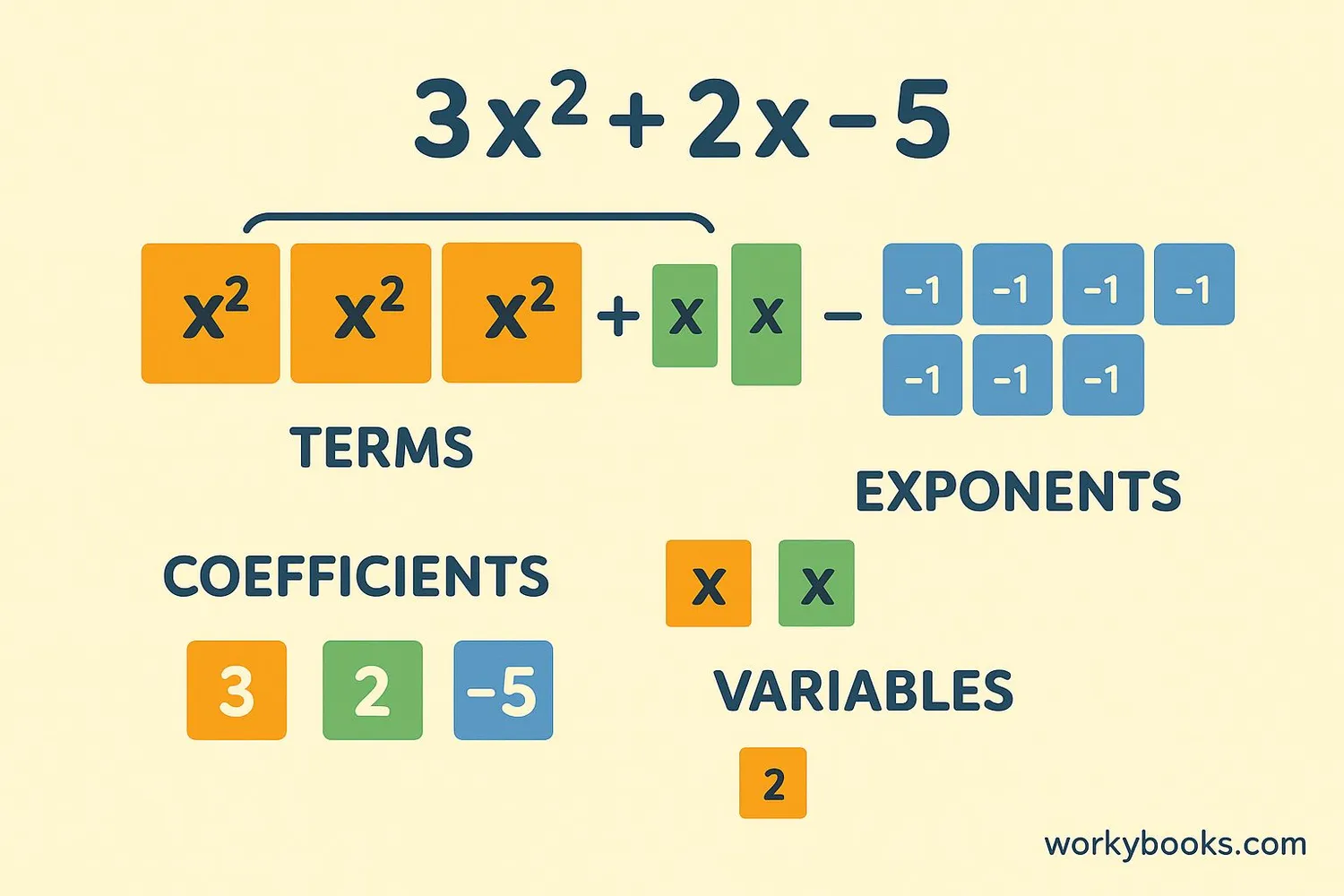
A polynomial is a special kind of math expression made up of terms added together. Each term has:
• A coefficient (the number in front)
• A variable (like x or y)
• An exponent (the little number that shows how many times to multiply the variable)
For example: 3x² + 2x - 5 is a polynomial with three terms.
Polynomials are like math sentences that help us describe patterns, solve problems, and model real-world situations. They can be simple (like x + 2) or complex (like 4x³ - 2x² + 7x - 1).
General Polynomial Form
Where a's are coefficients, x is the variable, and n is the degree (highest exponent).
Key Concept
Polynomials cannot have:
• Variables in denominators (like 1/x)
• Negative exponents (like x⁻²)
• Fractional exponents (like x½)
Types of Polynomials
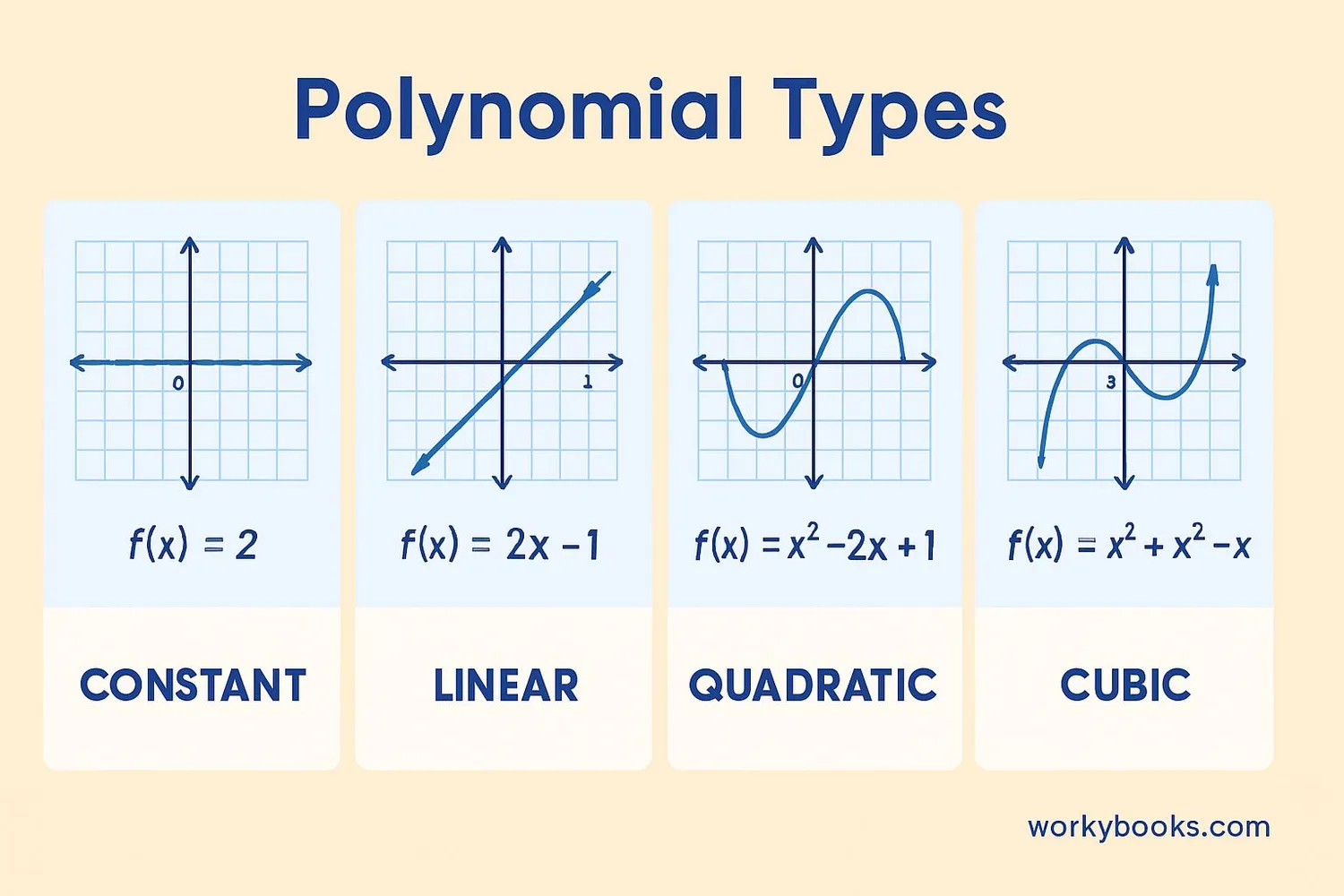
Polynomials are classified by their degree - the highest exponent in the expression:
| Degree | Name | Example | Shape |
|---|---|---|---|
| 0 | Constant | 5 | Horizontal line |
| 1 | Linear | 2x + 3 | Straight line |
| 2 | Quadratic | x² - 4x + 4 | Parabola (U-shape) |
| 3 | Cubic | x³ - 2x² | S-shaped curve |
| 4 | Quartic | x⁴ - 3x² + 1 | W-shaped |
Polynomials can also be classified by the number of terms:
• Monomial: 1 term (like 3x²)
• Binomial: 2 terms (like x + 5)
• Trinomial: 3 terms (like 2x² - x + 7)
Remember
The degree tells us about the polynomial's behavior and how many solutions (roots) it might have.
Polynomial Operations

We can perform different operations with polynomials:
Adding Polynomials
Combine like terms (terms with the same variable and exponent):
Example: (3x² + 2x - 5) + (4x² - x + 3)
= (3x² + 4x²) + (2x - x) + (-5 + 3)
= 7x² + x - 2
Multiplying Polynomials
Use the distributive property (FOIL method for binomials):
Example: (x + 2)(x + 3)
= x·x + x·3 + 2·x + 2·3
= x² + 3x + 2x + 6
= x² + 5x + 6
Operation Tip
When multiplying, add exponents: x² × x³ = x⁵ (2 + 3 = 5)
Real-World Examples

Polynomials are used in many real-world situations:
Example 1: Area calculations
A rectangular garden has length (x + 3) meters and width (x + 2) meters.
Area = length × width = (x + 3)(x + 2) = x² + 5x + 6 square meters
Example 2: Projectile motion
The height h of a ball thrown upward can be modeled by:
h = -16t² + 32t + 5 (where t is time in seconds)
Example 3: Business profits
A company's profit P might be P = -2x² + 100x - 800
where x is the number of items sold
Example 4: Geometry problems
The volume of a box with sides (x), (x + 1), and (x + 2) is:
V = x(x + 1)(x + 2) = x³ + 3x² + 2x
Application Tip
Quadratic polynomials often appear in problems involving area, motion, and optimization.
Polynomial Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about polynomials:
Math Trivia
Discover interesting facts about polynomials and math history:
Ancient Polynomials
The Babylonians were solving quadratic equations as early as 2000 BCE! They used geometric methods since they didn't have modern algebraic notation.
Polynomials in Nature
Many natural patterns can be modeled with polynomials. The path of a thrown ball, the growth of plants, and even sound waves can be described using polynomial equations.
Space Calculations
NASA uses high-degree polynomials to calculate rocket trajectories. The curves need to be very precise to get spacecraft to their destinations!
Polynomial Records
The longest polynomial ever factored had 1,200 terms! Mathematicians used supercomputers to break it down into simpler parts.




