Proportions - Definition, Examples, Quiz, FAQ, Trivia
Learn about ratios, direct and inverse proportions with easy explanations and practice activities
What is Proportion?

A proportion shows that two ratios are equal. Think of it like a balance scale where both sides have the same weight. In math, we write proportions like this:
Proportion Formula
This means the ratio of a to b is equal to the ratio of c to d
When two ratios are equal, they form a proportion. This tells us that the relationship between the quantities is the same. Proportions help us solve many real-world problems!
Key Concept
Proportion means two ratios are equal. If a/b = c/d, then a, b, c, d are in proportion.
Types of Proportion
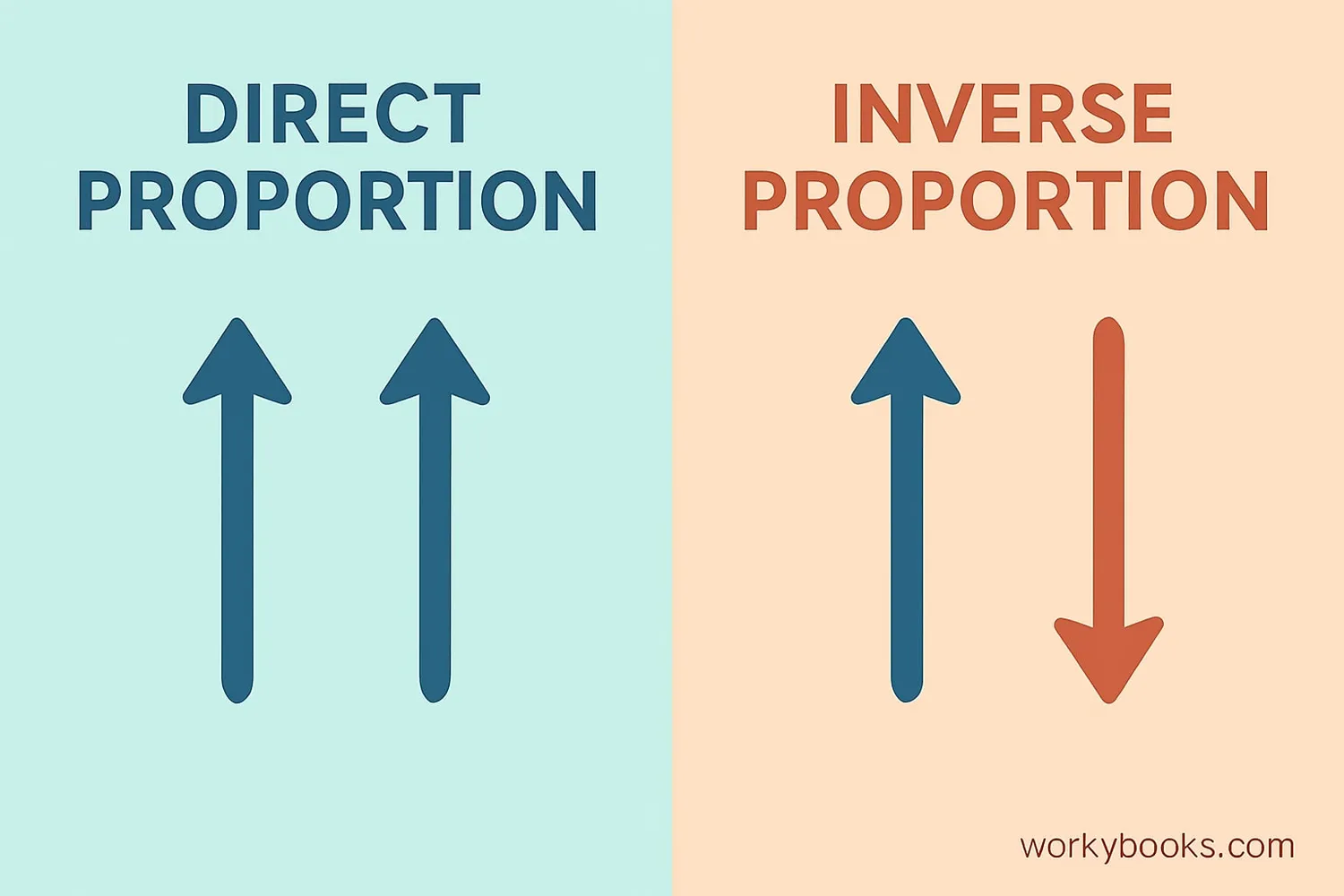
There are two main types of proportion: direct and inverse. Understanding these helps us solve different kinds of problems.
Direct Proportion
When one quantity increases, the other also increases at the same rate.
Example: More people = more food needed
Inverse Proportion
When one quantity increases, the other decreases at the same rate.
Example: More workers = less time needed
Direct Proportion
In direct proportion, if one quantity doubles, the other also doubles. If one halves, the other halves too. They change together in the same way.
Example: The cost of apples. If 1 apple costs $1, then 2 apples cost $2, 3 apples cost $3, and so on. The cost is directly proportional to the number of apples.
Inverse Proportion
In inverse proportion, if one quantity doubles, the other halves. They change in opposite ways.
Example: Speed and time. If you travel at 60 km/h, it takes 1 hour to go 60 km. If you travel at 120 km/h (twice as fast), it takes only 30 minutes (half the time) to go the same distance.
Remember
Direct proportion: Both increase or both decrease together. Inverse proportion: One increases while the other decreases.
How to Calculate Proportion
Solving proportion problems is like solving a puzzle! Follow these steps:
Example Problem
If 3 pencils cost 60 cents, how much do 5 pencils cost?
- Set up two equal ratios: pencils/cost = pencils/cost → 3/60 = 5/x
- Cross-multiply: 3 × x = 60 × 5 → 3x = 300
- Solve for x: x = 300 ÷ 3 = 100
So 5 pencils cost 100 cents (or $1.00)!
Cross-Multiplication Method
This is the most reliable way to solve proportions:
For a proportion a/b = c/d, we can cross-multiply: a × d = b × c
Calculation Tip
Always make sure your ratios compare the same things in the same order (like pencils to cost in both ratios).
Proportion Examples

Proportions are everywhere in our daily lives! Here are some common examples:
Example 1: Cooking (Direct Proportion)
A cookie recipe needs 2 cups of flour for 24 cookies. How much flour for 36 cookies?
Set up proportion: 2/24 = x/36
Cross-multiply: 2 × 36 = 24 × x → 72 = 24x
Solve: x = 72 ÷ 24 = 3 cups of flour
Example 2: Map Scales (Direct Proportion)
A map scale shows 1 cm = 5 km. How many km is 4 cm on the map?
Proportion: 1/5 = 4/x
Cross-multiply: 1 × x = 5 × 4 → x = 20 km
Example 3: Work Problems (Inverse Proportion)
4 workers can build a fence in 6 hours. How long would it take 8 workers?
Since more workers means less time, this is inverse proportion.
Set up: 4 workers × 6 hours = 8 workers × x hours
Solve: 24 = 8x → x = 24 ÷ 8 = 3 hours
Real-World Tip
Look for proportions in recipes, maps, speed limits, shopping discounts, and many other everyday situations!
Proportion Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about proportions:
Math Trivia
Discover interesting facts about proportions and mathematics:
Ancient Proportions
The concept of proportion dates back to ancient Egypt and Babylon. The Egyptians used proportions in building pyramids, ensuring their structures were mathematically precise.
Golden Ratio
The Golden Ratio (about 1.618:1) is a special proportion found in nature and art. It appears in seashells, flowers, and famous artworks like the Mona Lisa.
Proportional Scales
Proportions help scientists create scale models. A model airplane might be 1:100 scale, meaning 1 cm on the model equals 100 cm (1 meter) on the real airplane.
Body Proportions
Your arm span (fingertip to fingertip) is usually proportional to your height! For most people, these measurements are almost equal.





