Quadrants - Definition, Examples, Quiz, FAQ, Trivia
Learn about the four sections of the coordinate plane with simple explanations and activities
What is a Quadrant?
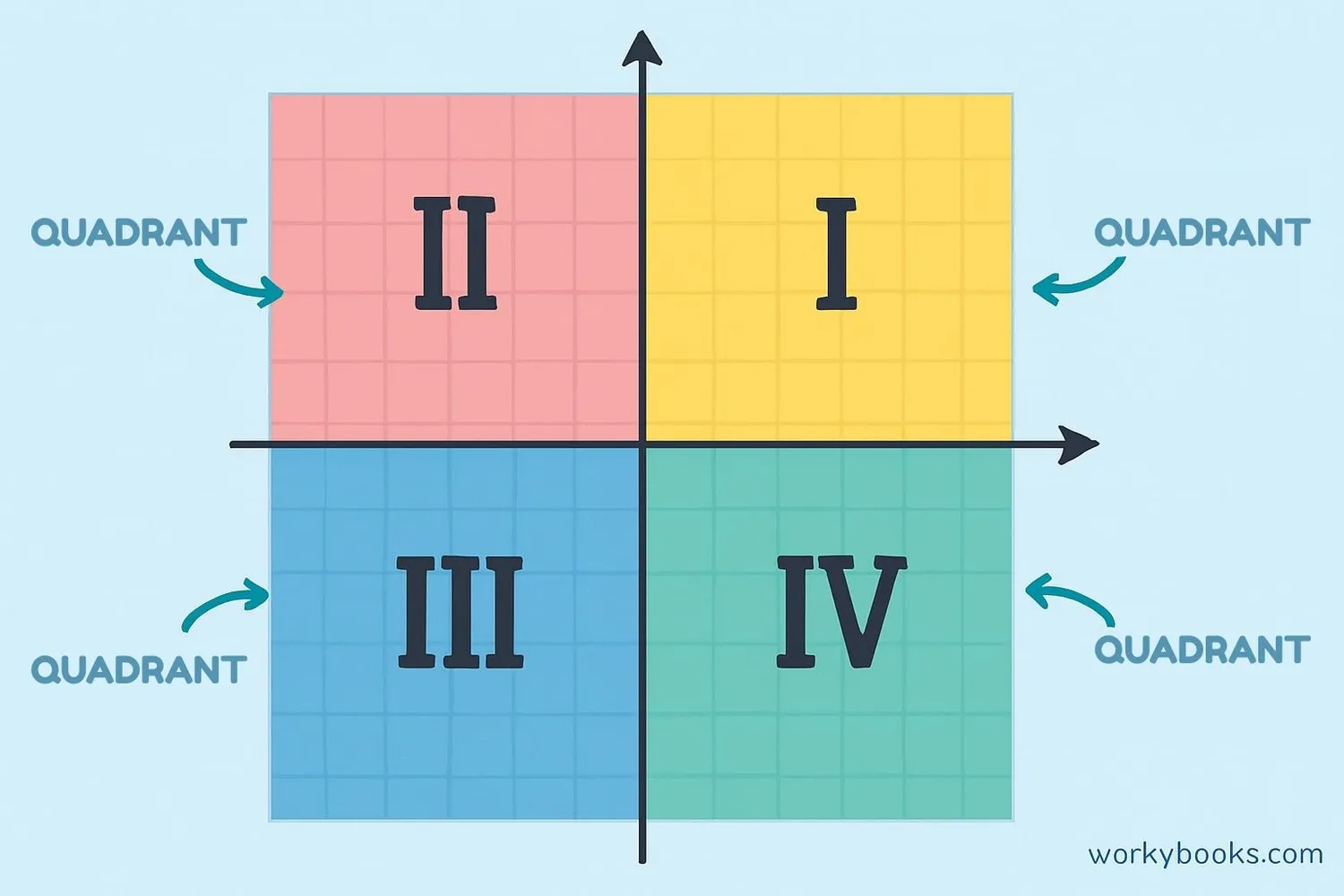
A quadrant is one of the four sections that make up the coordinate plane. Think of the coordinate plane like a big plus sign. The horizontal line is called the x-axis and the vertical line is called the y-axis. These two lines cross at a special point called the origin (0,0).
The axes divide the plane into four regions called quadrants. We label them with Roman numerals:
- Quadrant I (top-right)
- Quadrant II (top-left)
- Quadrant III (bottom-left)
- Quadrant IV (bottom-right)
Key Concept
Quadrants help us describe where points are located on the coordinate plane. Each quadrant has its own special characteristics.
The Coordinate Plane and Quadrants
The coordinate plane (also called the Cartesian plane) is like a map for mathematics. It has two number lines that cross at the origin (0,0):
X-axis: The horizontal number line (left to right)
Y-axis: The vertical number line (up and down)
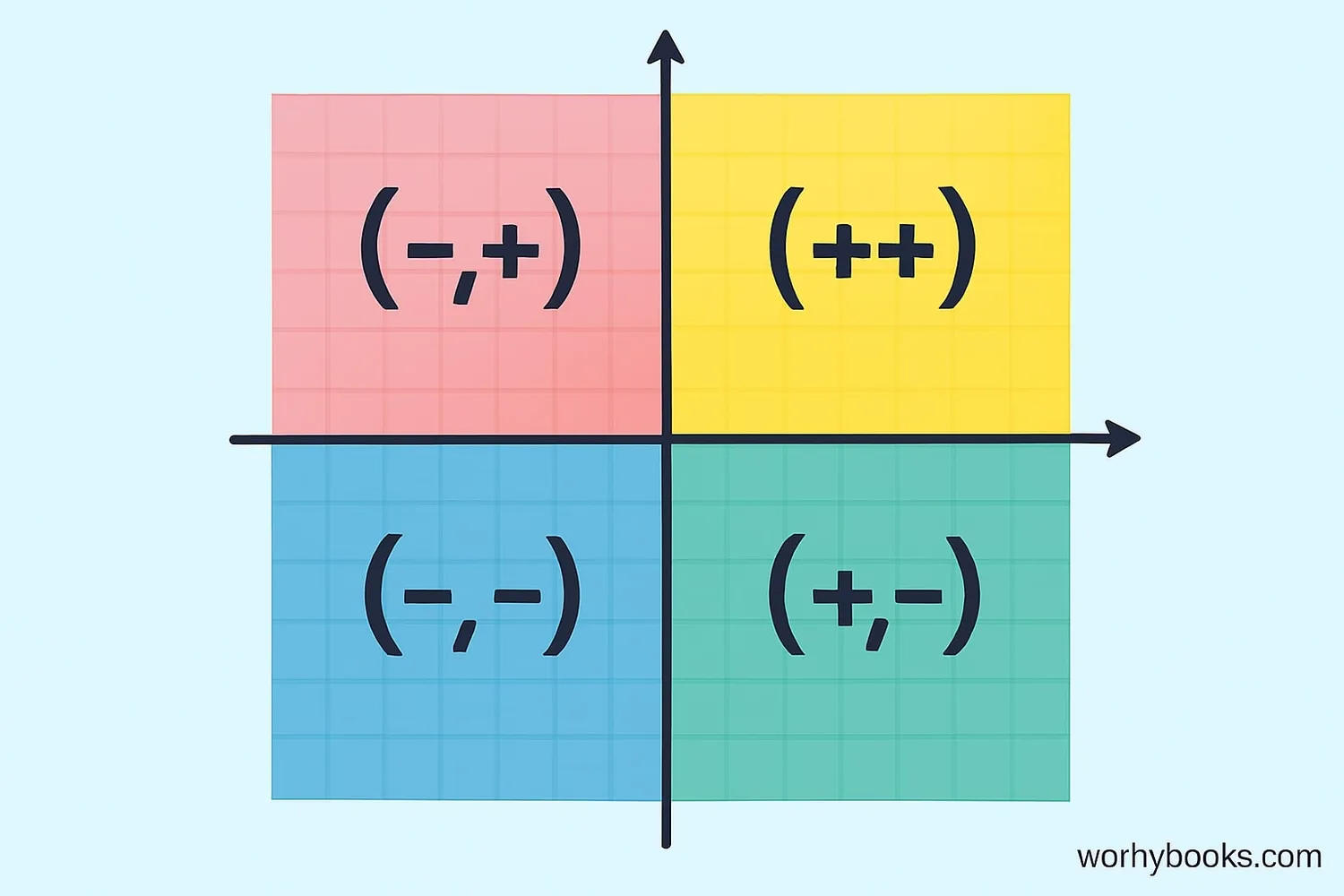
Each quadrant has special properties:
Quadrant I
Both x and y coordinates are positive (+x, +y)
Quadrant II
X is negative, y is positive (-x, +y)
Quadrant III
Both x and y coordinates are negative (-x, -y)
Quadrant IV
X is positive, y is negative (+x, -y)
Remember
Quadrants are numbered counterclockwise starting from the top right. Always start with Quadrant I when numbering.
Plotting Points in Quadrants
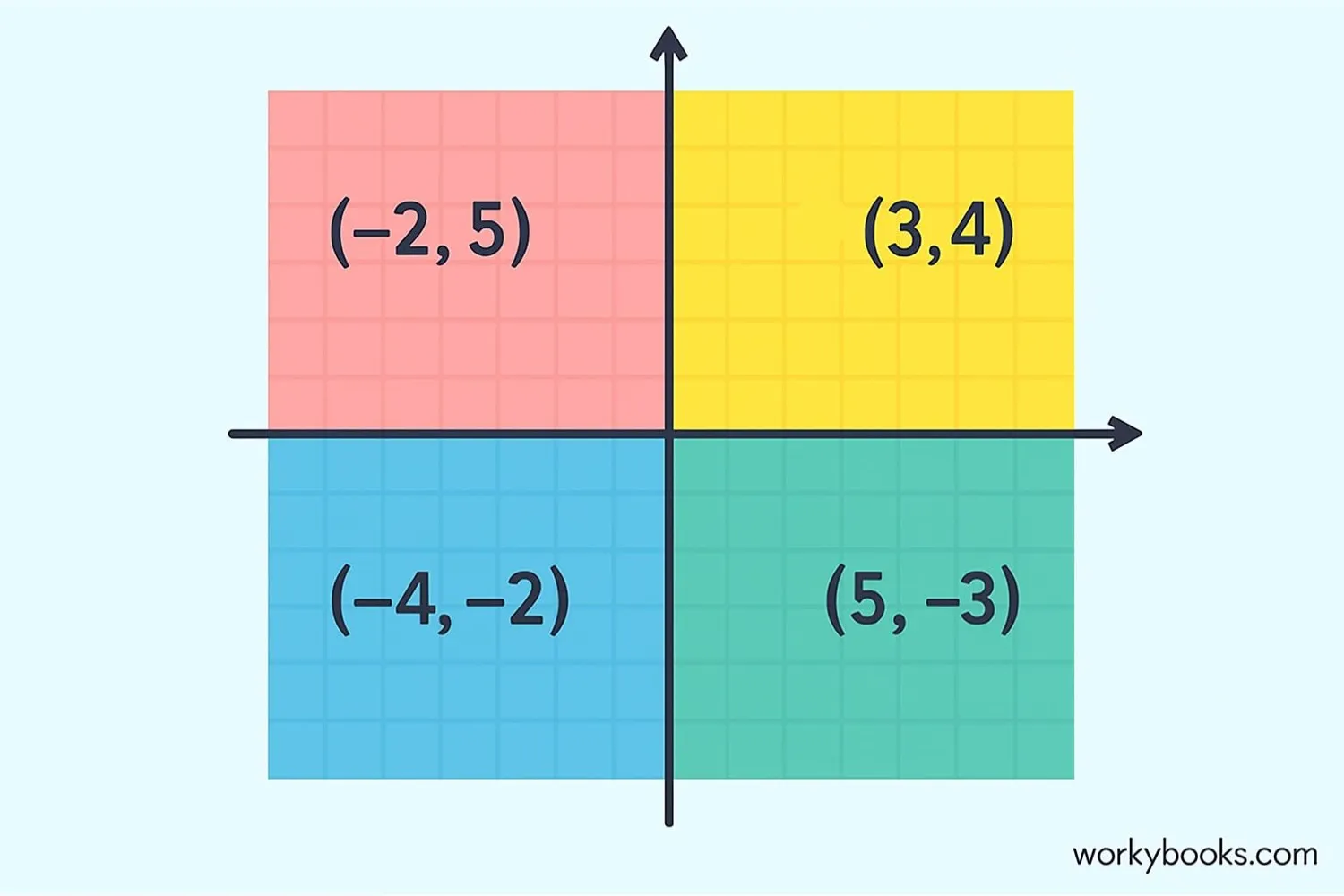
Plotting points is like giving directions to a specific location on the coordinate plane. Each point has an (x,y) coordinate:
Steps to plot a point:
1. Start at the origin (0,0)
2. Move horizontally along the x-axis (right for positive, left for negative)
3. Move vertically along the y-axis (up for positive, down for negative)
Let's practice with some examples:
Point (3,4): From (0,0), move right 3 units, then up 4 units → Quadrant I
Point (-2,5): From (0,0), move left 2 units, then up 5 units → Quadrant II
Point (-1,-3): From (0,0), move left 1 unit, then down 3 units → Quadrant III
Point (4,-2): From (0,0), move right 4 units, then down 2 units → Quadrant IV
Plotting Tip
Always check the signs of your coordinates to know which quadrant your point should be in.
Real-World Examples
Quadrants aren't just for math class! We use them in many real-world situations:
1. Map Navigation: Cities are often divided into quadrants (NW, NE, SW, SE) to help locate addresses.
2. Video Games: Game designers use quadrants to position characters and objects on the screen.
3. Weather Maps: Meteorologists use quadrants to describe storm locations ("the storm is in the northeast quadrant").
4. Architecture: Builders use coordinate systems to place elements in buildings and landscapes.
5. Navigation: Ships and airplanes use coordinate systems similar to quadrants for navigation.
Real-World Connection
Understanding quadrants helps you read maps, play video games, and even understand weather reports!
Quadrant Practice Quiz
Test your knowledge about quadrants with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about quadrants:
Math Trivia
Discover interesting facts about coordinate systems and quadrants:
Cartesian Origins
The coordinate system is named after French mathematician René Descartes. According to legend, he got the idea while watching a fly on his ceiling and wondering how to describe its position.
3D Quadrants
In three-dimensional space, there are eight octants instead of four quadrants. These are formed by adding a z-axis perpendicular to the x and y axes.
Space Navigation
NASA uses a similar coordinate system to navigate spacecraft. Their system includes quadrants to describe positions relative to Earth and other celestial bodies.
Largest Coordinate System
Astronomers use an enormous coordinate system to map the universe. The celestial coordinate system divides the sky into quadrants to locate stars, galaxies, and other objects.




