Quotient - Definition, Examples, Quiz, FAQ, Trivia
Learn about division and how to find quotients with easy explanations and practice activities
What is a Quotient?

A quotient is the result you get when you divide one number by another. It's the answer to a division problem!
Think of it like sharing cookies equally with friends. If you have 10 cookies and 5 friends, how many cookies does each friend get?
You would divide 10 by 5: 10 ÷ 5 = 2. The quotient is 2. Each friend gets 2 cookies!
Quotients help us solve problems where we need to split things into equal parts. It's one of the most useful math skills you'll learn!
Division Formula
When we divide one number (dividend) by another (divisor), we get the quotient
Division Terms
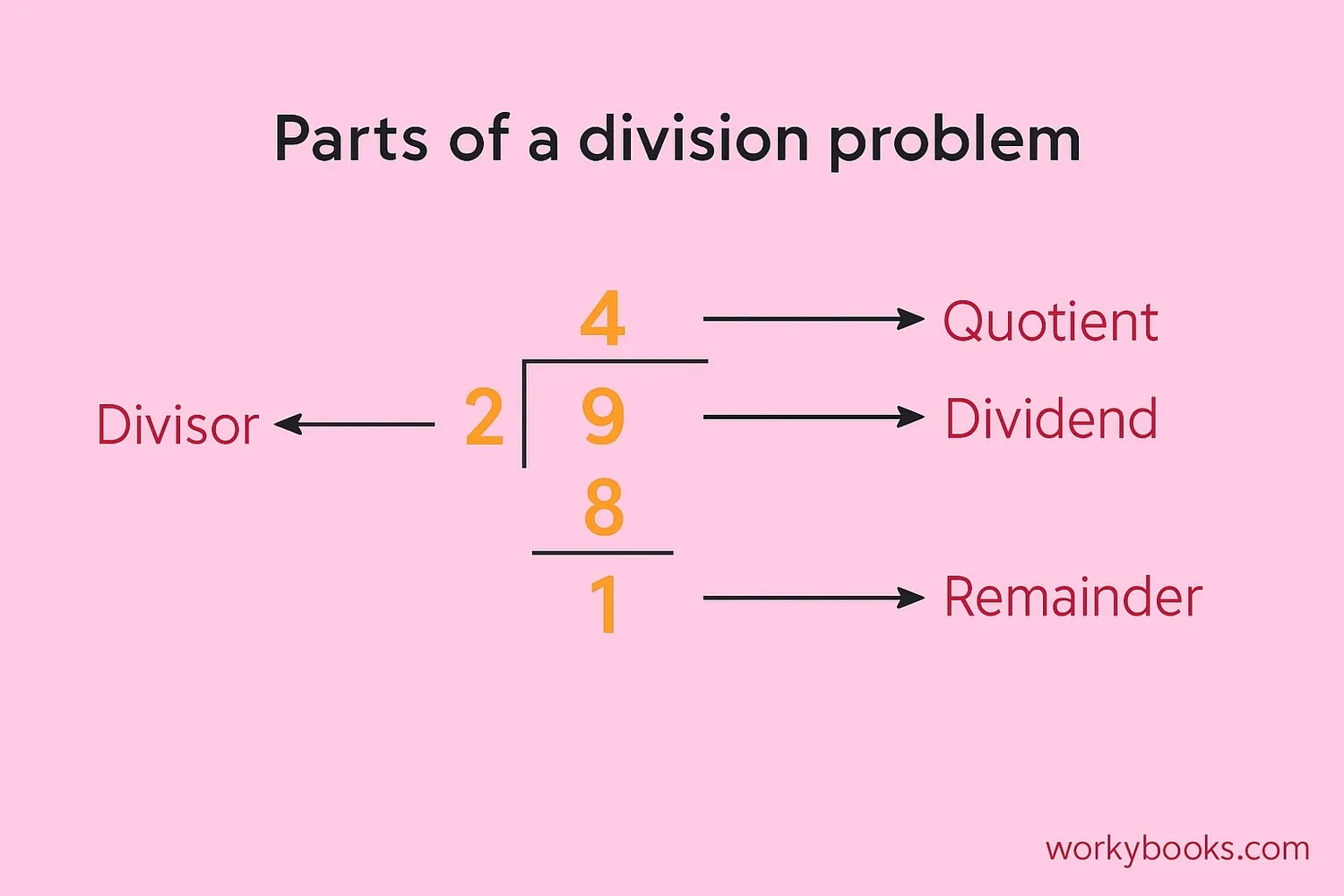
Every division problem has three important parts. Understanding these will help you solve division problems:
Dividend
The number being divided
Example: 15 ÷ 3 = 5
Divisor
The number doing the dividing
Example: 15 ÷ 3 = 5
Quotient
The result of division
Example: 15 ÷ 3 = 5
Remainder
Leftover amount
Example: 16 ÷ 3 = 5 R1
Key Concept
Remember: Dividend ÷ Divisor = Quotient. When we divide, we're splitting the dividend into equal parts determined by the divisor.
How to Find Quotients
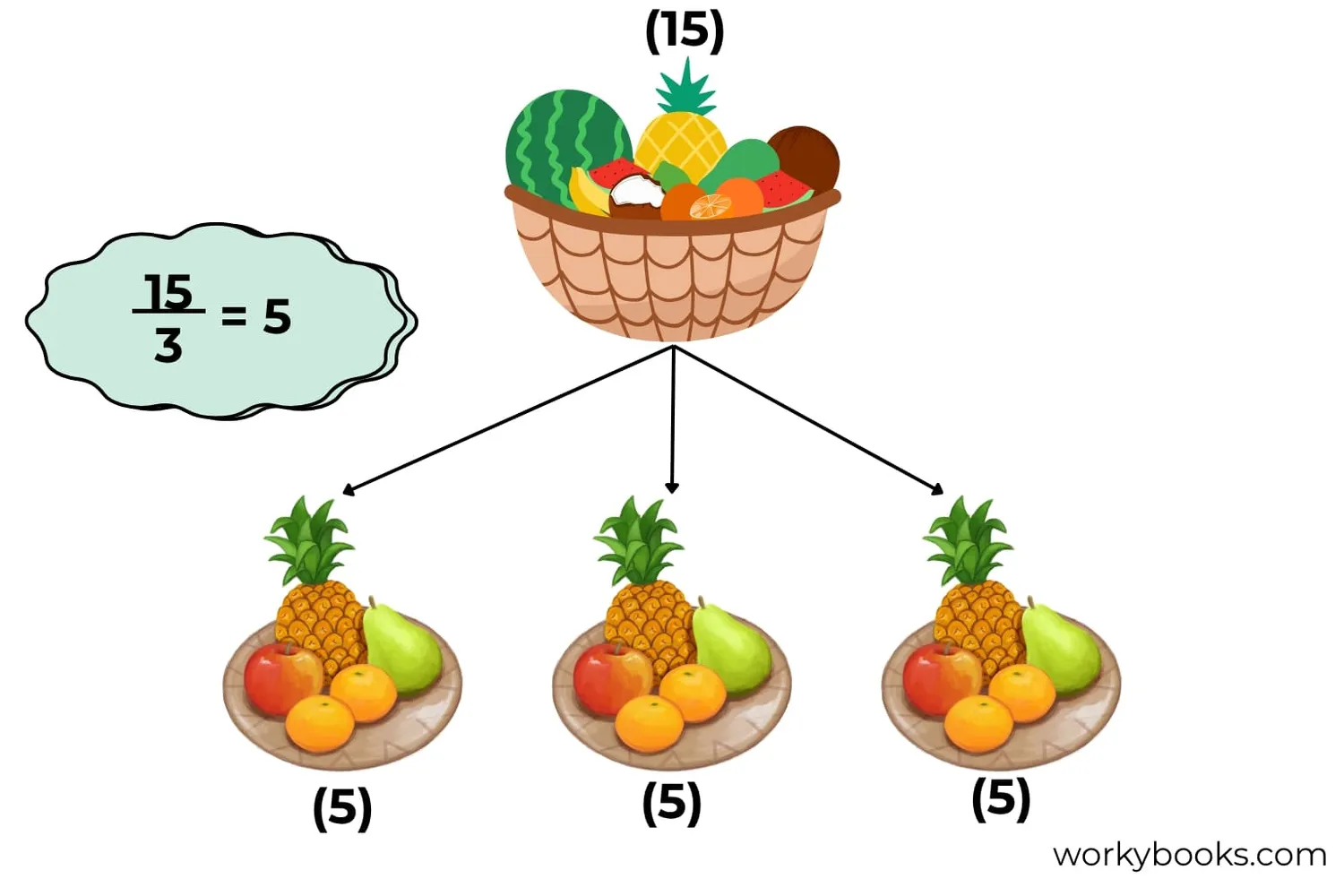
Finding quotients is like solving a puzzle. Here's how to do it step by step:
Understand the problem
What are you dividing? How many groups do you need?
Example: 15 ÷ 3 means we want to split 15 into 3 equal groups.
Use repeated subtraction
Subtract the divisor from the dividend until you can't subtract anymore.
15 - 3 = 12, 12 - 3 = 9, 9 - 3 = 6, 6 - 3 = 3, 3 - 3 = 0
We subtracted 5 times, so 15 ÷ 3 = 5
Use multiplication facts
Think: What number multiplied by the divisor equals the dividend?
3 × ? = 15 → 3 × 5 = 15, so 15 ÷ 3 = 5
Check your answer
Multiply the quotient by the divisor. It should equal the dividend.
5 × 3 = 15 → Correct!
Remember
Division is the opposite of multiplication. Knowing your multiplication facts helps you find quotients quickly!
Division with Remainders
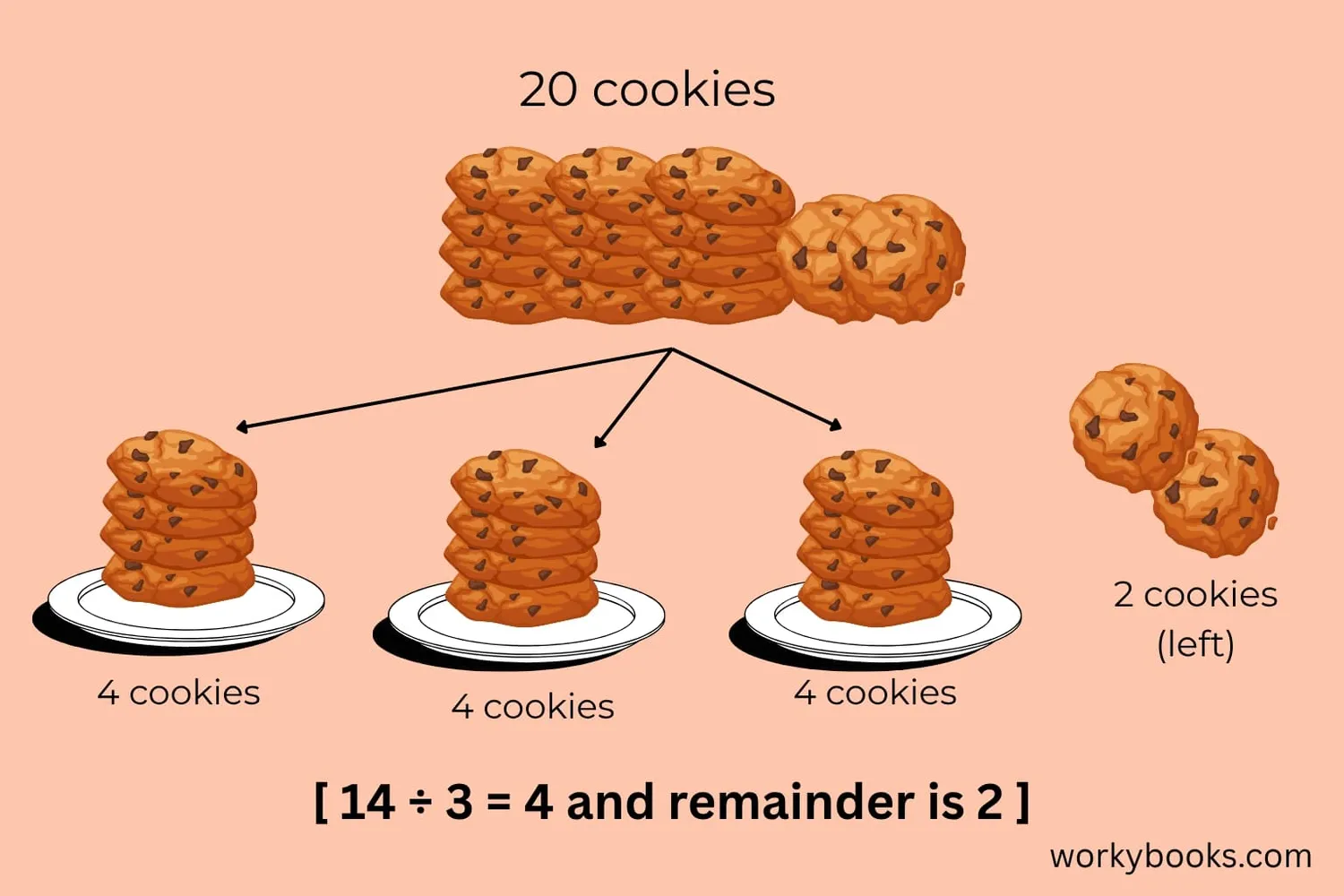
Sometimes when we divide, we have some left over. That leftover amount is called the remainder.
Example: 14 ÷ 3
3 friends want to share 14 cookies. Each friend can have 4 cookies (3 × 4 = 12). But 14 - 12 = 2, so there are 2 cookies left over.
We write this as: 14 ÷ 3 = 4 R2 (which means 4 with a remainder of 2)
Remainders happen when the dividend isn't exactly divisible by the divisor. This is very common in real life!
Division with Remainders
Example: 14 = (3 × 4) + 2
Real World
Remainders are important when sharing things that can't be divided, like cookies, people in cars, or seats at tables.
Long Division
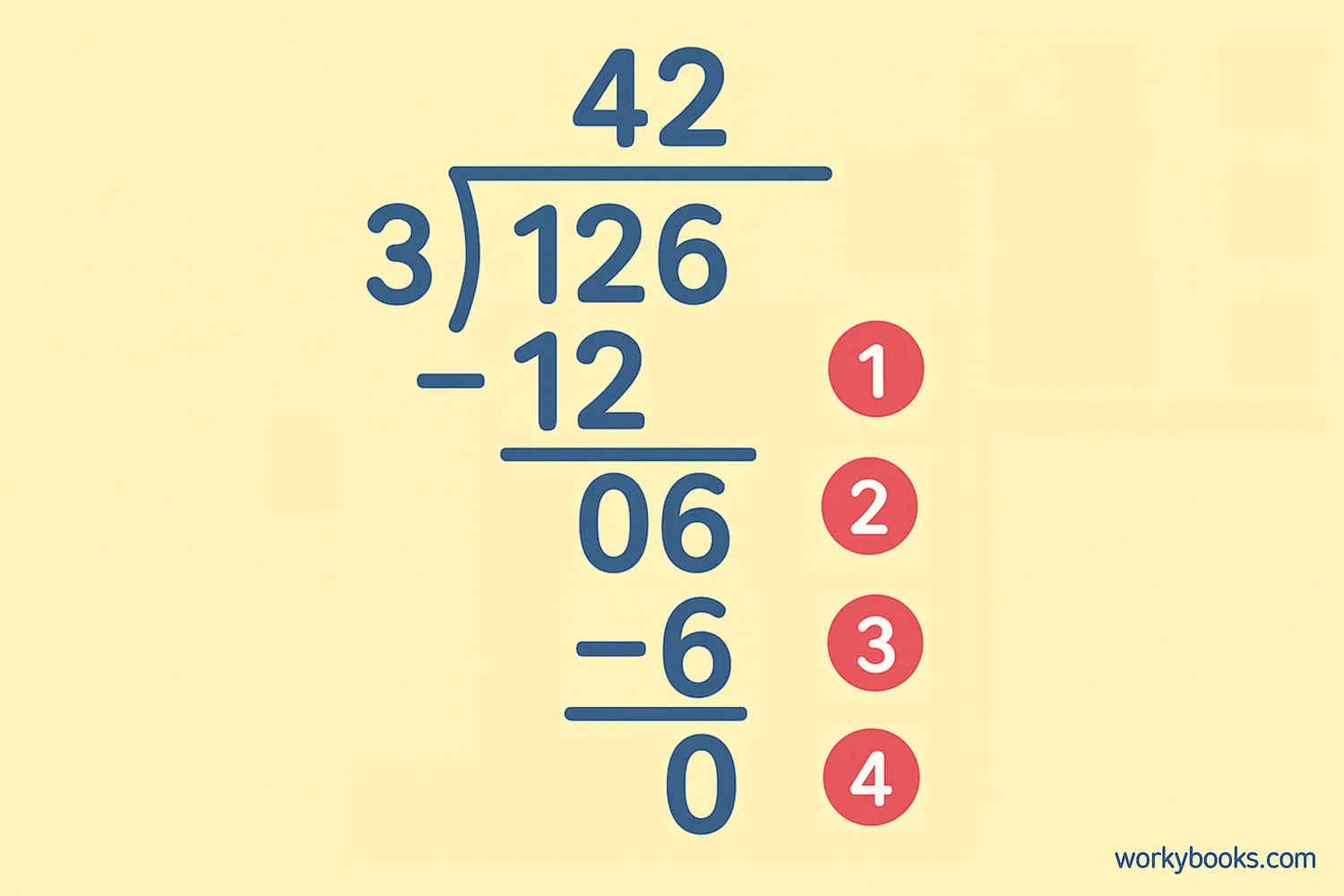
For larger numbers, we use long division. This method breaks down big division problems into smaller steps. Let's divide 126 by 3:
Set up the problem
Write the dividend (126) under the division bar and the divisor (3) outside.
Divide
How many times does 3 go into the first digit? 1 ÷ 3 = 0, so look at the first two digits: 12 ÷ 3 = 4
Multiply
Multiply 4 × 3 = 12. Write this below the 12.
Subtract
Subtract: 12 - 12 = 0
Bring down
Bring down the next digit (6) to make 06.
Repeat
6 ÷ 3 = 2. Write 2 above the division bar. Multiply 2 × 3 = 6. Subtract: 6 - 6 = 0.
Result
The quotient is 42. 126 ÷ 3 = 42
Long Division Tip
Remember the steps: Divide, Multiply, Subtract, Bring down (DMSB). Repeat until you have no more digits to bring down.
Division with Decimals
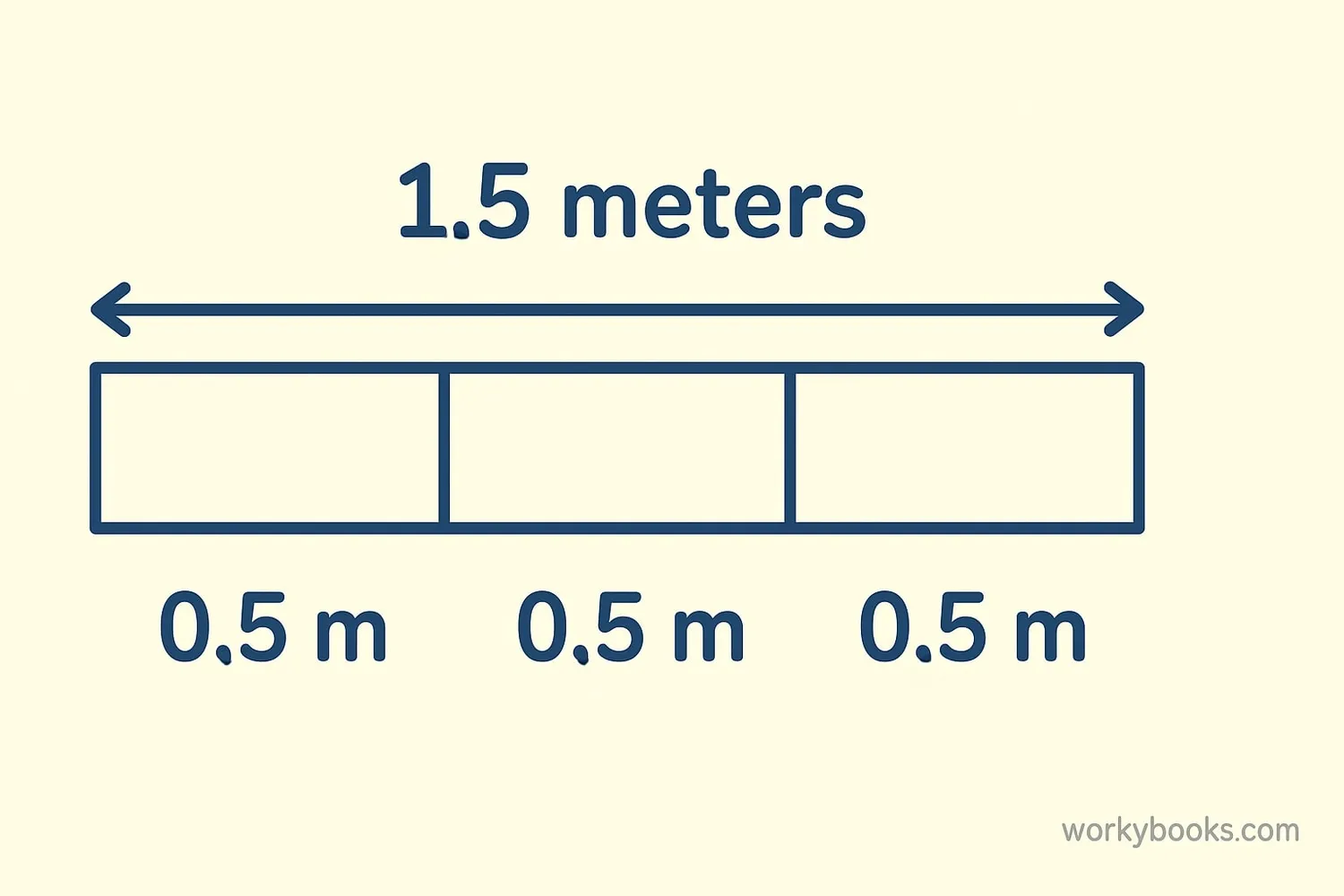
We can also find quotients when working with decimals. The process is similar to regular division, but we need to pay attention to the decimal point.
Example: 15.6 ÷ 3
Step 1: Set up the problem as regular long division: 3 ⟌ 15.6
Step 2: Divide 15 by 3 = 5. Write 5 above the division bar.
Step 3: Place the decimal point in the quotient directly above the decimal point in the dividend.
Step 4: Bring down the 6. Now divide 6 by 3 = 2. Write 2 above the division bar.
Result: 15.6 ÷ 3 = 5.2
When dividing decimals, we can make the divisor a whole number by moving the decimal point in both numbers:
Example: 4.5 ÷ 0.5 = 45 ÷ 5 = 9
Remember
When dividing decimals, move the decimal point in the divisor to make it a whole number, then move the decimal point in the dividend the same number of places.
Quotient Practice Quiz
Test your division knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about quotients and division:
Math Trivia
Discover interesting facts about division and mathematics:
Ancient Division
The oldest known division algorithm comes from ancient Egypt around 2000 BC. Egyptians used a method called "doubling" to perform division.
Division Symbol
The division symbol (÷) is called an obelus. It was first used by Swiss mathematician Johann Rahn in 1659 in his book Teutsche Algebra.
Computer Division
Computers perform division using special algorithms since division is more complex than multiplication. Some processors use the "Newton-Raphson" method for division.
Largest Division Problem
The largest division problem ever solved involved numbers with over 2 billion digits! It took supercomputers several weeks to complete the calculation.





