Radians to Degrees - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert between radian and degree angle measurements with easy explanations and practice activities
What are Radians & Degrees?
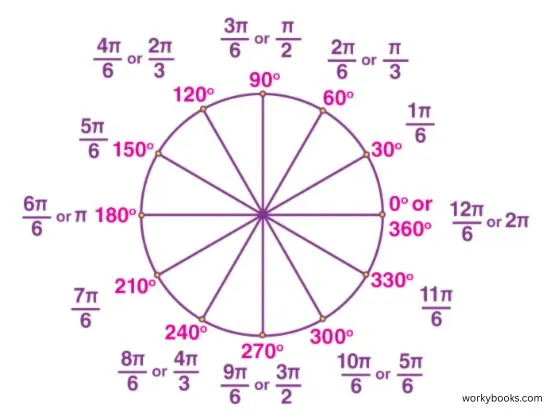
Angles can be measured in two common units: degrees and radians.
Degrees are the more familiar unit. A full circle is divided into 360 equal parts, each part being 1 degree (1°).
Radians are based on the radius of the circle. One radian is the angle created when the arc length is exactly equal to the radius of the circle. A full circle has 2π radians (about 6.28 radians).
Why do we need both? Degrees are great for everyday measurements, while radians are especially useful in higher mathematics and physics because they simplify many formulas.
Key Concept
π (pi) radians = 180 degrees. This relationship is the foundation for all radian-to-degree conversions.
How to Convert Radians to Degrees
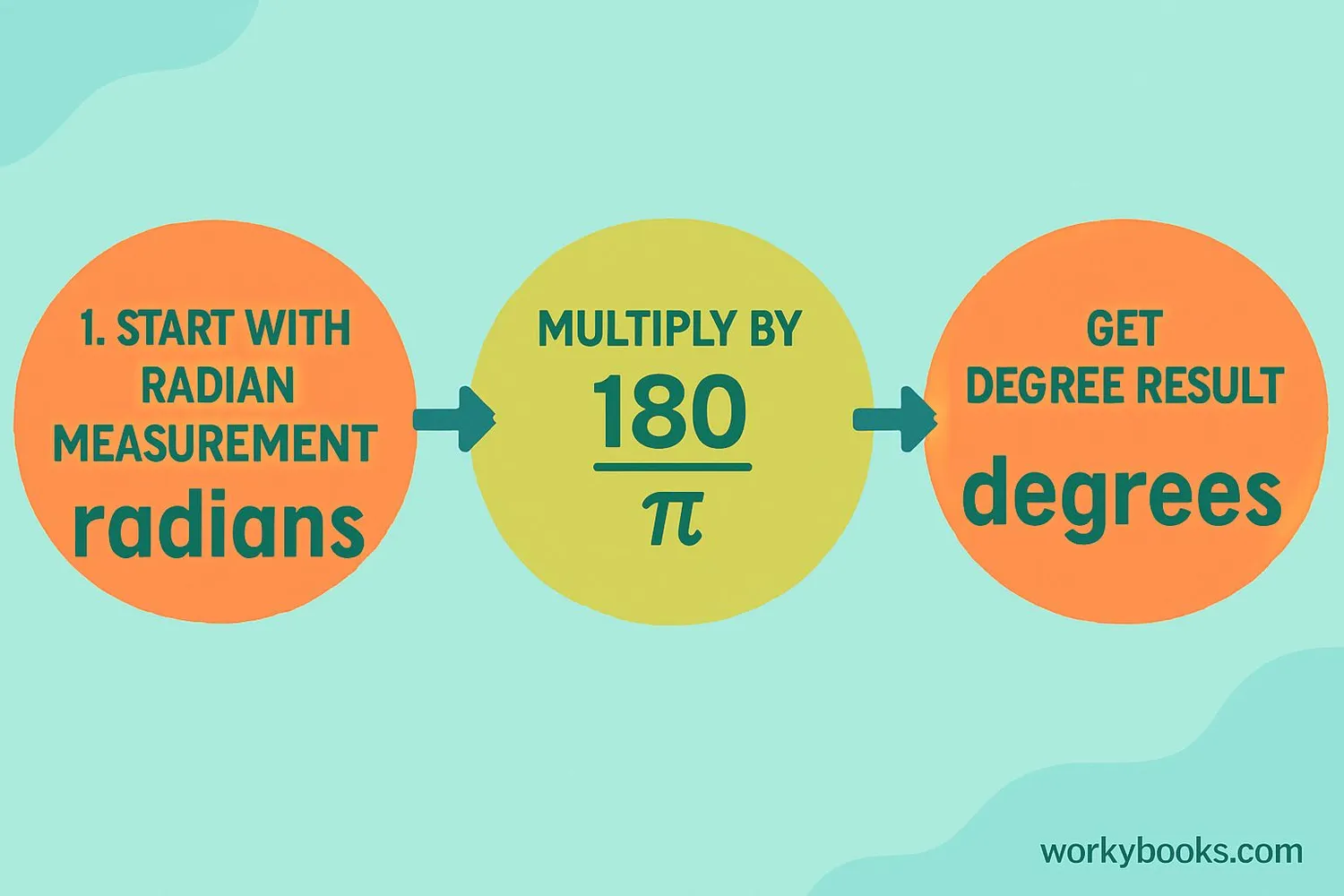
Converting radians to degrees is simple once you remember the conversion factor:
Conversion Formula
To convert any measurement in radians to degrees, multiply the number of radians by 180 divided by π (approximately 3.14159).
Example: Convert π/2 radians to degrees
Step 1: Start with the measurement in radians → π/2 rad
Step 2: Multiply by 180/π → (π/2) × (180/π)
Step 3: Simplify → π cancels out: (1/2) × 180 = 90°
So π/2 radians equals 90 degrees. That's a right angle!
Remember
The constant π (pi) is approximately 3.14159, but you can often leave it as π in calculations for exact values.
Radians to Degrees Conversion Charts

Conversion charts help us quickly find equivalent angle measurements without calculating each time. Here are useful charts for converting radians to degrees:
Common Radians to Degrees Conversion Chart
| Radians (rad) | Degrees (°) |
|---|---|
| 0 | 0° |
| π/6 ≈ 0.5236 | 30° |
| π/4 ≈ 0.7854 | 45° |
| π/3 ≈ 1.0472 | 60° |
| π/2 ≈ 1.5708 | 90° |
| 2π/3 ≈ 2.0944 | 120° |
| 3π/4 ≈ 2.3562 | 135° |
| 5π/6 ≈ 2.6180 | 150° |
| π ≈ 3.1416 | 180° |
| 3π/2 ≈ 4.7124 | 270° |
| 2π ≈ 6.2832 | 360° |
Special Angles Conversion Chart
| Angle | Radians | Degrees |
|---|---|---|
| Full circle | 2π | 360° |
| Half circle | π | 180° |
| Quarter circle | π/2 | 90° |
| Eighth circle | π/4 | 45° |
| Sixth circle | π/3 | 60° |
| Twelfth circle | π/6 | 30° |
Chart Tip
Notice how each multiple of π radians corresponds to a multiple of 180 degrees? This pattern can help you estimate conversions!
Real-World Examples

Let's practice conversion with some real-world examples:
Example 1: A right angle is π/2 radians. What is this in degrees?
Solution: (π/2) × (180/π) = 180/2 = 90°
Example 2: A straight angle is π radians. What is this in degrees?
Solution: π × (180/π) = 180°
Example 3: A circle has 2π radians. How many degrees is this?
Solution: 2π × (180/π) = 360°
Example 4: Convert 1.5 radians to degrees (use π ≈ 3.1416)
Solution: 1.5 × (180/π) ≈ 1.5 × (180/3.1416) ≈ 1.5 × 57.3 ≈ 85.95°
Practice converting angles you see around you - the corner of a book, the hands of a clock, or a slice of pizza!
Conversion Tip
To convert degrees back to radians, multiply by π/180 instead of dividing.
Conversion Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about radians and degrees conversion:
Math Trivia
Discover interesting facts about angle measurement:
Origin of Radians
The concept of the radian was first introduced by mathematician Roger Cotes in 1714, though the term "radian" itself wasn't used until 1873. The word "radian" comes from "radius," highlighting its relationship to a circle's radius.
Why 360 Degrees?
The ancient Babylonians used a base-60 number system and divided a circle into 360 parts. This division was practical because 360 has many divisors, making it convenient for calculations and astronomy.
Radians in Space
NASA and other space agencies use radians for spacecraft navigation because radians provide more precise measurements for the vast distances and angles involved in space travel.
Pi Connection
The relationship between radians and degrees depends on π (pi). The exact conversion factor is 180/π, which is approximately 57.2958 degrees per radian. This makes π fundamental to angle conversion.





