Rational Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn about fractions, decimals, and ratios with easy explanations and practice activities
What Are Rational Numbers?
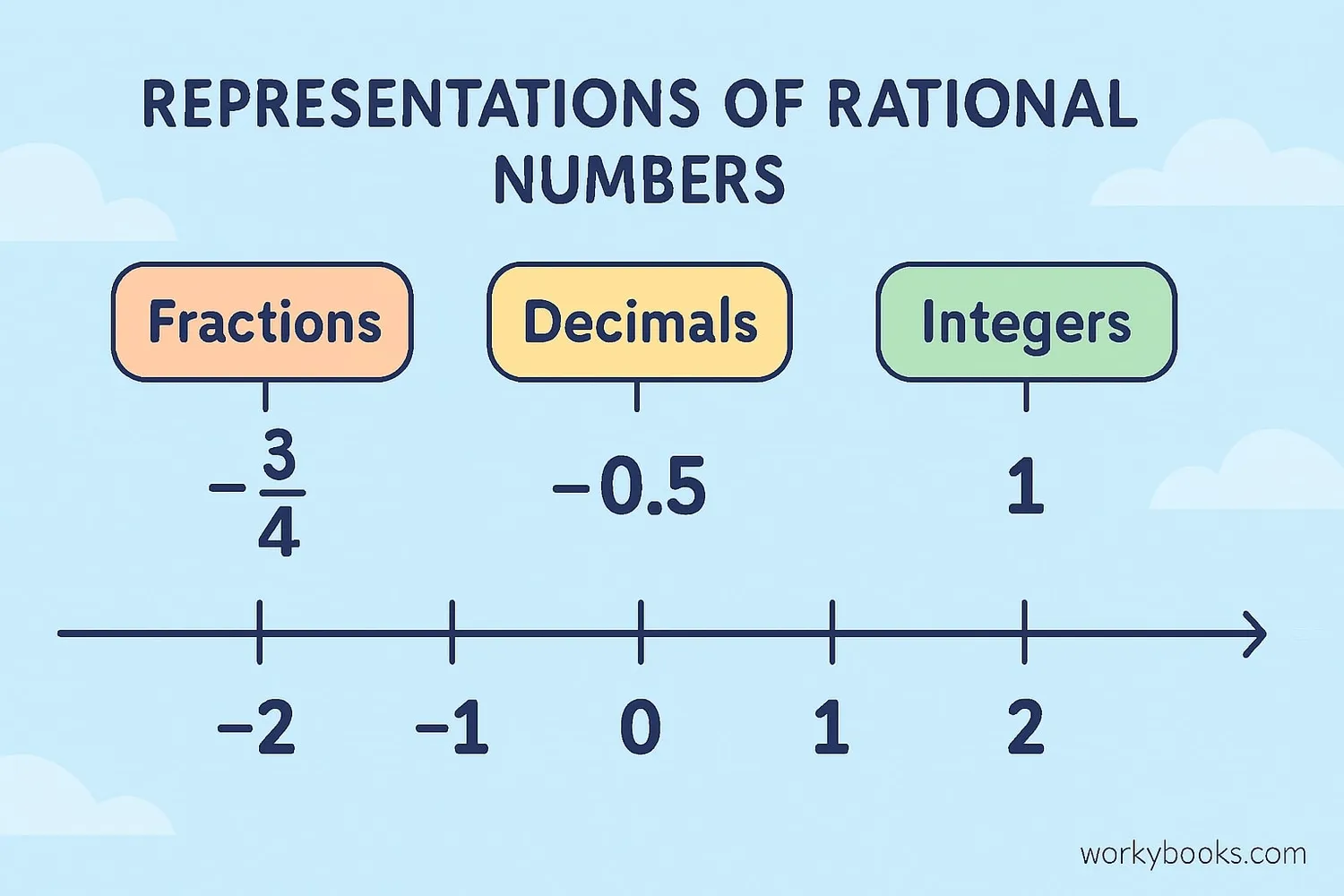
Rational numbers are numbers that can be written as a fraction where both the numerator (top number) and denominator (bottom number) are integers, and the denominator is not zero.
This means rational numbers include:
- All integers (like 5, -3, 0)
- Fractions (like 1/2, 3/4, 7/5)
- Terminating decimals (like 0.5, 3.75)
- Repeating decimals (like 0.333..., 1.272727...)
Rational numbers are like "ratio numbers" because they represent a ratio of two integers. They help us express parts of a whole and measurements that aren't whole numbers.
Key Concept
A number is rational if it can be written as a fraction a/b where a and b are integers and b ≠ 0.
Identifying Rational Numbers

How can you tell if a number is rational? Here's a simple way to check:
Step 1: Can the number be written as a fraction?
Step 2: Is the denominator not zero?
If both answers are yes, then it's a rational number!
Let's look at some examples:
- 5 is rational because it can be written as 5/1
- 0.25 is rational because it equals 1/4
- 0.333... is rational because it equals 1/3
- 2/3 is rational (it's already a fraction)
- √2 is NOT rational (it can't be written as a fraction of integers)
- π is NOT rational (it's a non-repeating, non-terminating decimal)
Remember
All fractions are rational numbers, but not all rational numbers are fractions - they can also be integers or decimals!
Real-World Examples

Rational numbers are all around us! Here are some real-world examples:
Food Fractions
When you eat 3 slices of an 8-slice pizza, you've eaten 3/8 of the pizza - a rational number!
Measurements
A pencil might be 5.5 inches long - that's 11/2 inches, a rational number.
Time
Half past 3 is 3:30, which can be written as 3.5 hours - a rational number.
Money
$1.50 is the same as 3/2 or 150/100 dollars - both rational numbers.
Math Tip
Any measurement you make with a ruler or measuring cup will be a rational number because you're using fractions of units.
Operations with Rational Numbers
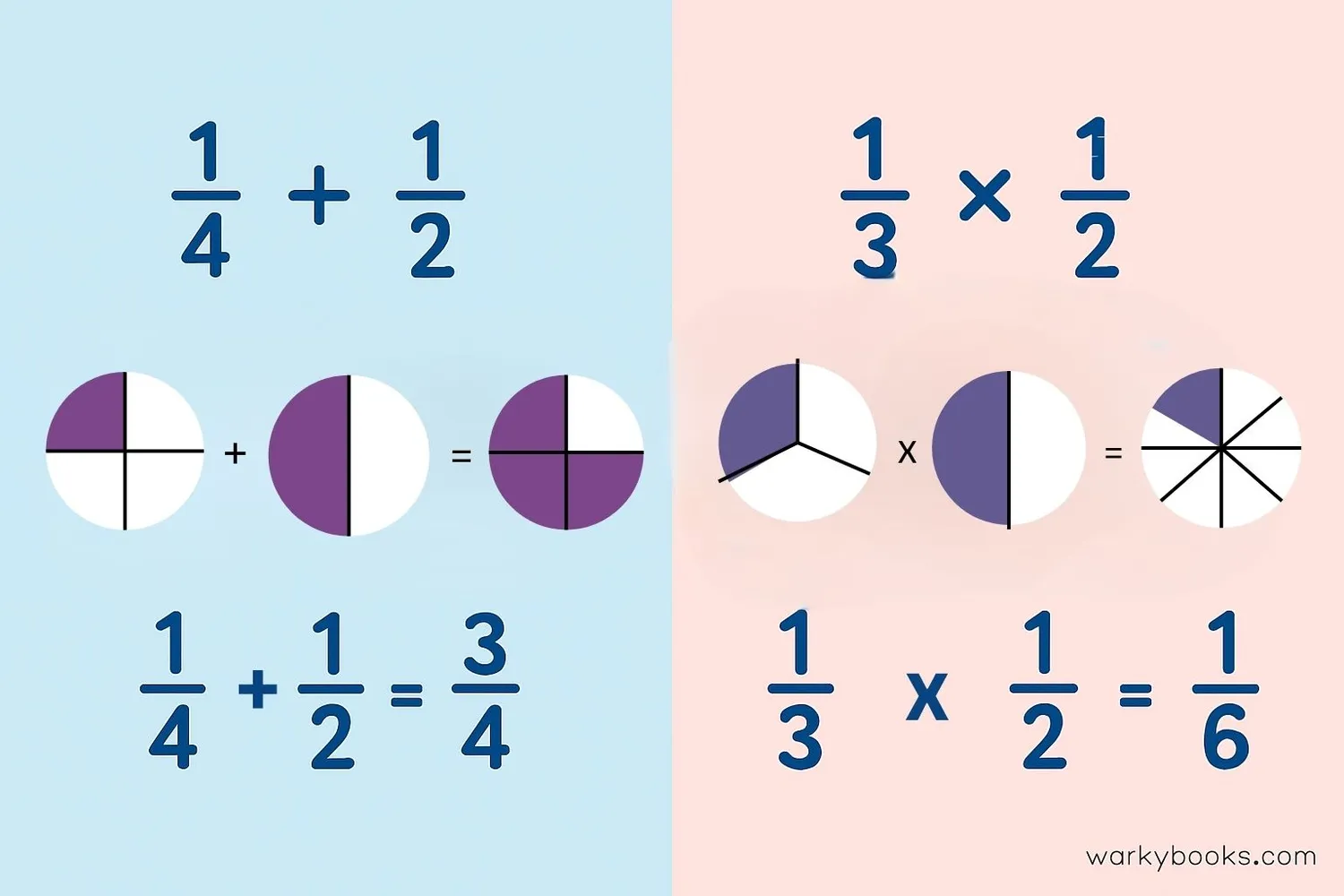
We can add, subtract, multiply, and divide rational numbers just like other numbers. Here's how:
Adding/Subtracting Fractions:
1. Find a common denominator
2. Add/subtract the numerators
3. Simplify the result
Example: 1/4 + 1/2 = 1/4 + 2/4 = 3/4
Multiplying Fractions:
1. Multiply numerators together
2. Multiply denominators together
3. Simplify the result
Example: 1/3 × 1/2 = (1×1)/(3×2) = 1/6
Dividing Fractions:
1. Flip the second fraction (find its reciprocal)
2. Multiply the fractions
3. Simplify the result
Example: 1/2 ÷ 1/4 = 1/2 × 4/1 = 4/2 = 2
Key Rules
Rational Numbers Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about rational numbers:
Math Trivia
Discover interesting facts about numbers and mathematics:
Ancient Fractions
The ancient Egyptians used fractions over 4,000 years ago! They had special symbols for fractions like 1/2, 1/3, and 1/4, and wrote all other fractions as sums of these unit fractions.
Golden Ratio
The golden ratio (approximately 1.618) is a special irrational number that appears in nature, art, and architecture. It's found in seashells, flower petals, and even in the proportions of the human body!
Rational Numbers in Computers
Computers store rational numbers using fractions! They represent numbers as binary fractions (base 2) to perform calculations accurately and efficiently.
Infinite Fractions
The fraction 1/3 is a rational number, but its decimal form 0.333... goes on forever! All rational numbers either terminate (like 1/4 = 0.25) or repeat (like 1/6 = 0.1666...).





