Reciprocal of Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn how to find the reciprocal of fractions with simple explanations and practice activities
What is a Reciprocal?
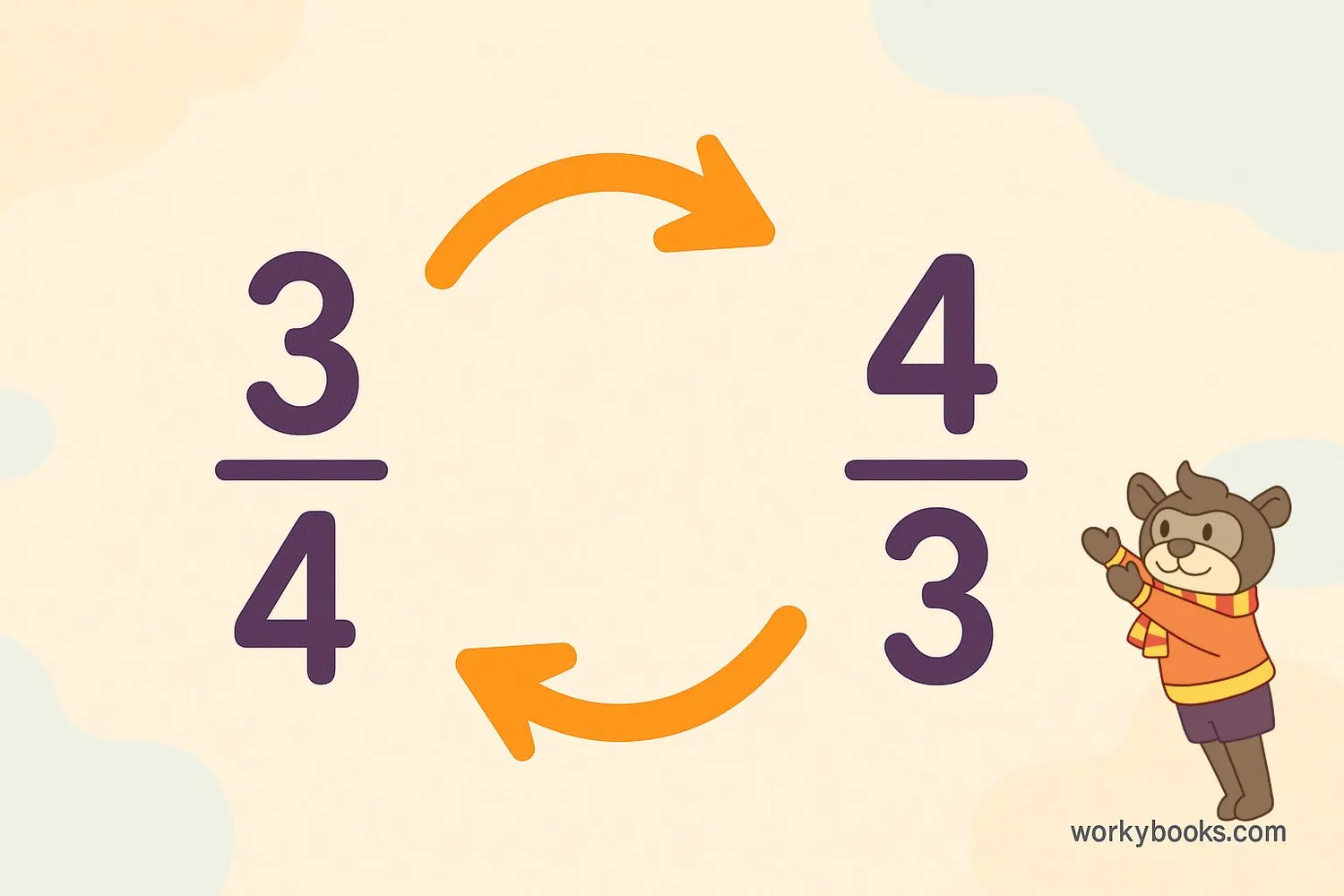
The reciprocal of a fraction is a special number that when multiplied by the original fraction, gives 1. It's also called the multiplicative inverse.
To find the reciprocal of a fraction, you simply swap the numerator and denominator. For example:
Why is this useful? When you multiply a fraction by its reciprocal, you always get 1:
3/4 × 4/3 = 12/12 = 1
Key Concept
Reciprocal means "flipping" the fraction. It's the multiplicative inverse that gives 1 when multiplied by the original fraction.
How to Find the Reciprocal
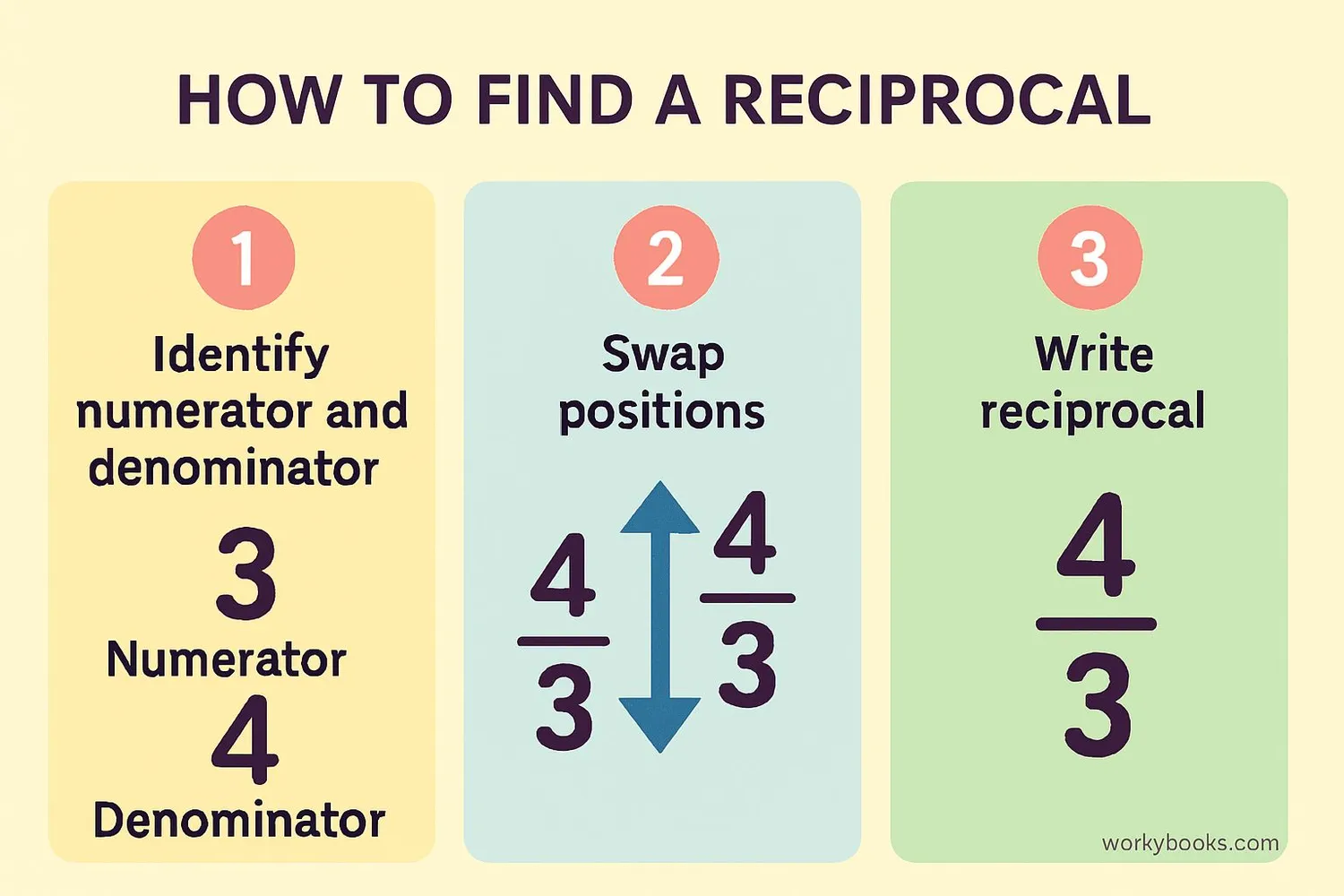
Finding the reciprocal of a fraction is simple when you follow these steps:
Reciprocal Formula
Swap the numerator (top number) and denominator (bottom number)
Let's practice with examples:
Example 1: Reciprocal of 2/5 is 5/2
Example 2: Reciprocal of 7/9 is 9/7
Example 3: Reciprocal of 1/4 is 4/1 = 4
What about whole numbers? Every whole number has a denominator of 1:
Example 4: Reciprocal of 5 (which is 5/1) is 1/5
Remember
The reciprocal of a fraction is always another fraction (unless it's a whole number).
Reciprocal of Mixed Fractions
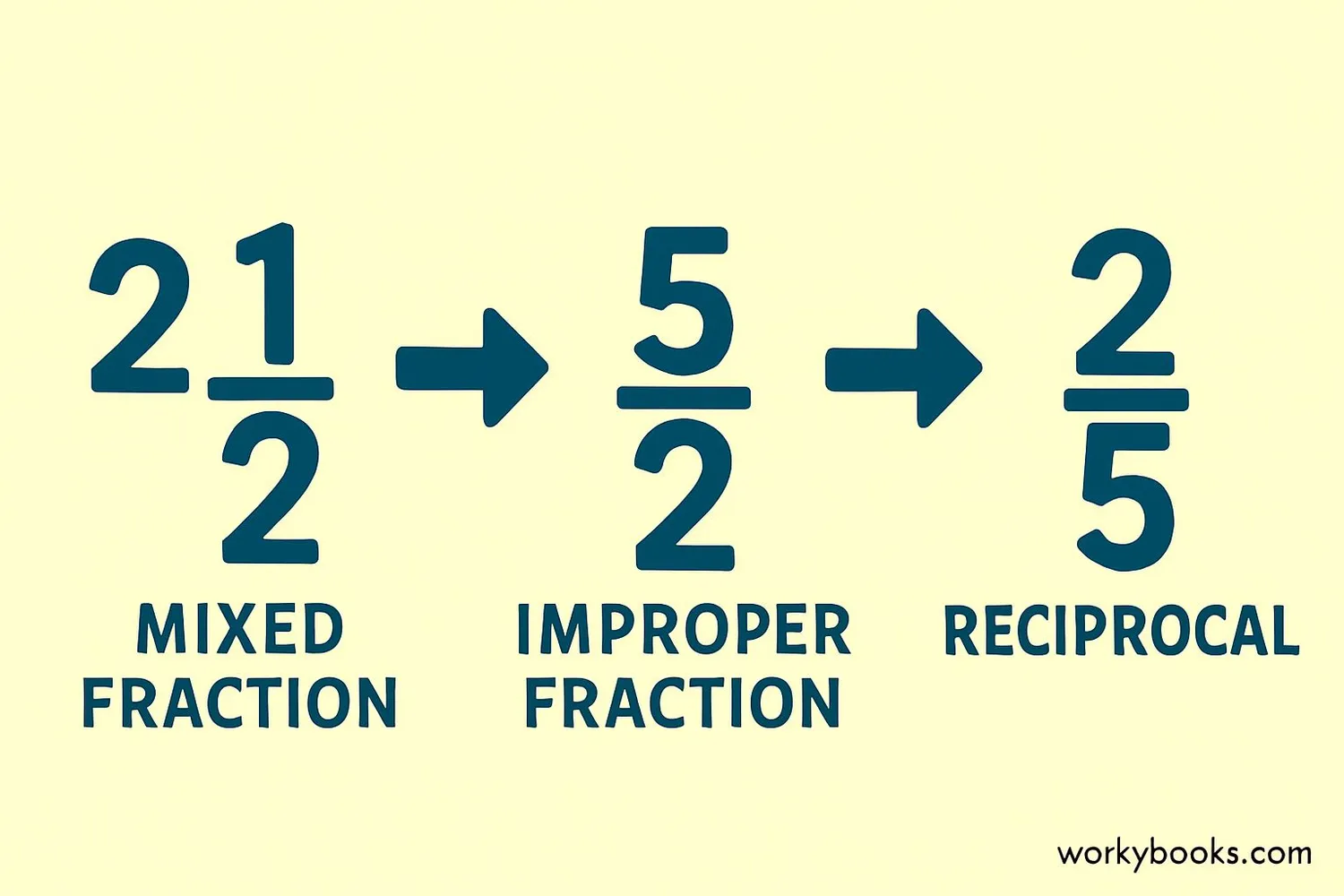
To find the reciprocal of a mixed fraction, we first need to convert it to an improper fraction. Here's how:
Mixed Fraction
Whole number + fraction
Convert to Improper
(2 × 2) + 1 = 5
Reciprocal
Swap numerator and denominator
Step-by-step process:
1. Convert the mixed number to an improper fraction
2. Swap the numerator and denominator
3. Simplify if possible
Example: Find reciprocal of 3 1/3
Step 1: Convert to improper fraction → (3 × 3) + 1 = 10/3
Step 2: Swap numerator and denominator → 3/10
So reciprocal of 3 1/3 is 3/10
Reciprocal of Negative Fractions

The reciprocal of a negative fraction is also negative. The process is the same as for positive fractions:
Example 1: Reciprocal of -2/5 is -5/2
Example 2: Reciprocal of -3/7 is -7/3
Important rule: When you multiply a negative fraction by its reciprocal, you still get 1:
-2/5 × -5/2 = 10/10 = 1
Remember
The negative sign stays with the fraction. When you flip the fraction, the negative sign moves with the numbers.
Reciprocal of Unit Fractions
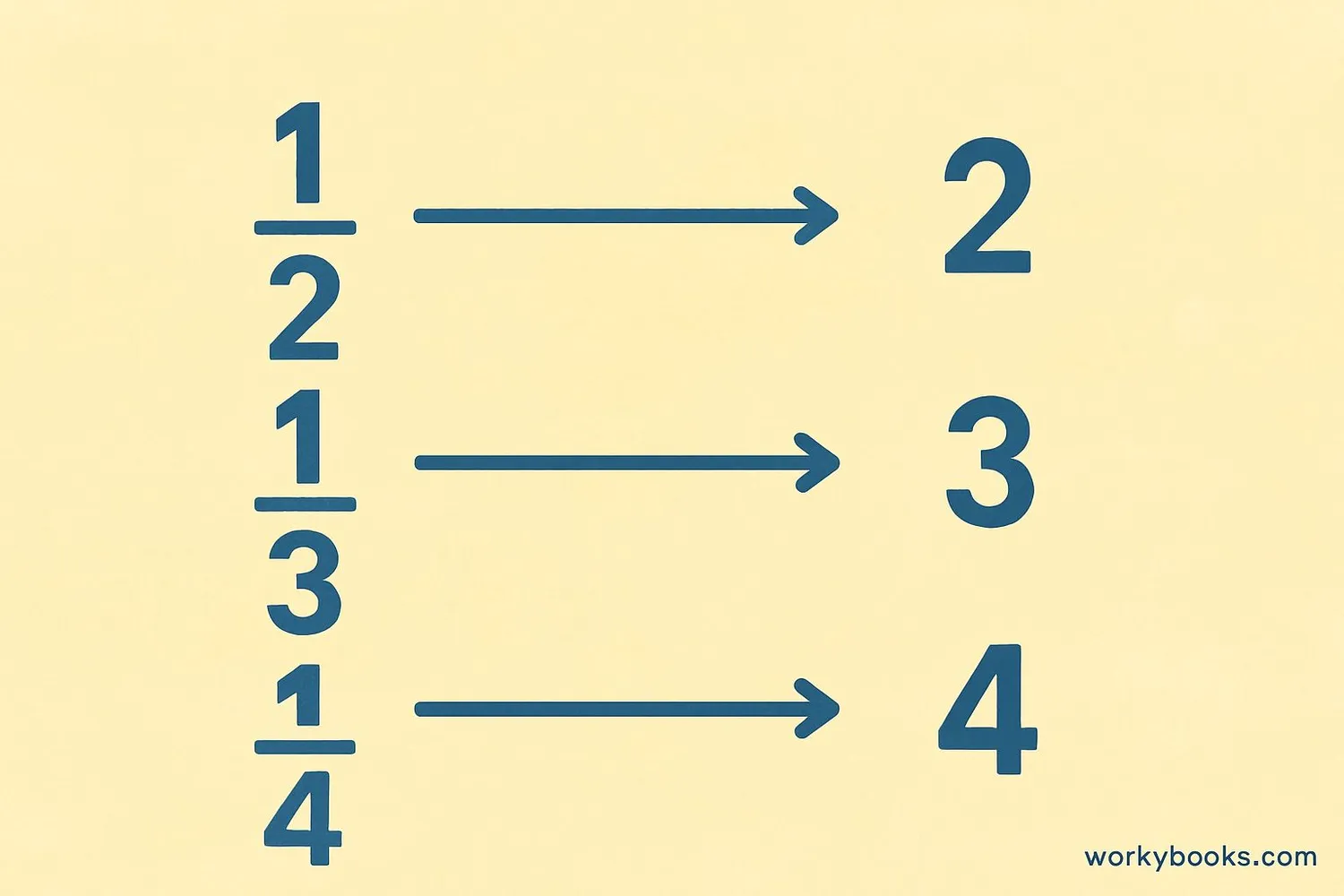
Unit fractions have 1 as the numerator. Their reciprocals are special because they become whole numbers:
Example 1: Reciprocal of 1/5 is 5/1 = 5
Example 2: Reciprocal of 1/8 is 8/1 = 8
Example 3: Reciprocal of 1/100 is 100/1 = 100
This pattern makes unit fractions easy to work with! The reciprocal of any unit fraction 1/n is simply n.
Conversion Tip
Unit fractions have the simplest reciprocals - just the denominator becomes a whole number!
Reciprocal Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about fraction reciprocals:
Fraction Trivia
Discover interesting facts about fractions and reciprocals:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC, but they only used unit fractions (fractions with numerator 1). They would write other fractions as sums of unit fractions.
Reciprocal in Music
In music, reciprocals appear in rhythm. If a whole note lasts 4 beats, a half note is 1/2 (2 beats), a quarter note is 1/4 (1 beat), and so on. The reciprocal relationship determines note durations.
Golden Ratio
The golden ratio (approximately 1.618) has a special reciprocal property. Its reciprocal is exactly one less than itself: 1/1.618 ≈ 0.618 = 1.618 - 1. This appears in art, architecture, and nature.
Infinite Reciprocals
The reciprocal of a very small fraction is a very large number. For example, the reciprocal of 1/1,000,000 is 1,000,000. As fractions get closer to zero, their reciprocals approach infinity!





