Remainders - Definition, Examples, Quiz, FAQ, Trivia
Learn about division remainders with step-by-step explanations and practice activities
What is a Remainder?

A remainder is what's left over when we divide one number by another. Sometimes numbers don't divide evenly, and we have some amount left over. That leftover part is called the remainder.
Think about sharing cookies with friends. If you have 7 cookies and 3 friends, each friend gets 2 cookies, but there's 1 cookie left over. That 1 cookie is the remainder!
In math terms:
• Dividend: The number being divided (7 cookies)
• Divisor: The number we're dividing by (3 friends)
• Quotient: The result of division (2 cookies each)
• Remainder: What's left over (1 cookie)
Division Formula
For example: 7 = (3 × 2) + 1
Key Concept
The remainder is always smaller than the divisor. If you have a remainder that's larger than the divisor, that means you can divide again!
How to Find Remainders
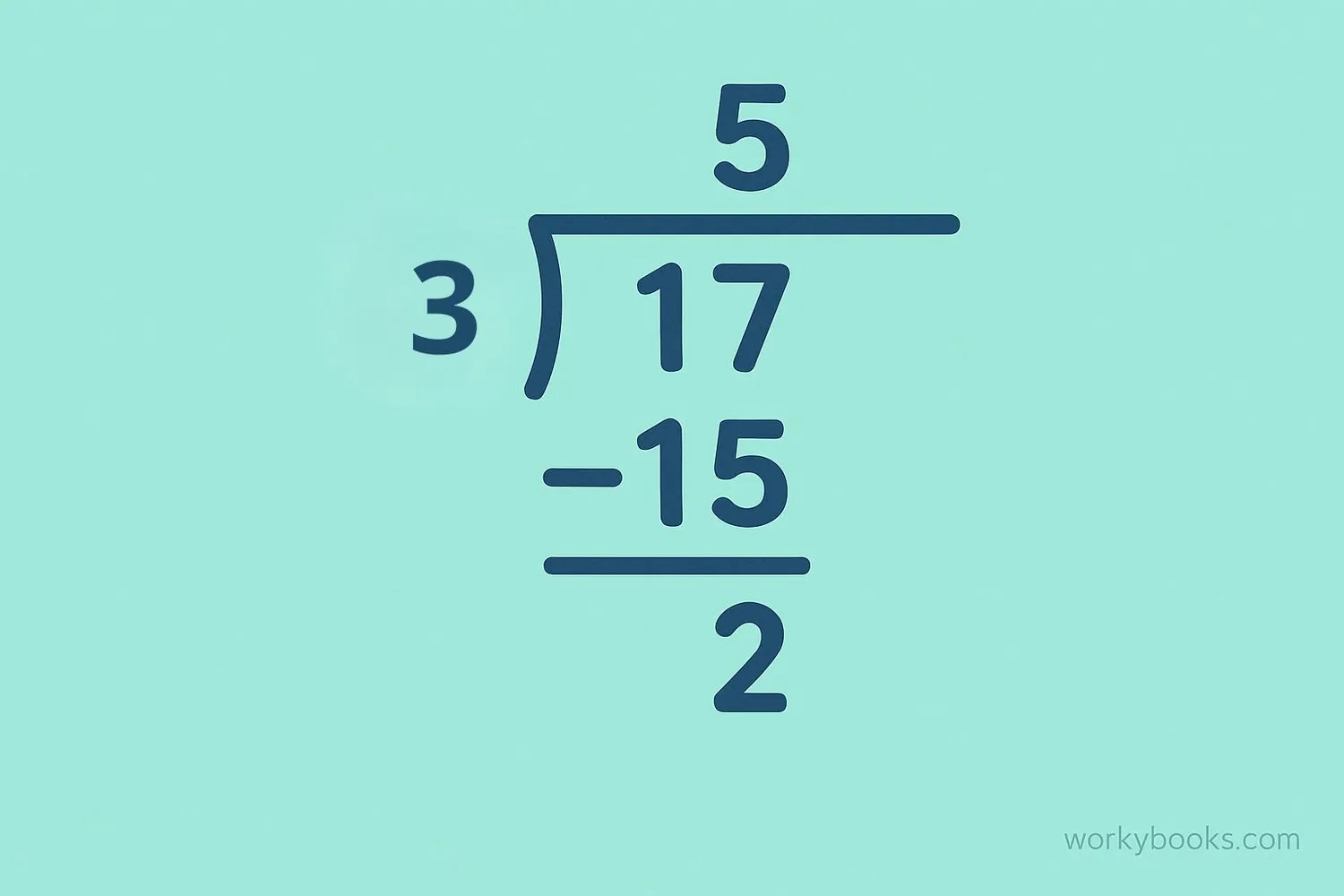
There are several ways to find remainders. Let's explore two common methods:
Method 1: Repeated Subtraction
Method 2: Long Division
Remember
In long division, the remainder is always written with an "R" before it: 17 ÷ 3 = 5 R 2
Properties of Remainders

Remainders have some special properties that help us understand division better:
Important Rules:
- The remainder is always less than the divisor
- If the remainder is zero, the dividend is divisible by the divisor
- Remainders can be added, subtracted, and multiplied with special rules
- The modulo operation (%) in programming gives the remainder
Math Tip
When dividing by 10, the remainder is always the last digit of the number!
Real-World Examples

Let's practice with some real-world examples:
Example 1: Sarah has 23 stickers. She puts them in books with 5 stickers per book. How many books can she fill? How many stickers are left?
Solution: 23 ÷ 5 = 4 R 3 → 4 full books with 3 stickers left
Example 2: There are 35 students going on a field trip. Each bus can carry 8 students. How many buses are needed?
Solution: 35 ÷ 8 = 4 R 3 → 5 buses needed (since 4 buses would leave 3 students without a ride)
Example 3: A baker has 60 cookies. She packs them into boxes of 12. How many boxes can she fill?
Solution: 60 ÷ 12 = 5 → 5 boxes with no remainder
Example 4: Tom has 47 inches of ribbon. He needs pieces that are 6 inches long. How many pieces can he cut? How much ribbon is left?
Solution: 47 ÷ 6 = 7 R 5 → 7 pieces with 5 inches left
Practice Tip
Look for division problems in your daily life - sharing snacks, grouping toys, or dividing time!
Remainder Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about remainders:
Math Trivia
Discover interesting facts about remainders and division:
Ancient Division
The concept of remainders dates back to ancient civilizations. The Egyptians used remainders in their fraction system around 2000 BCE, while the Babylonians had sophisticated division methods with remainders.
Remainder Theorem
The Remainder Theorem in algebra states that when a polynomial is divided by (x - c), the remainder is equal to the value of the polynomial at x = c. This powerful theorem connects division with function evaluation.
Computer Remainders
In computer programming, remainders are used for many tasks: checking if a number is even (n % 2 == 0), creating repeating patterns, and distributing work evenly across multiple processors.
Calendar Remainders
Our calendar uses remainders! A year has 365 days, which is 52 weeks plus 1 day (365 ÷ 7 = 52 R 1). This extra day is why your birthday moves to the next day of the week each year.


