Rhombus - Definition, Examples, Quiz, FAQ, Trivia
Learn about this special quadrilateral with easy explanations, properties, formulas, and practice activities
What is a Rhombus?

A rhombus is a special type of quadrilateral (four-sided shape) where all four sides have the same length. It looks like a squished square or a diamond shape!
Here are the key facts about a rhombus:
- It has four sides of equal length
- Opposite sides are parallel to each other
- Opposite angles are equal
- It's a special type of parallelogram
Key Concept
A rhombus is a quadrilateral with four equal sides. It's sometimes called a diamond shape!
Properties of a Rhombus
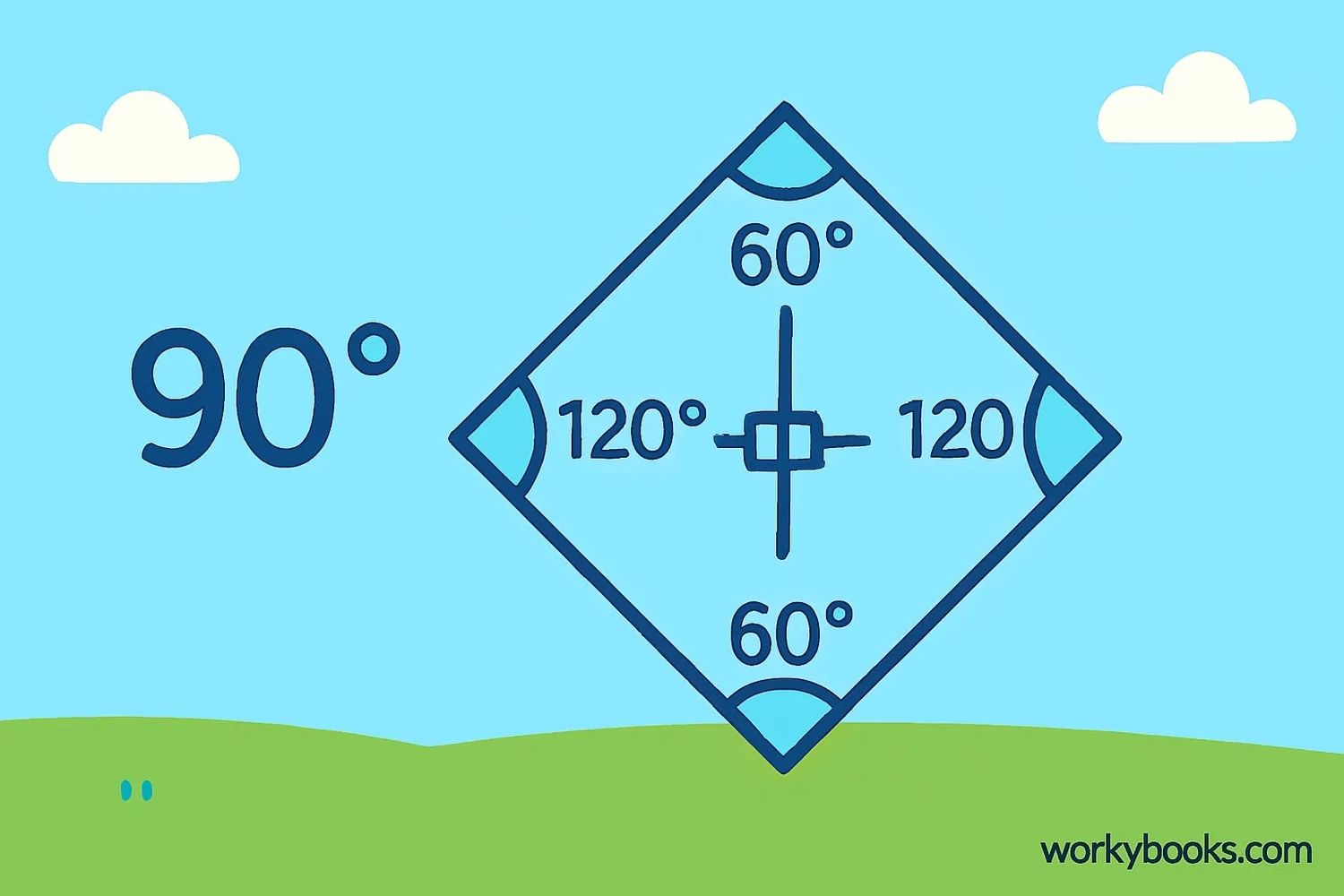
Rhombuses have some special properties that make them unique:
- All sides are equal: Each side has the same length
- Opposite sides are parallel: Just like in a parallelogram
- Opposite angles are equal: The angles facing each other are the same size
- Diagonals bisect each other at 90°: The diagonals cross at the center and form right angles
- Diagonals bisect the vertex angles: They cut the angles at the corners exactly in half
Remember
The diagonals of a rhombus always cross at right angles (90°), and they cut each other exactly in half at the center point.
Rhombus Formulas
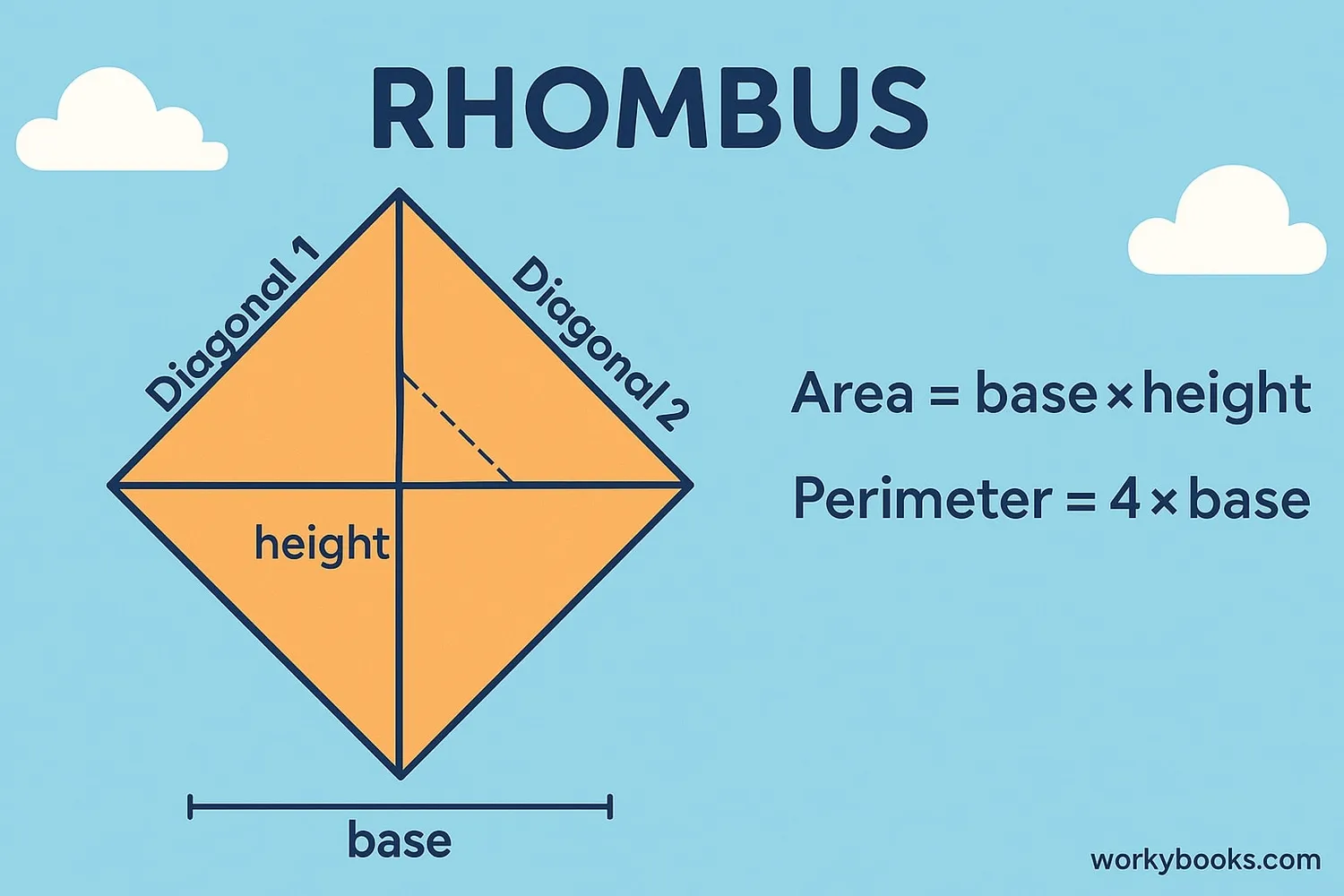
To work with rhombuses, we use two important formulas:
Area Formulas
Multiply the base length by the height (the perpendicular distance between sides)
Multiply the two diagonals and divide by two
Perimeter Formula
Since all sides are equal, multiply one side length by 4
Example: If a rhombus has sides of 5cm, what is its perimeter?
Perimeter = 4 × 5cm = 20cm
Example: If a rhombus has diagonals of 8cm and 6cm, what is its area?
Area = (8cm × 6cm) ÷ 2 = 48cm² ÷ 2 = 24cm²
Formula Tip
You can calculate the area using either method. Sometimes one is easier than the other depending on what measurements you have!
Rhombus vs Square
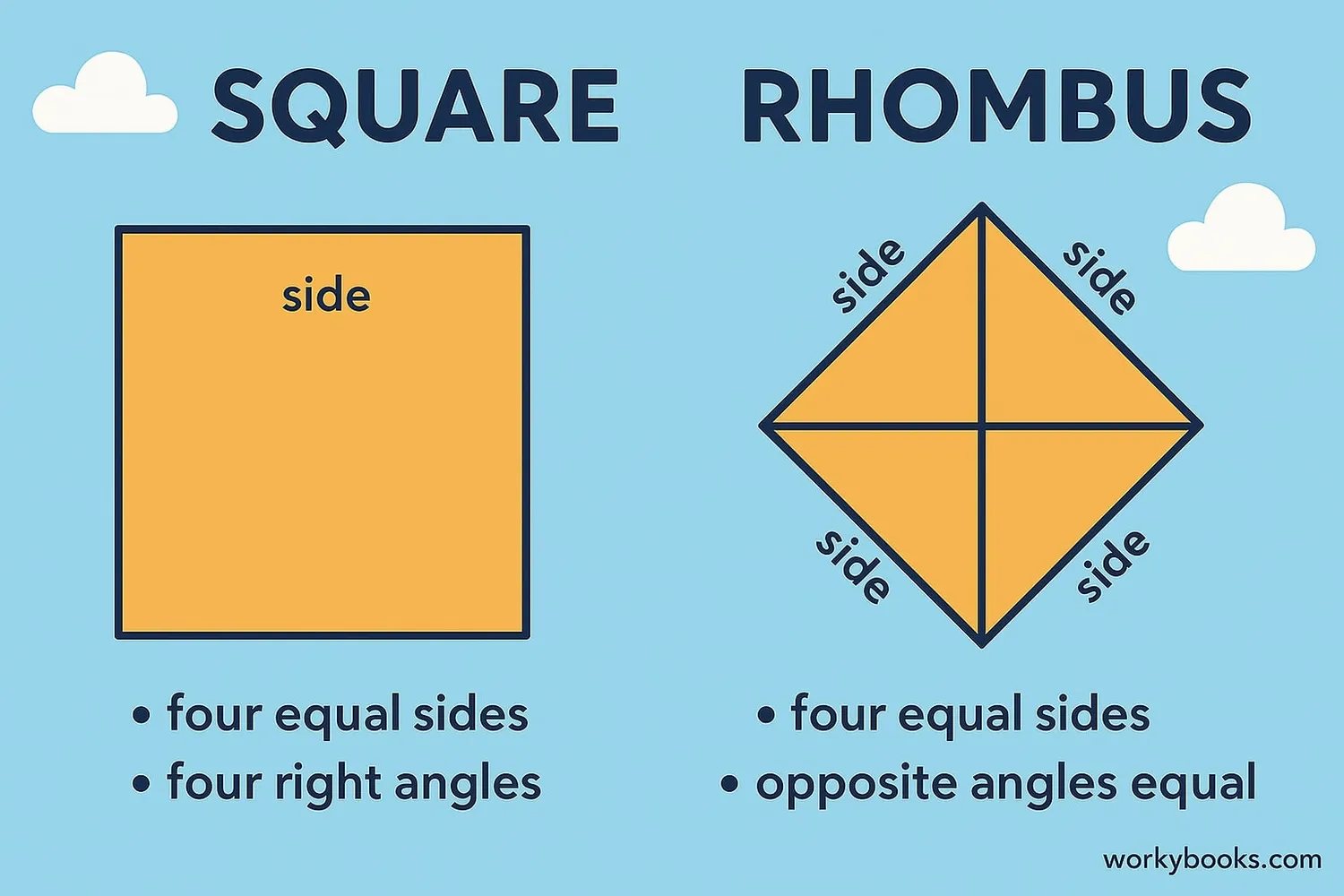
Rhombuses and squares are both special quadrilaterals, but they have important differences:
| Property | Rhombus | Square |
|---|---|---|
| All sides equal | ✓ | ✓ |
| Opposite sides parallel | ✓ | ✓ |
| All angles 90° | ✕ | ✓ |
| Diagonals equal length | ✕ | ✓ |
| Diagonals bisect at 90° | ✓ | ✓ |
Key difference: A square has all angles equal to 90 degrees, while a rhombus does not necessarily have right angles. A square is actually a special type of rhombus that has all right angles.
Think of it this way: All squares are rhombuses, but not all rhombuses are squares. It's like how all poodles are dogs, but not all dogs are poodles!
Remember
A square is a special rhombus with all right angles. Every square is a rhombus, but a rhombus isn't always a square.
Real-World Examples
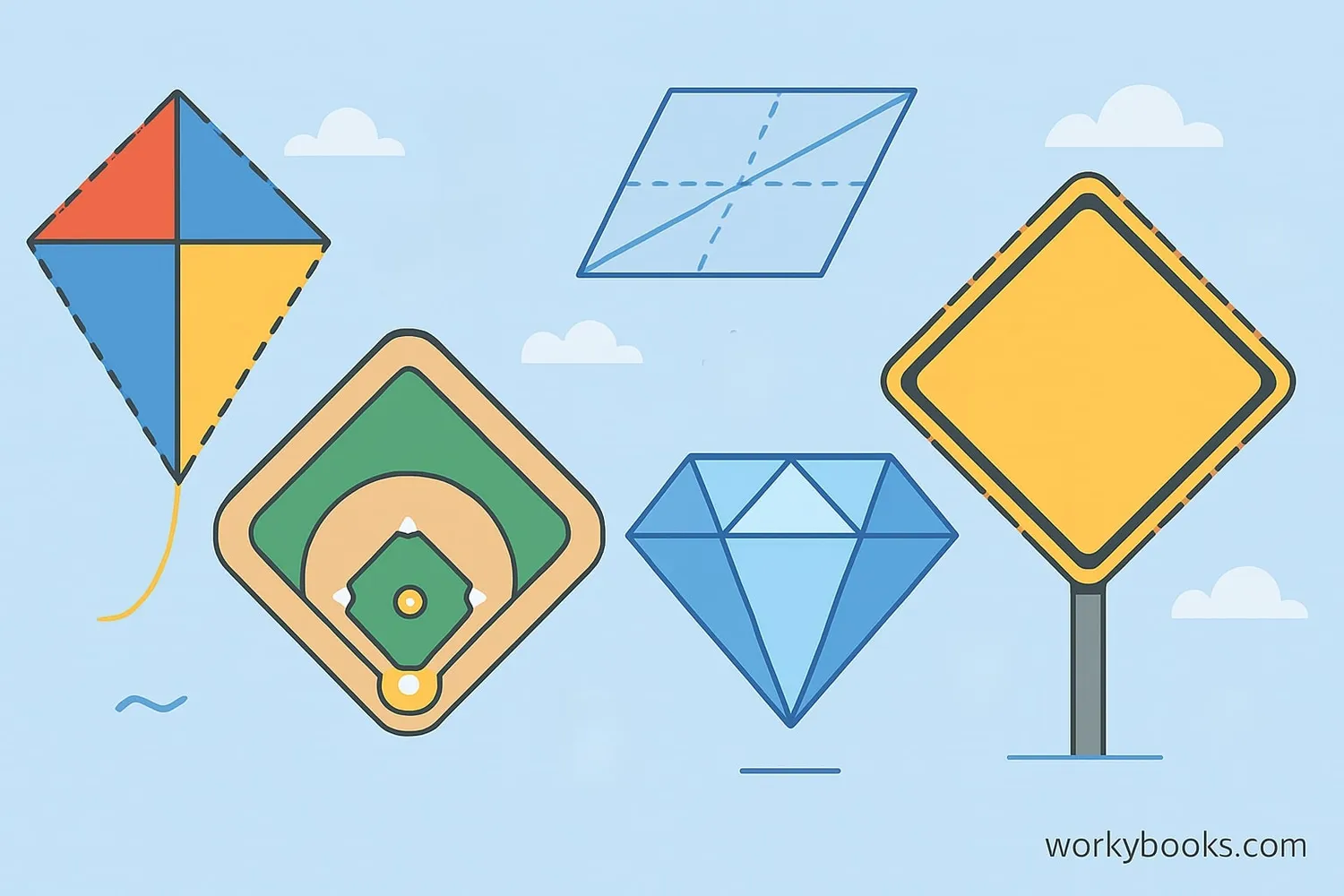
Rhombuses are all around us! Here are some common examples:
1. Kites: Many kites are shaped like rhombuses. The diamond-shaped kite is a classic example.
2. Baseball diamonds: The infield of a baseball field is actually a rhombus shape!
3. Playing cards: The diamond suit (♦) is shaped like a rhombus.
4. Road signs: Some warning signs use rhombus shapes to catch drivers' attention.
5. Tiles and patterns: Rhombus shapes are often used in floor tiles, quilts, and decorative patterns.
Next time you're outside, try to spot rhombus shapes in your environment. You might be surprised how many you find!
Activity
Look around your classroom or home. Can you find at least three objects that have rhombus shapes?
Rhombus Quiz
Test your knowledge about rhombuses with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about rhombuses:
Geometry Trivia
Discover interesting facts about rhombuses and geometry:
Ancient Use
Rhombus shapes have been used in art and architecture for thousands of years. Ancient Greek temples often used rhombus patterns in their mosaic floors.
Crystal Structures
In nature, many crystals form in rhombus shapes. The mineral calcite often breaks into perfect rhombus-shaped pieces called rhombohedrons.
3D Shapes
A 3D shape with rhombus faces is called a rhombohedron. This shape has six faces that are all identical rhombuses.
Tiling Patterns
Rhombus shapes can tile a plane without gaps or overlaps. This property makes them useful in quilting patterns and architectural designs.





