Rhombus vs Square - Definition, Examples, Quiz, FAQ, Trivia
Learn to identify these similar quadrilateral shapes with easy explanations and practice activities
What is a Quadrilateral?
A quadrilateral is a polygon with four sides and four angles. The word "quadrilateral" comes from Latin: "quadri" meaning four and "latus" meaning side.
Quadrilaterals come in many forms. Some have equal sides, some have right angles, and some have both! Today we'll focus on two special types: the rhombus and the square. Both are quadrilaterals with all four sides equal, but they have important differences that we'll explore.
All squares are rhombuses, but not all rhombuses are squares. This is because a square is a special type of rhombus that has right angles.
Key Concept
A rhombus is a quadrilateral with all four sides of equal length. A square is a special rhombus that also has four right angles.
Definitions: Rhombus and Square
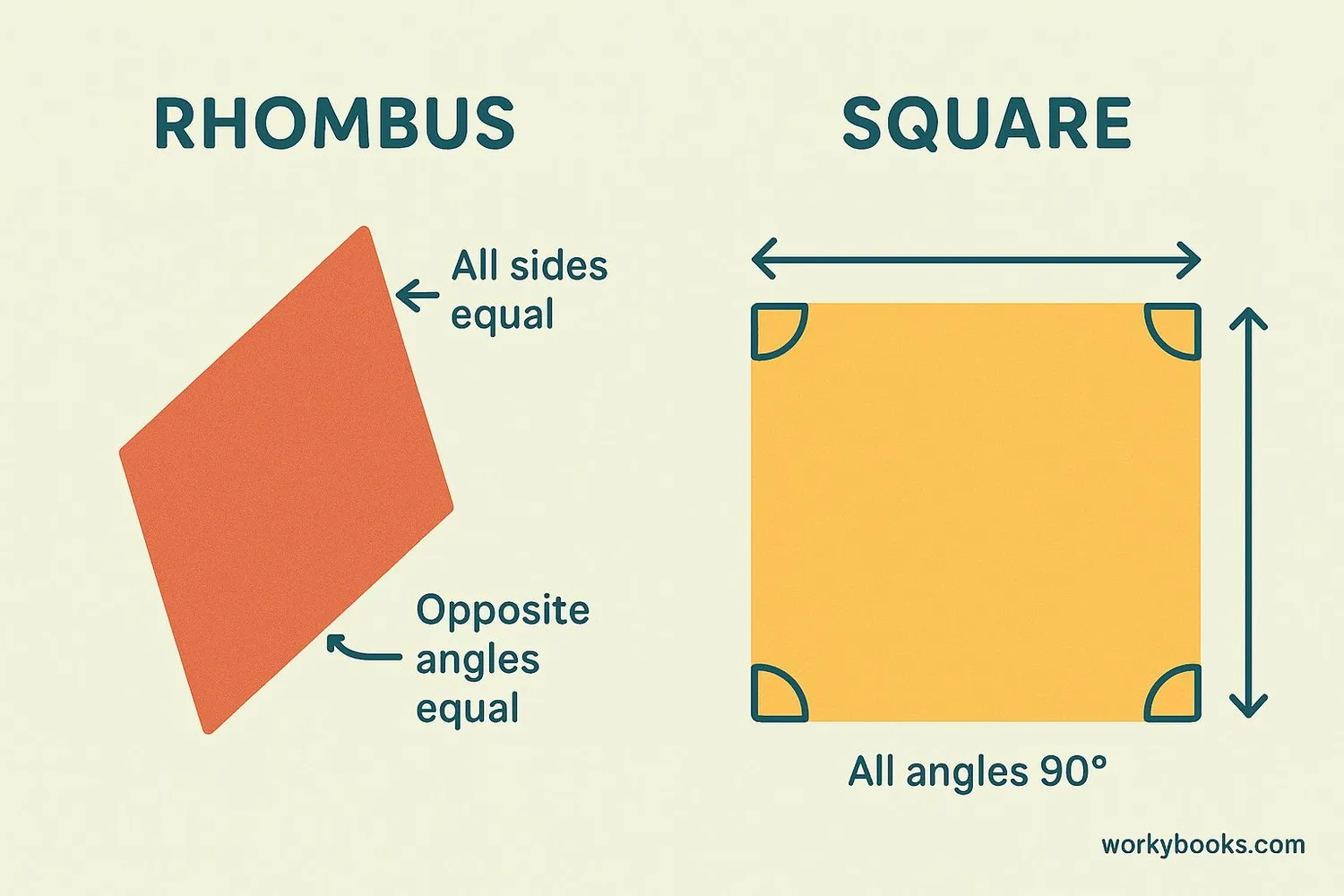
Let's break down these definitions:
Rhombus:
- All sides are equal in length
- Opposite sides are parallel
- Opposite angles are equal
- Diagonals bisect each other at right angles (90°)
- All sides are equal in length
- All angles are equal (90° each)
- Opposite sides are parallel
- Diagonals are equal in length and bisect each other at right angles
Remember
Every square is a rhombus because it has four equal sides, but not every rhombus is a square because rhombuses don't necessarily have right angles.
Properties Comparison
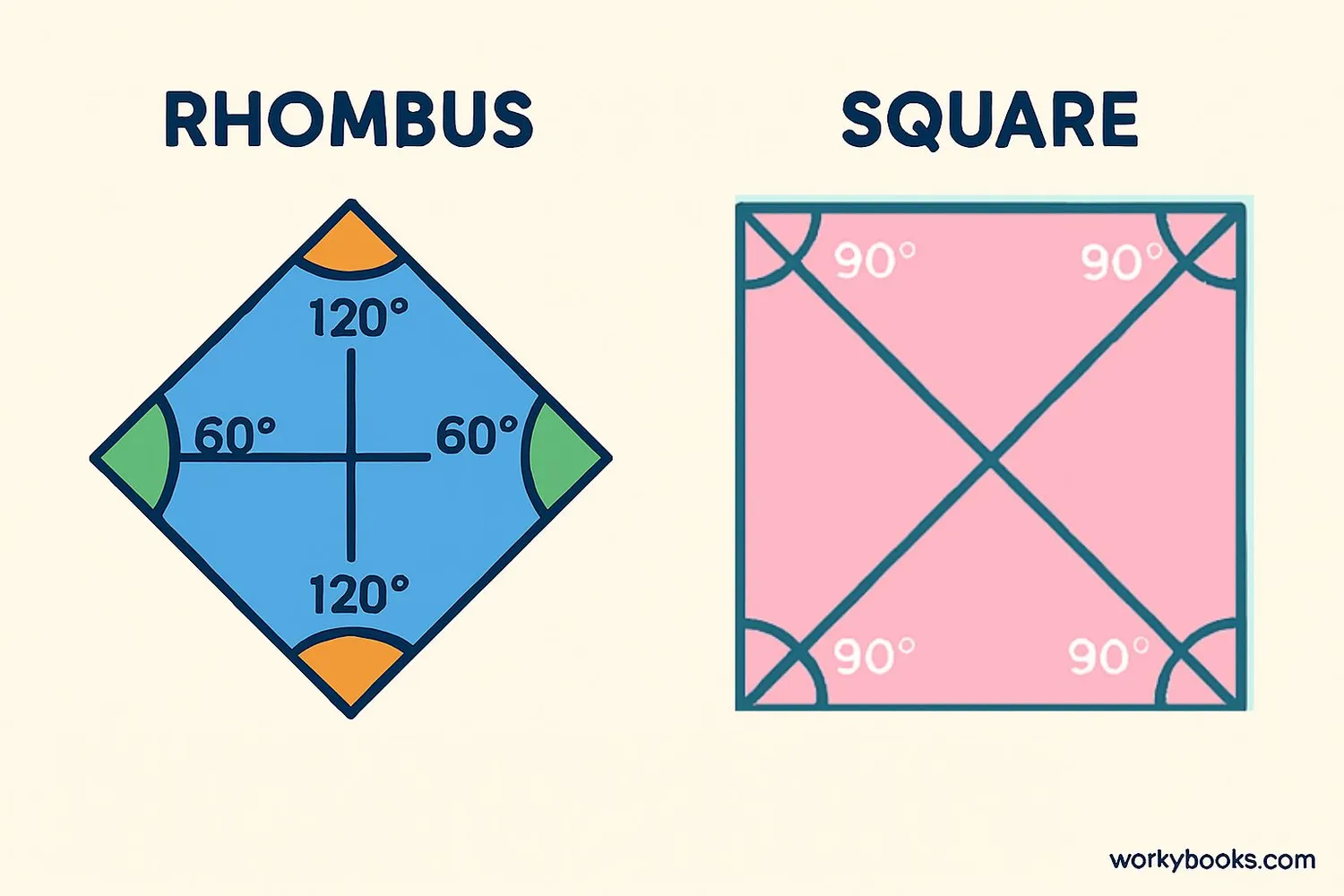
Let's compare the properties of rhombuses and squares in detail:
| Property | Rhombus | Square |
|---|---|---|
| Sides | All equal | All equal |
| Angles | Opposite equal, not necessarily 90° | All 90° |
| Diagonals | Unequal, bisect at 90° | Equal, bisect at 90° |
| Symmetry | 2-fold rotational symmetry | 4-fold rotational symmetry |
| Parallel sides | Two pairs | Two pairs |
| Relationship | Special parallelogram | Special rhombus and rectangle |
Important Note
The key difference is in the angles: a square has four right angles, while a rhombus has equal opposite angles that are not necessarily right angles.
Key Differences
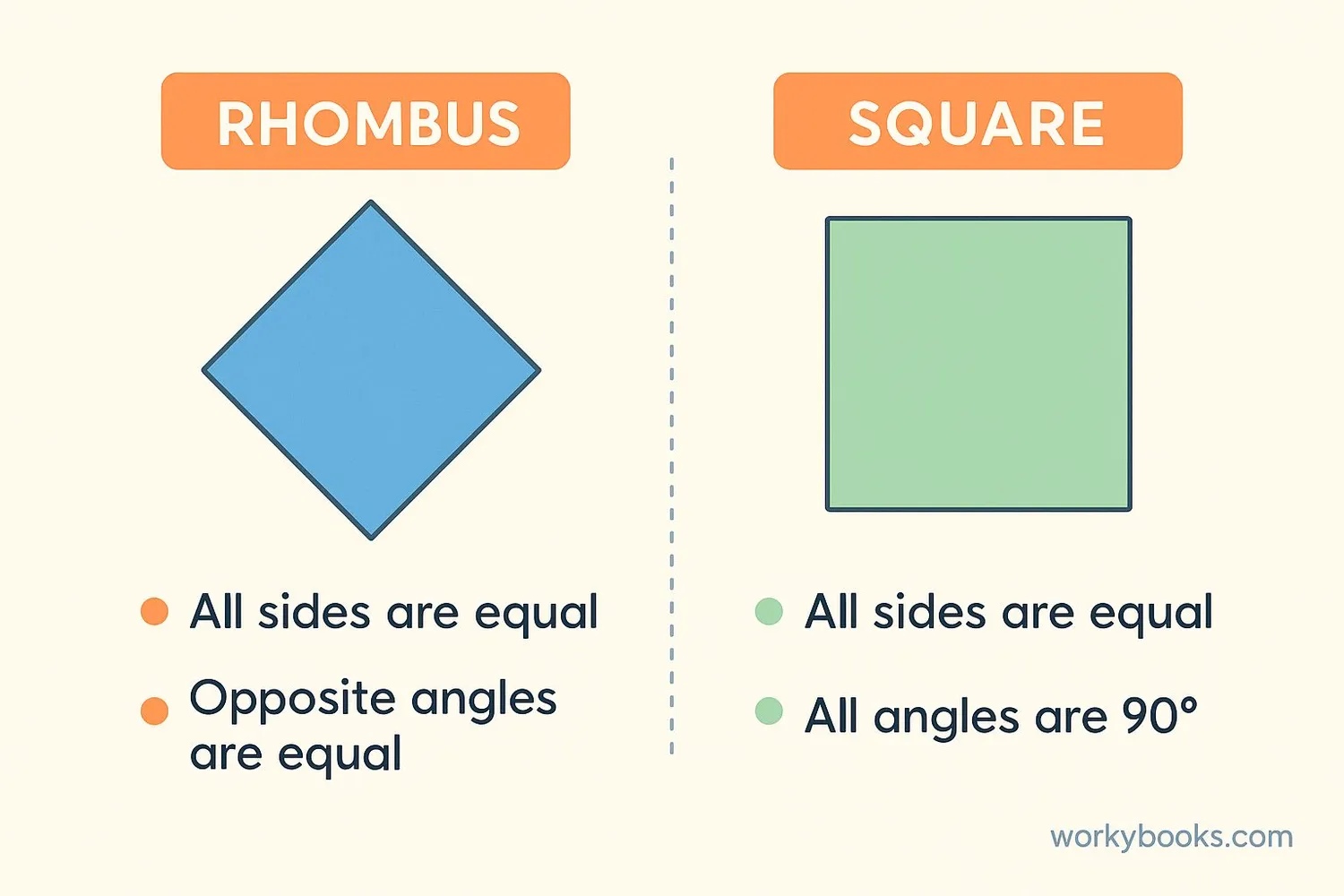
Here's a clear summary of the main differences between rhombuses and squares:
1. Angles:
- In a square, all angles are 90°
- In a rhombus, angles are not necessarily 90°
- In a square, diagonals are equal in length
- In a rhombus, diagonals are unequal
- All squares are rhombuses
- Not all rhombuses are squares
- A square has four lines of symmetry
- A rhombus has two lines of symmetry
- Square: Area = side × side
- Rhombus: Area = (diagonal1 × diagonal2) ÷ 2
Memory Tip
Think of a rhombus as a "leaning square." When you straighten a rhombus to make all angles 90°, it becomes a square!
Real-World Examples
Let's look at some real-world examples of rhombuses and squares:
Rhombus Examples:
- Baseball diamond: The infield is a rhombus shape with equal sides but no right angles
- Kites: Many traditional kites have a rhombus shape
- Road signs: Some warning signs are rhombus-shaped
- Tiles: Certain tile patterns use rhombus shapes
- Chessboard: The board is made of 64 small squares
- Windows: Many windows are square-shaped
- Post-it notes: These sticky notes are usually square
- Floor tiles: Many floor tiles are perfect squares
Activity Idea
Look around your classroom or home. How many rhombus and square shapes can you find? Try drawing them in your notebook!
Shape Identification Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about rhombuses and squares:
Geometry Trivia
Discover interesting facts about shapes and geometry:
Ancient Geometry
The word "rhombus" comes from the Greek word "rhombos," meaning something that spins. This refers to the shape's appearance that could resemble a spinning top.
Crystal Shapes
In nature, many crystals form rhombus shapes. For example, calcite crystals often break into perfect rhombuses when split along their natural cleavage planes.
Art and Design
Rhombus shapes are common in Islamic art and architecture, where they're used in intricate geometric patterns called "girih" that decorate mosques and palaces.
Mathematical Perfection
A square is the most symmetric quadrilateral, with four lines of symmetry and rotational symmetry of order 4 (it looks the same when rotated 90°, 180°, or 270°).





