Right Angle - Definition, Examples, Quiz, FAQ, Trivia
Learn about 90-degree angles, right triangles, and the Pythagorean theorem with visual examples and practice activities
What is a Right Angle?

A right angle is an angle that measures exactly 90 degrees. It looks like the corner of a square or rectangle. When two straight lines meet at a right angle, we say they are perpendicular to each other.
Right angles are everywhere around us:
- Corners of books and notebooks
- Edges of doors and windows
- Intersections of streets
- Corners of tables and desks
The special symbol for a right angle is a small square drawn in the corner where the two lines meet. This helps us recognize right angles in diagrams and drawings.
Key Concept
A right angle always measures exactly 90 degrees and is represented by a square symbol in diagrams.
Right Angle Triangle
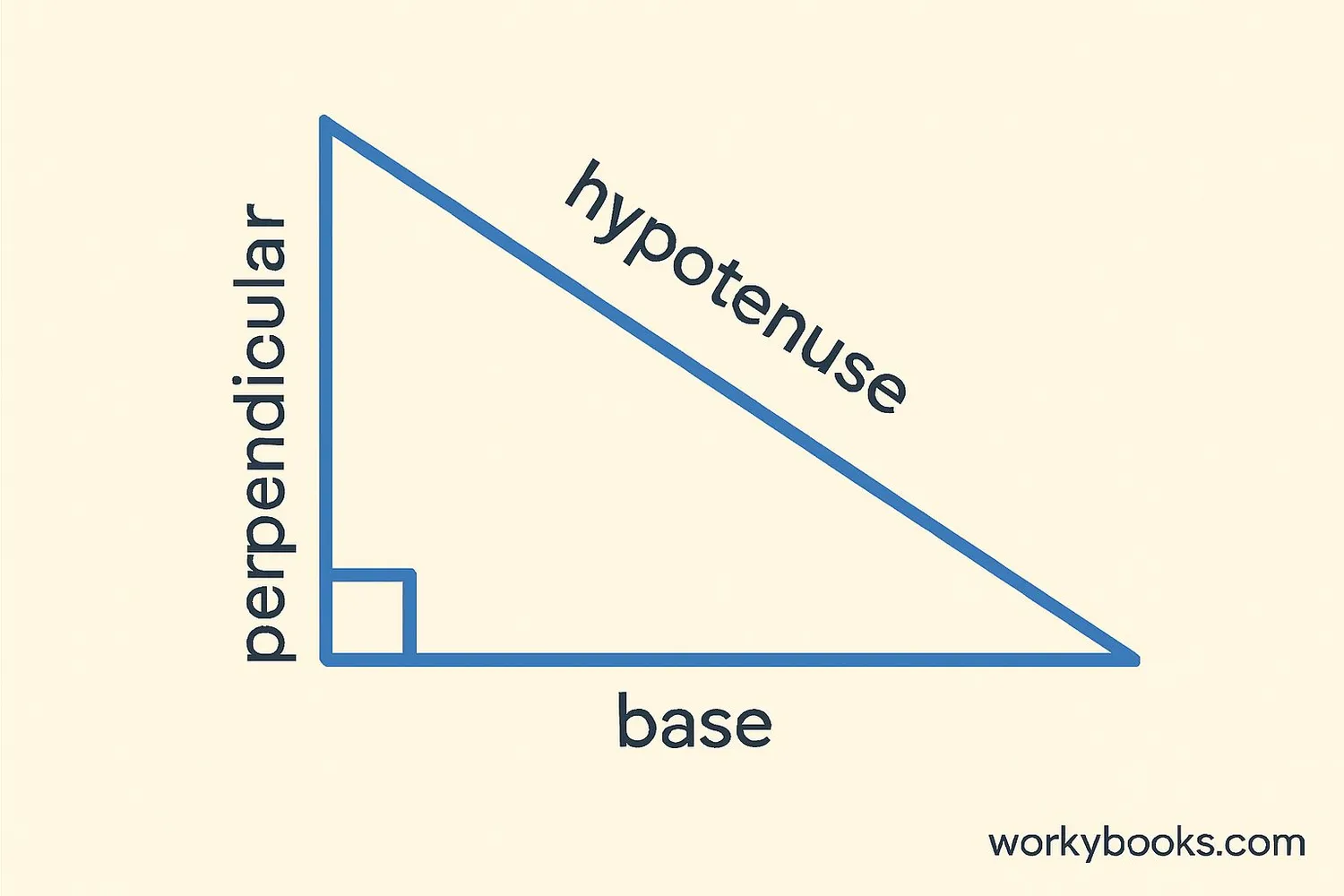
A right angle triangle (or right-angled triangle) is a triangle that has one angle measuring exactly 90 degrees. The side opposite the right angle is called the hypotenuse, and it's always the longest side of the triangle. The other two sides are called the perpendicular (or height) and the base.
Area of a Right Triangle
To find the area, multiply the base by the height and then divide by 2.
Area = ½ × 6 cm × 4 cm = 12 cm²
Right triangles are special because they follow the Pythagorean theorem, which helps us find missing side lengths.
Remember
In a right triangle, the hypotenuse is always opposite the right angle and is the longest side.
Pythagorean Theorem
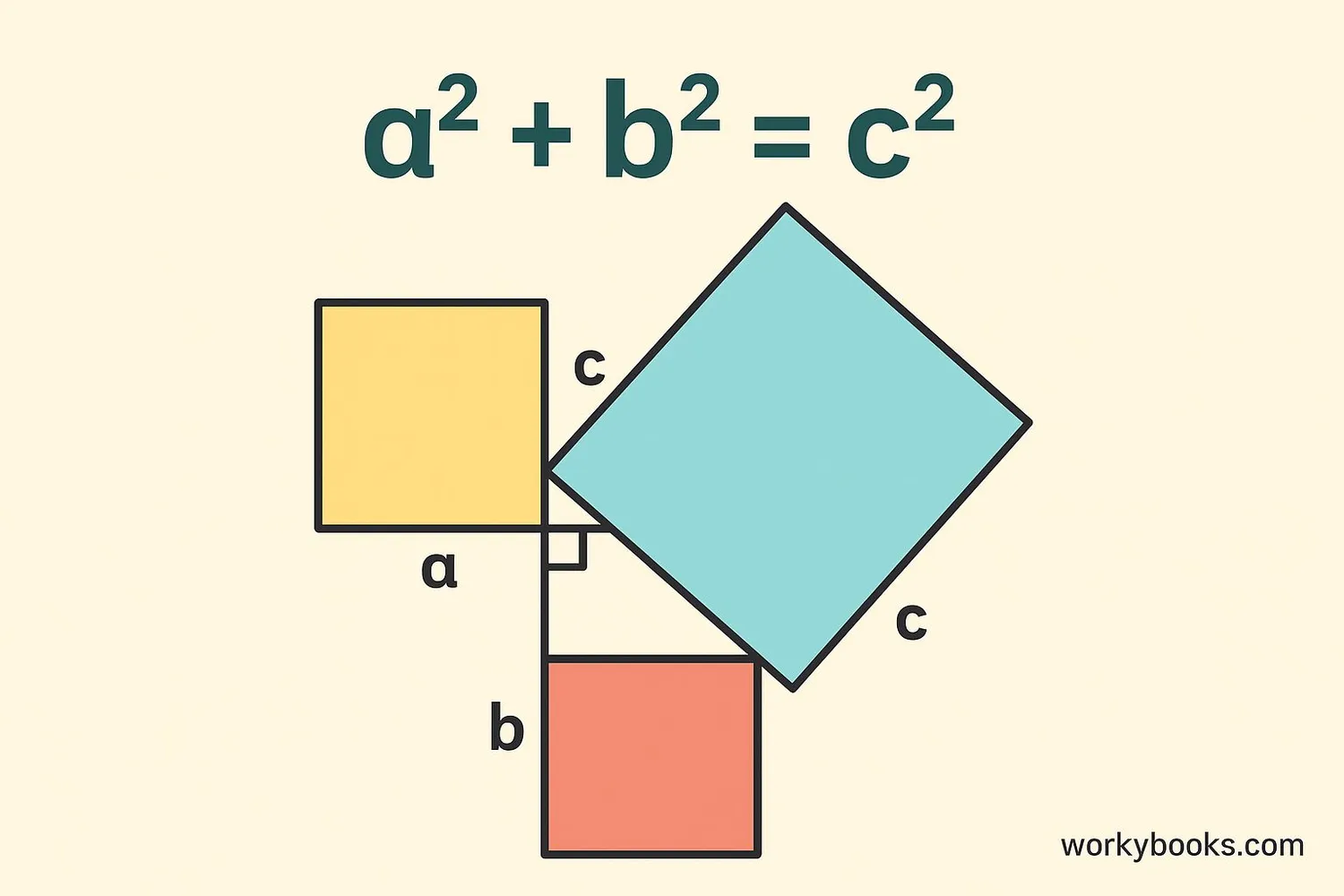
The Pythagorean theorem is a special rule that only works for right triangles. It states that:
Pythagorean Theorem
Where 'c' is the hypotenuse, and 'a' and 'b' are the other two sides.
Example: If a right triangle has sides of 3 cm and 4 cm:
3² + 4² = 9 + 16 = 25
The hypotenuse would be √25 = 5 cm
This theorem is useful for finding distances, constructing right angles, and solving many geometry problems.
Math Tip
The Pythagorean theorem only works for right triangles. For other triangles, you'll need different rules.
Real-World Examples

Right angles and right triangles appear in many real-world situations:
Example 1: When a ladder leans against a wall, it forms a right triangle with the wall and the ground. The ladder is the hypotenuse.
Example 2: The corners of rooms, doors, and windows are usually right angles. Builders use special tools to make sure these angles are exactly 90 degrees.
Example 3: In navigation, the Pythagorean theorem helps calculate the shortest distance between two points. If you walk 3 blocks east and then 4 blocks north, you've actually traveled 5 blocks from your starting point (as the crow flies).
Example 4: TV and computer screens are measured diagonally (the hypotenuse) but their width and height form a right angle.
Look around you - how many right angles can you spot in your classroom or home?
Activity Idea
Use a protractor to measure angles in your classroom. Count how many are exactly 90 degrees!
Right Angle Quiz
Test your knowledge with this 5-question quiz about right angles and triangles.
Frequently Asked Questions
Here are answers to common questions about right angles:
Geometry Trivia
Discover interesting facts about right angles and geometry:
Ancient Right Angles
The ancient Egyptians used right angles extensively in building the pyramids. They created perfect right angles by tying 12 equally spaced knots in a rope and forming a 3-4-5 triangle (3² + 4² = 5²).
Right Angles in Nature
While right angles are common in human-made objects, they're rare in nature. Some crystals form right angles, and honeycomb cells have angles close to 120 degrees, not 90.
Right Angles in Space
Astronauts use right angles to navigate in space. The International Space Station's solar panels are arranged at right angles to maximize sunlight exposure as the station orbits Earth.
Largest Right Angle
The Great Pyramid of Giza has corners that form nearly perfect right angles. Despite being built over 4,500 years ago, the average deviation from a perfect 90-degree angle is less than 0.05 degrees!





