Simplify Fraction - Definition, Examples, Quiz, FAQ, Trivia
Learn to simplify fractions with easy explanations, visual examples, and interactive practice
What is Simplifying Fractions?
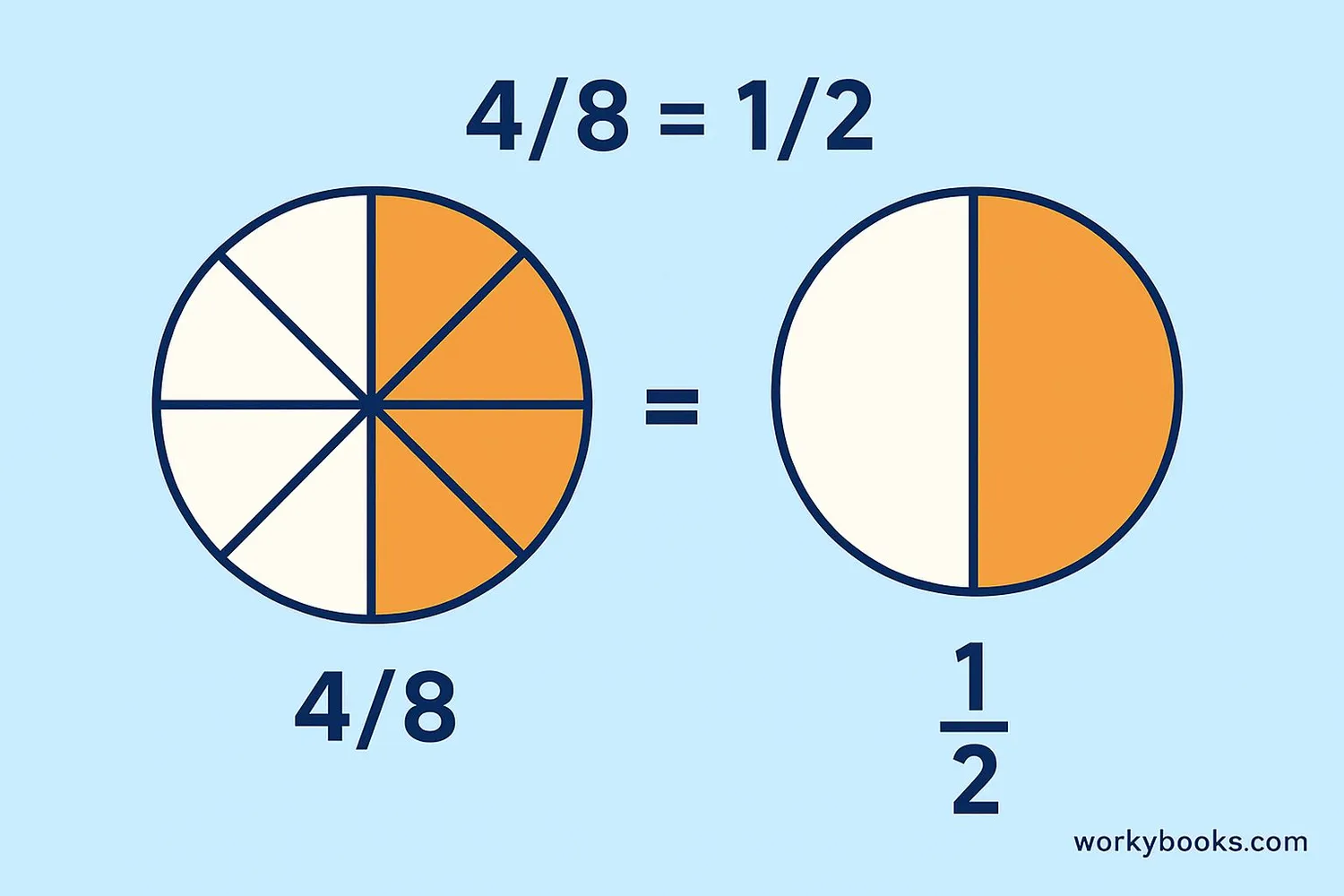
Simplifying fractions means making them as simple as possible. It's like reducing a fraction to its smallest form without changing its value. When we simplify a fraction, we divide both the numerator (top number) and denominator (bottom number) by the same number until we can't divide anymore.
Why do we simplify? Smaller fractions are easier to work with! Imagine trying to compare 12/16 and 3/4. When we simplify 12/16 to 3/4, we can easily see they're the same. Simplifying helps us solve math problems faster and understand fractions better.
A fraction is in its simplest form when the only common factor between the numerator and denominator is 1. That means there's no number (other than 1) that divides evenly into both numbers.
Key Concept
Simplifying fractions doesn't change the value! 4/8 is the same as 1/2, just like two quarters are the same as one half-dollar.
How to Simplify Fractions

There are two main ways to simplify fractions. Let's learn both methods:
Method 1: Step-by-Step Division
- Find a number that divides evenly into both the numerator and denominator
- Divide both top and bottom by that number
- Repeat until you can't divide anymore
Divide by 2: 8÷2=4, 12÷2=6 → 4/6
Divide by 2 again: 4÷2=2, 6÷2=3 → 2/3
Method 2: Greatest Common Factor (GCF)
- Find the GCF of numerator and denominator
- Divide both by the GCF
- You have the simplified fraction!
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
GCF is 12 → 24÷12=2, 36÷12=3 → 2/3
Remember
Always check if your fraction can be simplified! Fractions with even numbers can usually be divided by 2. Fractions ending with 0 or 5 can usually be divided by 5.
Simplification Examples
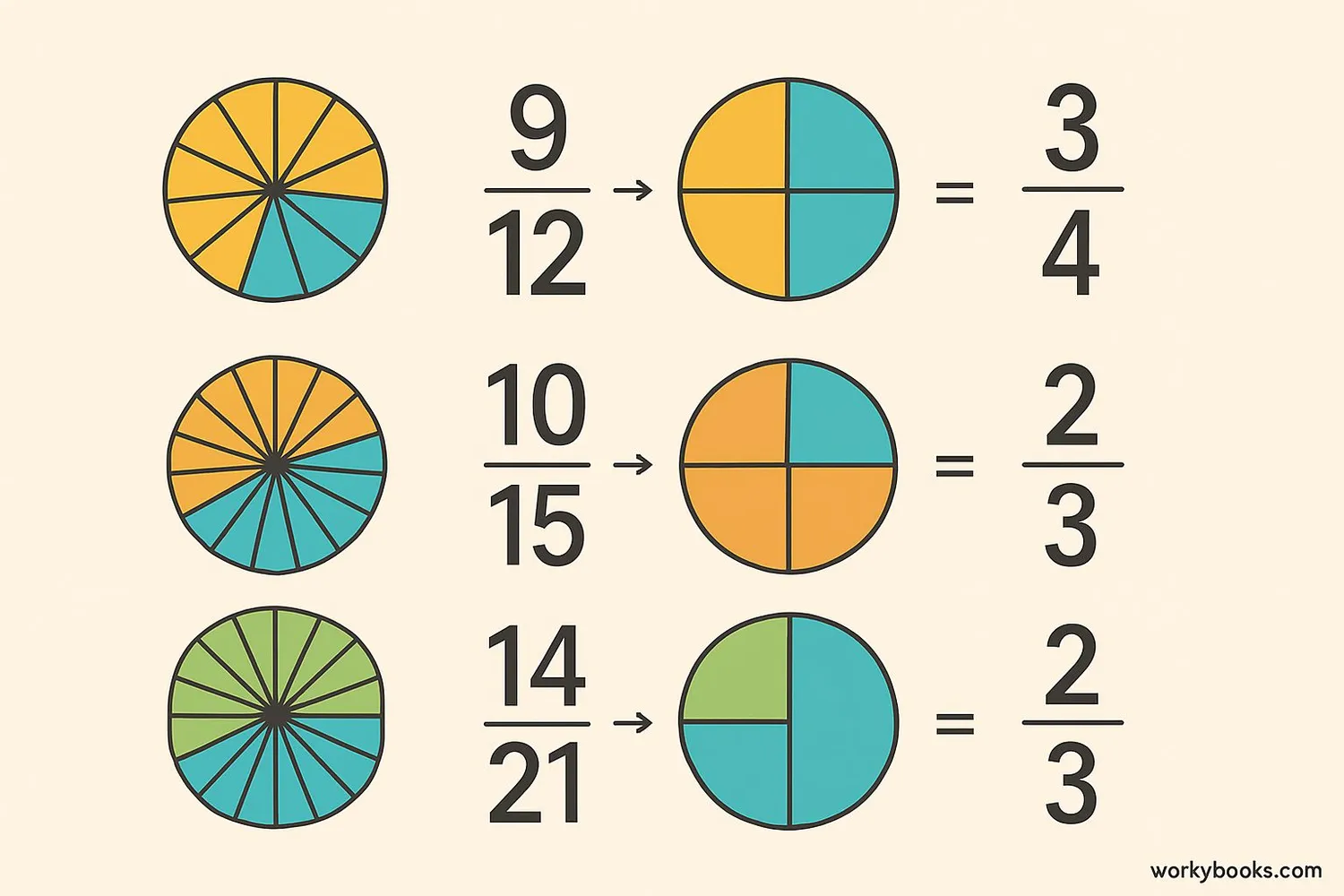
Example 1: 6/8
Step 1: Find factors: 6 (1,2,3,6) and 8 (1,2,4,8)
Step 2: Common factors: 1 and 2
Step 3: GCF is 2
Step 4: 6÷2=3, 8÷2=4
Simplified:
Example 2: 15/25
Step 1: Both divisible by 5
Step 2: 15÷5=3, 25÷5=5
Simplified:
Example 3: 9/27
Step 1: Factors: 9 (1,3,9) and 27 (1,3,9,27)
Step 2: GCF is 9
Step 3: 9÷9=1, 27÷9=3
Simplified:
Simplification Tip
When you see large numbers, try dividing by small prime numbers first (2, 3, 5, 7). Keep dividing until you can't divide anymore!
Simplification Practice Quiz
Test your fraction simplification skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about simplifying fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC! But they only used unit fractions (with numerator 1) like 1/2, 1/3, 1/4. They would write 3/4 as 1/2 + 1/4.
Fractions in Nature
Fractions appear everywhere in nature! Bees make honeycombs with hexagonal cells that are perfect fractions of the whole structure. Sunflower seeds grow in spiral patterns following fractional sequences.
Fractions in Music
Musical rhythms are based on fractions! A whole note gets 4 beats, a half note gets 2 beats, a quarter note gets 1 beat. Musicians use fractions to read and play music accurately.
Largest Fraction
The fraction with the largest denominator ever used in a serious mathematical proof has a denominator of 10 to the power of 10 to the power of 10 to the power of 34! That's a 1 followed by more zeros than atoms in the universe!





