Skew Lines - Definition, Examples, Quiz, FAQ, Trivia
Discover how lines behave in 3D space with simple explanations and visual examples
What are Skew Lines?
Skew lines are lines that exist in three-dimensional space. They have two special properties:
1. They never intersect (they don't cross each other)
2. They are not parallel (they don't go in the same direction)
Imagine two straight roads going over and under a bridge. They never meet, but they're not going in the same direction either. That's like skew lines!
Skew lines only exist in 3D space. In 2D (like on paper), lines either intersect or are parallel. But when we add the third dimension (up/down), we get this special relationship.
Key Concept
Skew lines are non-coplanar, non-intersecting, and non-parallel lines in 3D space.
Properties of Skew Lines
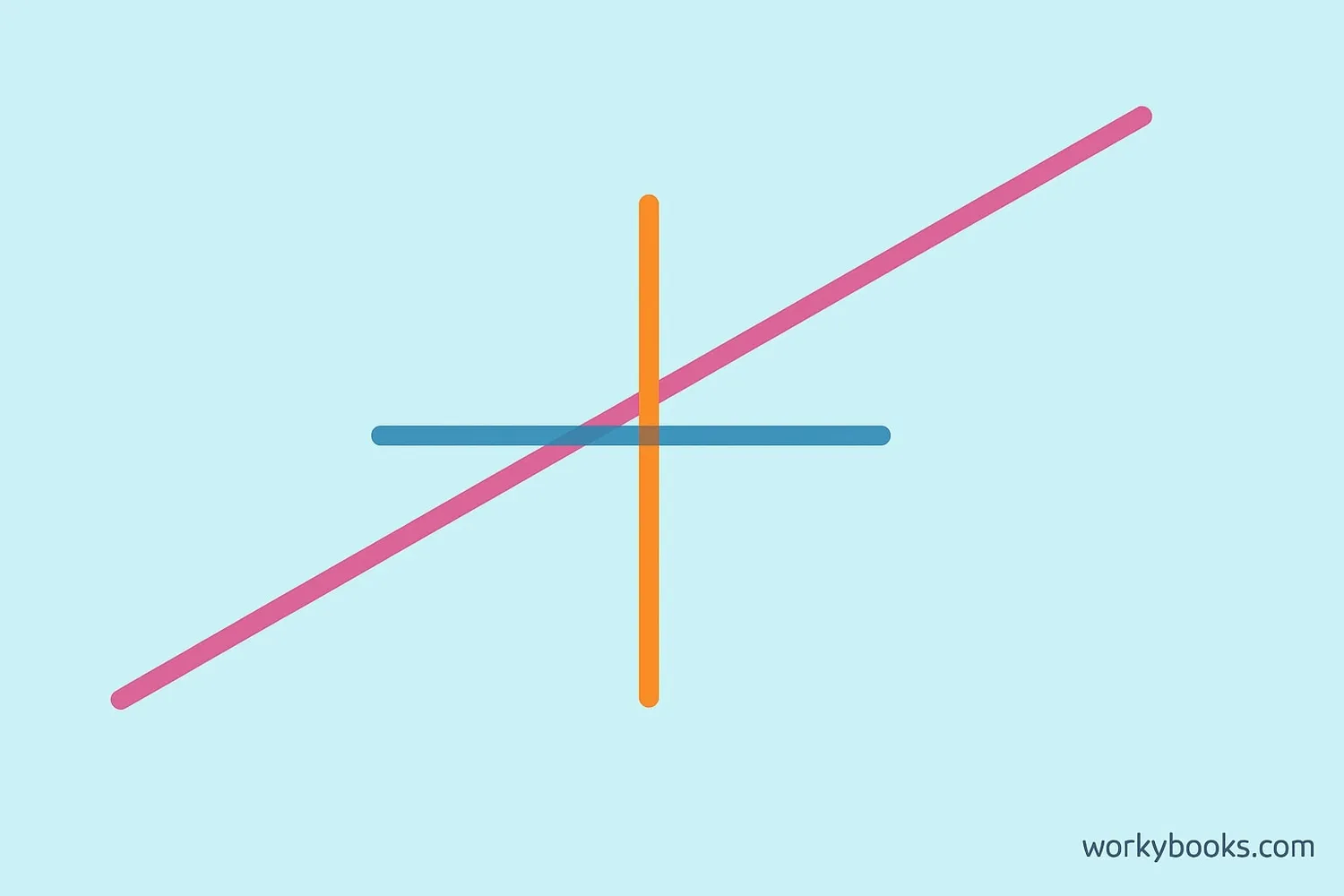
Skew lines have some interesting properties:
1. Never meet: No matter how far you extend them, they'll never touch.
2. Different directions: They're not going the same way (not parallel).
3. Shortest distance: There's always a shortest path between them, which is perpendicular to both lines.
4. Not in the same plane: You can't draw a flat surface that contains both lines.
The shortest distance between two skew lines is always measured along a line that's perpendicular to both. This distance is the smallest possible space between them.
Remember
Skew lines don't have to be at right angles to each other - they just need to not be parallel and not intersect.
Skew Lines in a Cube
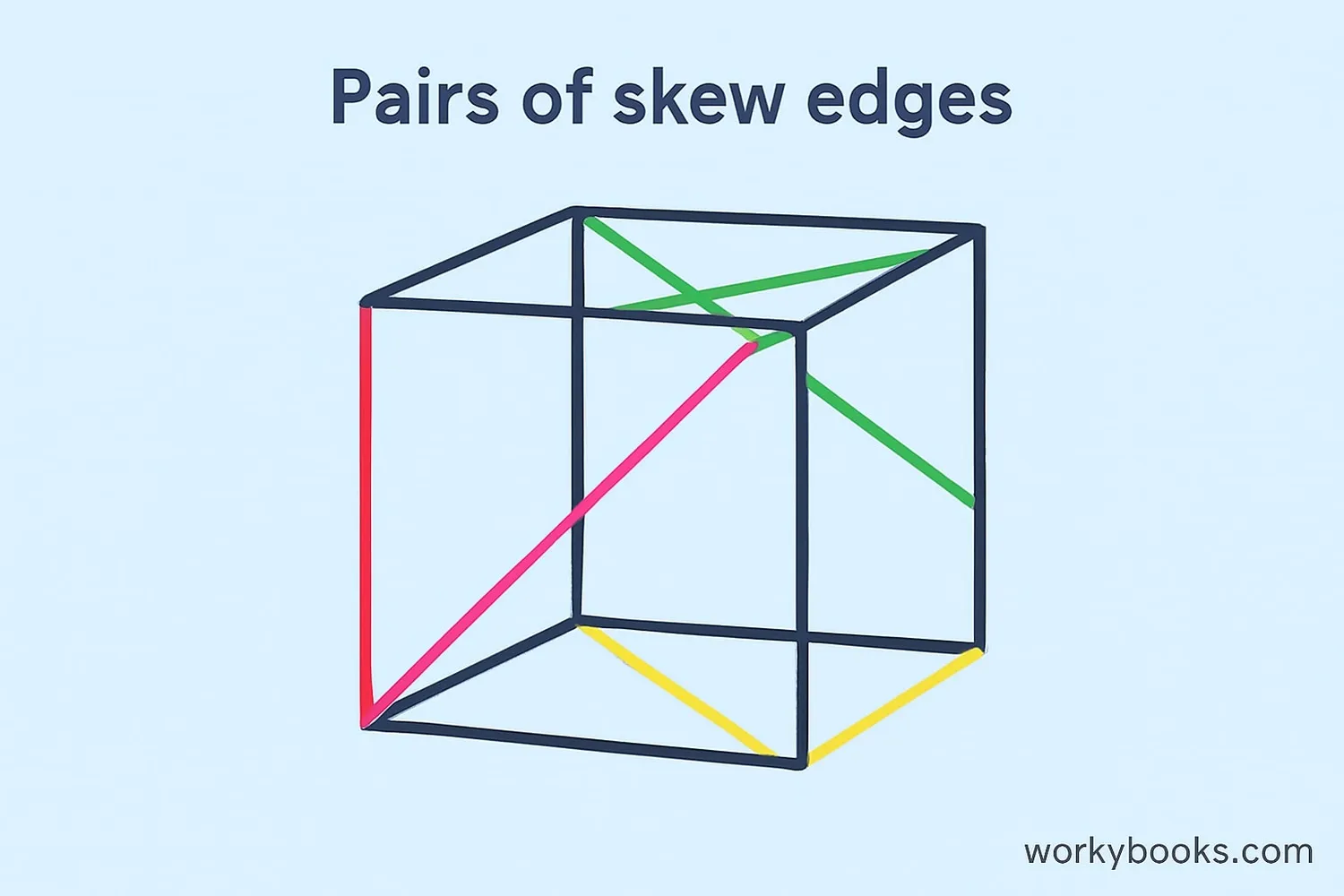
A cube is a great place to find skew lines! Look at these examples:
Example 1: Take one edge on the front face and another edge on the back face that's not directly behind it. These two edges are skew lines.
Example 2: An edge on the top face and an edge on the bottom face that aren't directly above/below each other are also skew lines.
In a cube, you'll find many pairs of skew lines. They help give the cube its 3D shape. Remember:
- Lines on the same face are either parallel or intersecting
- Lines on opposite faces might be parallel or skew
- Lines on adjacent faces might be intersecting or skew
Cube Tip
In a cube, two edges are skew if they are on different faces and don't meet at a corner.
Skew Lines vs Parallel Lines
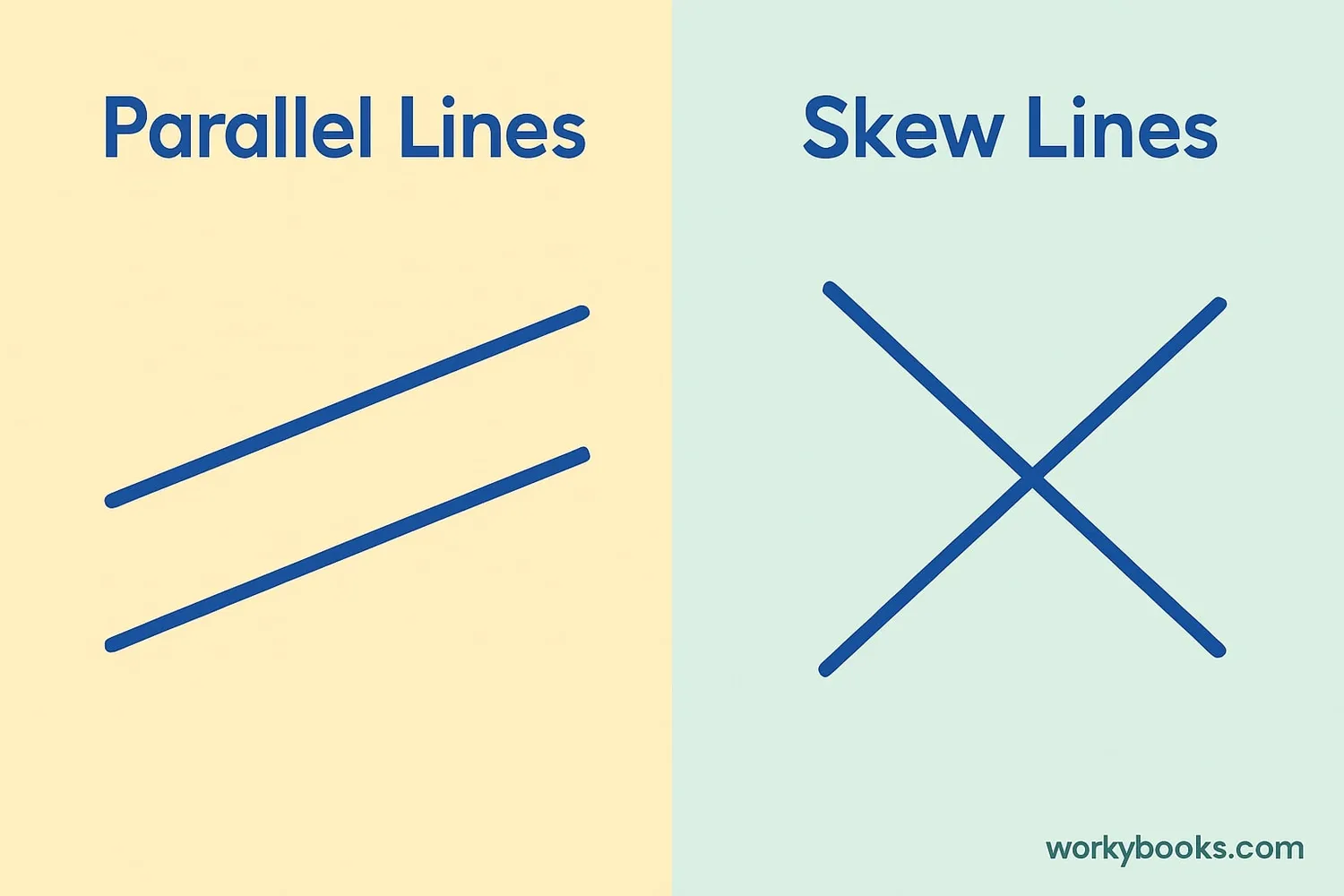
It's important to understand the difference between skew lines and parallel lines:
| Property | Skew Lines | Parallel Lines |
|---|---|---|
| Do they intersect? | Never | Never |
| Are they parallel? | No | Yes |
| Same direction? | No | Yes |
| Can they be in the same plane? | No | Yes |
| Distance between them | Changes along the line | Constant |
| Found in 2D space? | No | Yes |
The key difference is that parallel lines always go in exactly the same direction, while skew lines go in different directions. Both never meet, but for different reasons!
Comparison Tip
If two lines are not parallel and don't intersect in 3D space, they must be skew lines!
Skew Lines Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about skew lines:
Geometry Trivia
Discover interesting facts about geometry and skew lines:
Ancient Geometry
The concept of skew lines was first studied by ancient Greek mathematicians over 2,000 years ago. Euclid, known as the "Father of Geometry," wrote about spatial relationships.
In Engineering
Engineers use the concept of skew lines when designing bridges, roads, and overpasses that cross without intersecting at the same level.
In Chemistry
In molecular structures, the arrangement of atoms often creates skew lines between chemical bonds in 3D space.
Infinite Possibilities
In 3D space, there are infinitely many pairs of skew lines. They can be at any angle to each other as long as they don't intersect and aren't parallel.


