Square Root - Definition, Examples, Quiz, FAQ, Trivia
Learn what square roots are, how to calculate them, and practice with fun activities
What is a Square Root?

A square root of a number is a value that, when multiplied by itself, gives the original number. It's the opposite of squaring a number.
The square root symbol is called the radical symbol (√). The number inside the radical is called the radicand.
For example:
- √4 = 2 because 2 × 2 = 4
- √9 = 3 because 3 × 3 = 9
- √16 = 4 because 4 × 4 = 16
Square Root Formula
Where 'b' is the radicand and 'a' is the square root
Key Concept
The square root of a number answers the question: "What number multiplied by itself equals this number?"
Perfect Squares

Perfect squares are numbers that are the squares of whole numbers. They're called "perfect" because their square roots are whole numbers.
Here are the first 12 perfect squares:
Numbers that aren't perfect squares are called imperfect squares. Their square roots are not whole numbers and often have decimal parts that go on forever without repeating. For example:
√2 ≈ 1.414
√3 ≈ 1.732
√5 ≈ 2.236
Remember
Memorizing perfect squares up to 144 (12×12) will help you recognize square roots quickly!
Methods for Finding Square Roots
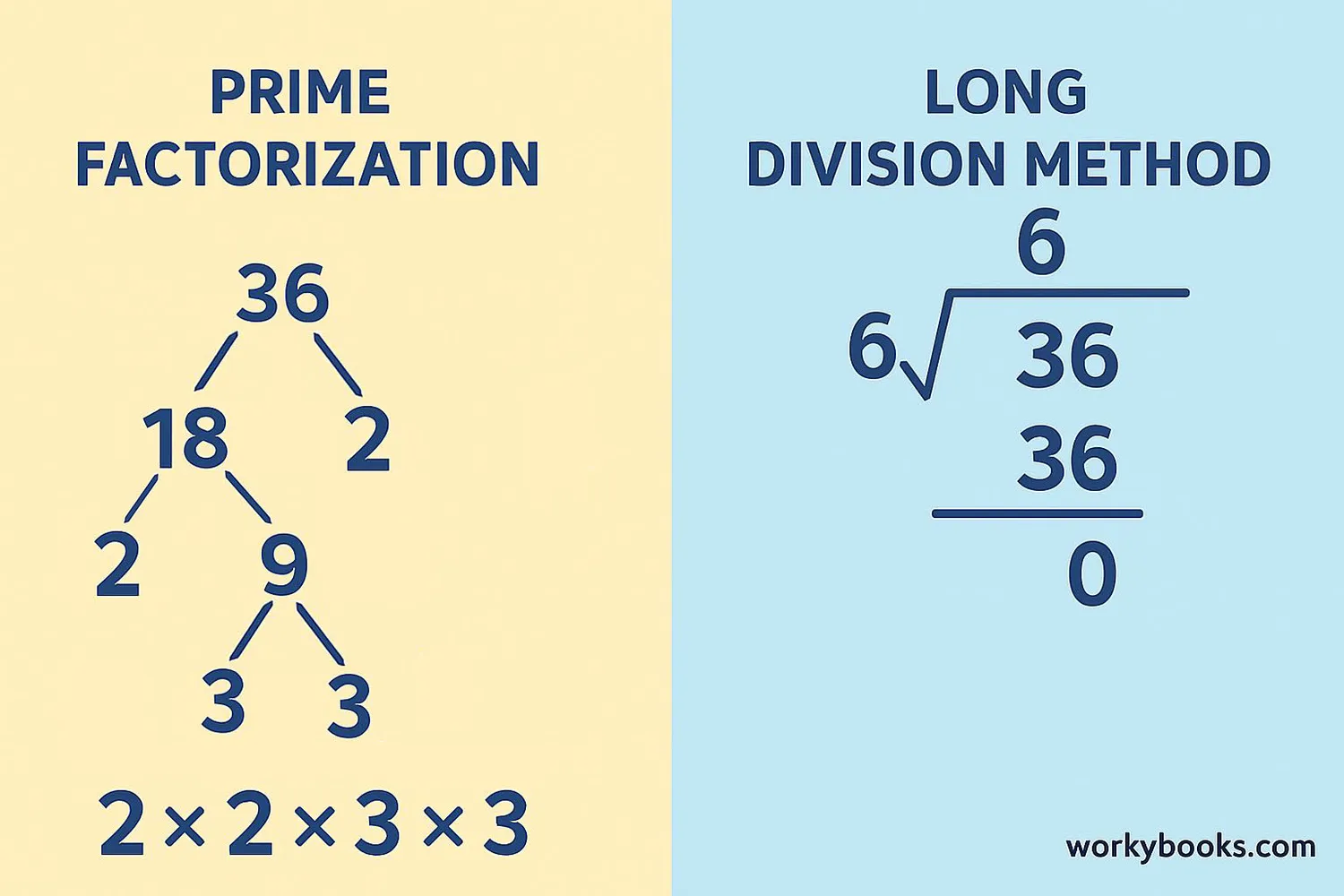
1. Prime Factorization Method
This method works well for perfect squares. Follow these steps:
Example: Find √36
Step 1: Prime factors: 36 = 2 × 2 × 3 × 3
Step 2: Group into pairs: (2×2) and (3×3)
Step 3: Take one from each pair: 2 and 3
Step 4: Multiply: 2 × 3 = 6
Answer: √36 = 6
2. Long Division Method
This method works for any number, including imperfect squares:
Example: Find √2
Using long division, we get √2 ≈ 1.414
Tip
For imperfect squares, you can use a calculator to find approximate values. Most calculators have a √ button.
Real-World Examples
Square roots are used in many real-life situations:
Example 1: Area of a square
If a square room has an area of 25 m², what is the length of each wall?
Solution: √25 = 5 meters
Example 2: Pythagorean theorem
In a right triangle with legs 3cm and 4cm, what is the hypotenuse?
Solution: √(3² + 4²) = √(9 + 16) = √25 = 5cm
Example 3: Screen size
A computer screen has 1,920 pixels horizontally and 1,080 pixels vertically. What is the diagonal size in pixels?
Solution: √(1920² + 1080²) = √(3,686,400 + 1,166,400) = √4,852,800 ≈ 2203 pixels
Example 4: Physics calculations
The time it takes an object to fall from height h is t = √(2h/g). If h = 20m and g=10m/s², find t.
Solution: t = √(2×20/10) = √(40/10) = √4 = 2 seconds
Practical Tip
Square roots help us understand relationships in geometry, physics, and even art and nature!
Square Root Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Square Roots
The Babylonians developed a method for approximating square roots as early as 2000 BCE. Their method was similar to the modern long division method and could calculate √2 to six decimal places!
Irrational Numbers
The square root of 2 was the first known irrational number - a number that cannot be expressed as a simple fraction. This discovery shocked ancient Greek mathematicians who believed all numbers were rational.
Square Roots in Computers
Computer algorithms for calculating square roots are based on ancient methods. The "fast inverse square root" method was famously used in the Quake III video game to make lighting calculations faster.
Memory Feats
The world record for reciting the most digits of √2 is held by Rajveer Meena from India, who recited 70,000 digits in 2020. It took him over 10 hours!





