Square Root of 2 - Definition, Examples, Quiz, FAQ, Trivia
Learn about square roots with clear explanations, examples, and practice activities
What is a Square Root?
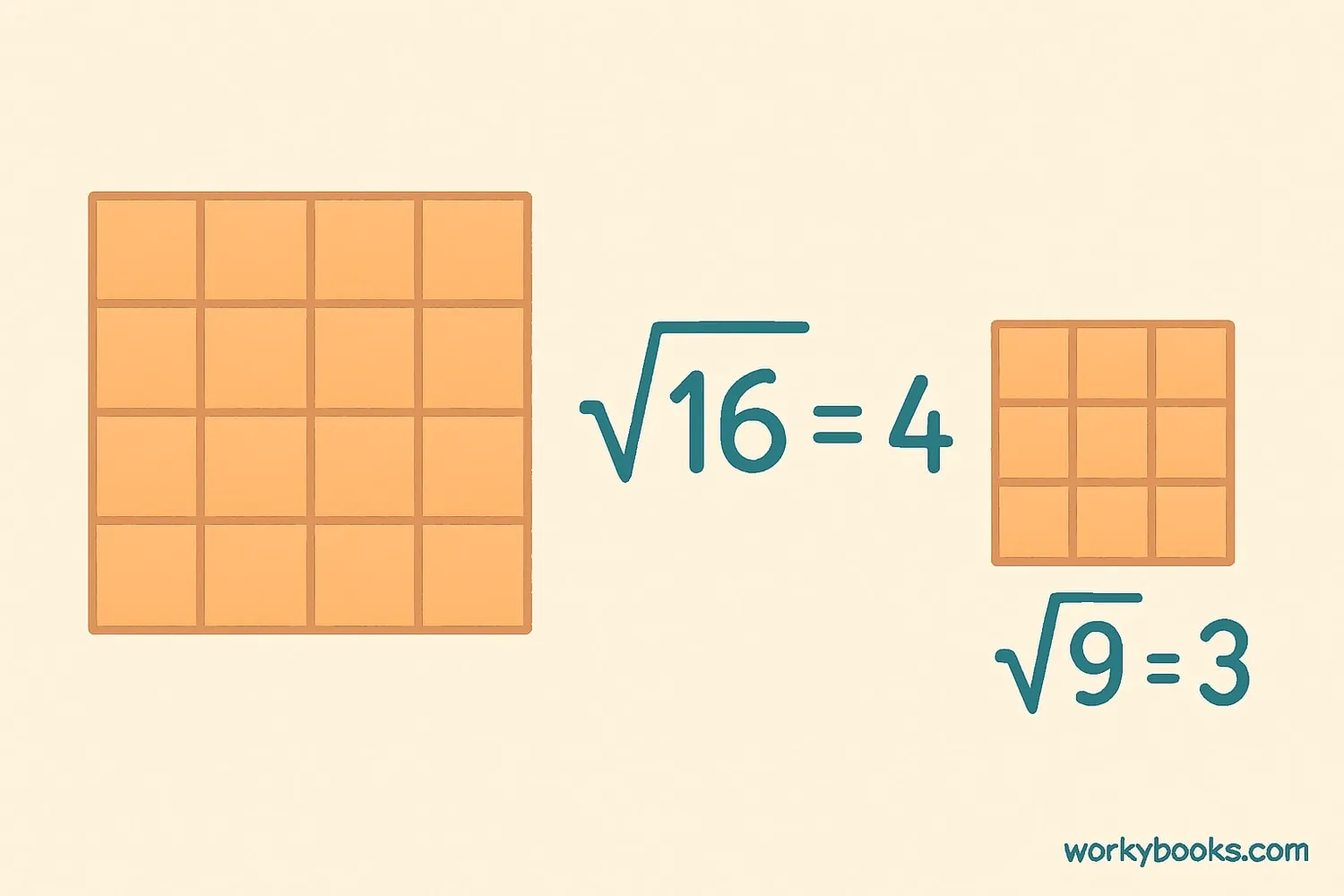
A square root is a special number that, when multiplied by itself, gives you the original number. Think of it as the opposite of squaring a number.
For example:
4 × 4 = 16, so the square root of 16 is 4. We write this as √16 = 4.
The symbol for square root is √, called the radical symbol. The number inside the radical symbol is called the radicand.
Numbers that have whole number square roots are called perfect squares. Examples include:
1 (√1 = 1), 4 (√4 = 2), 9 (√9 = 3), 16 (√16 = 4), and 25 (√25 = 5).
Square Root Definition
This means that the square root of a number is the value that can be multiplied by itself to give the original number.
Key Concept
Every positive number has two square roots: a positive root (called the principal square root) and a negative root.
The Square Root of 2
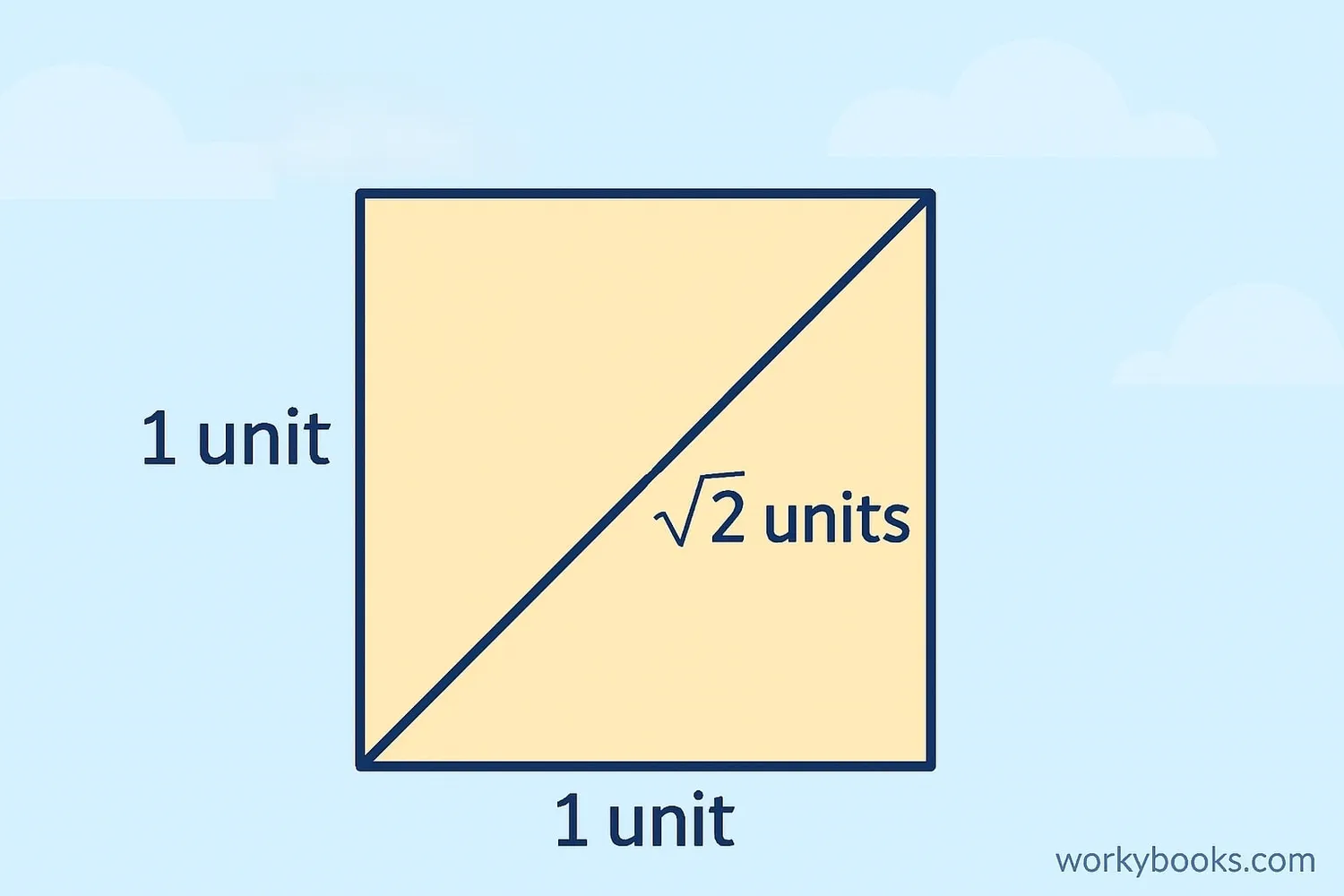
The square root of 2 (√2) is a special number because it's approximately 1.41421356237... but it goes on forever without repeating!
Why is √2 important? It appears in geometry when you calculate the diagonal of a square. For a square with sides of length 1:
√2 was one of the first numbers discovered to be irrational, meaning it cannot be written as a simple fraction of two whole numbers.
The decimal representation of √2 is approximately:
This decimal never ends and never repeats, which makes √2 an irrational number.
Remember
√2 is approximately 1.414. You can remember this as "I wish I knew the square root of two" (1.414 - one four one four).
Methods to Find √2
Since √2 is irrational, we can't find its exact value, but we can approximate it using different methods. Here are two common methods:
1. Prime Factorization Method
- Write 2 as a product of prime factors: 2 is already prime
- Group the factors in pairs: Since there's only one 2, we can't make a pair
- Since we can't pair all factors, √2 cannot be simplified to a whole number
- This shows that √2 is irrational
2. Long Division Method
- Place a bar over the number 2 to start the division
- Find the largest number whose square is less than or equal to 2 (1)
- Subtract 1² = 1 from 2, get remainder 1
- Bring down two zeros (making it 100)
- Double the quotient (1 becomes 2) and write it with a blank space (2_)
- Find the largest digit (4) such that 24 × 4 = 96 ≤ 100
- Subtract: 100 - 96 = 4, bring down two more zeros
- Continue the process to get more decimal places
- Result: √2 ≈ 1.414
Calculation Tip
For most practical purposes, using √2 ≈ 1.414 is accurate enough. Calculators use more precise values.
Is √2 Rational or Irrational?

√2 is a famous example of an irrational number. But what does that mean?
Rational numbers can be written as fractions (like 1/2 or 3/4) or as terminating or repeating decimals (like 0.5 or 0.333...).
Irrational numbers cannot be written as fractions. Their decimal representations go on forever without repeating.
Why is √2 irrational? Let's see why it can't be written as a fraction:
Imagine √2 could be written as a fraction a/b where a and b are whole numbers with no common factors.
Then (a/b)² = 2 → a² = 2b²
This means a² is even, so a must be even (since only even numbers have even squares).
Let a = 2k, then (2k)² = 2b² → 4k² = 2b² → 2k² = b²
Now b² is even, so b must be even too.
But if both a and b are even, they have a common factor (2), which contradicts our original statement.
Therefore, √2 cannot be written as a fraction - it's irrational!
Historical Note
The ancient Greeks discovered that √2 is irrational, which was a surprising discovery at the time!
Square Root Quiz
Test your understanding of square roots with these questions:
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Discovery
The irrationality of √2 was discovered by the ancient Greeks around 500 BC. The Pythagoreans were said to be so disturbed by this discovery that they tried to keep it secret!
Paper Sizes
The international paper size standard (ISO 216) uses the ratio 1:√2. This means when you cut a sheet in half, you get two sheets with the same aspect ratio.
Computing Records
As of 2022, √2 has been calculated to 10 trillion decimal places! This required massive computing power and sophisticated algorithms.
Never-Ending Number
√2 is an irrational number, meaning its decimal representation goes on forever without repeating. No matter how many digits you calculate, there are always more!


