Square Root of 3 (√3) - Definition, Examples, Quiz, FAQ, Trivia
Learn about square roots with simple explanations, calculation methods, and fun practice activities
What is a Square Root?
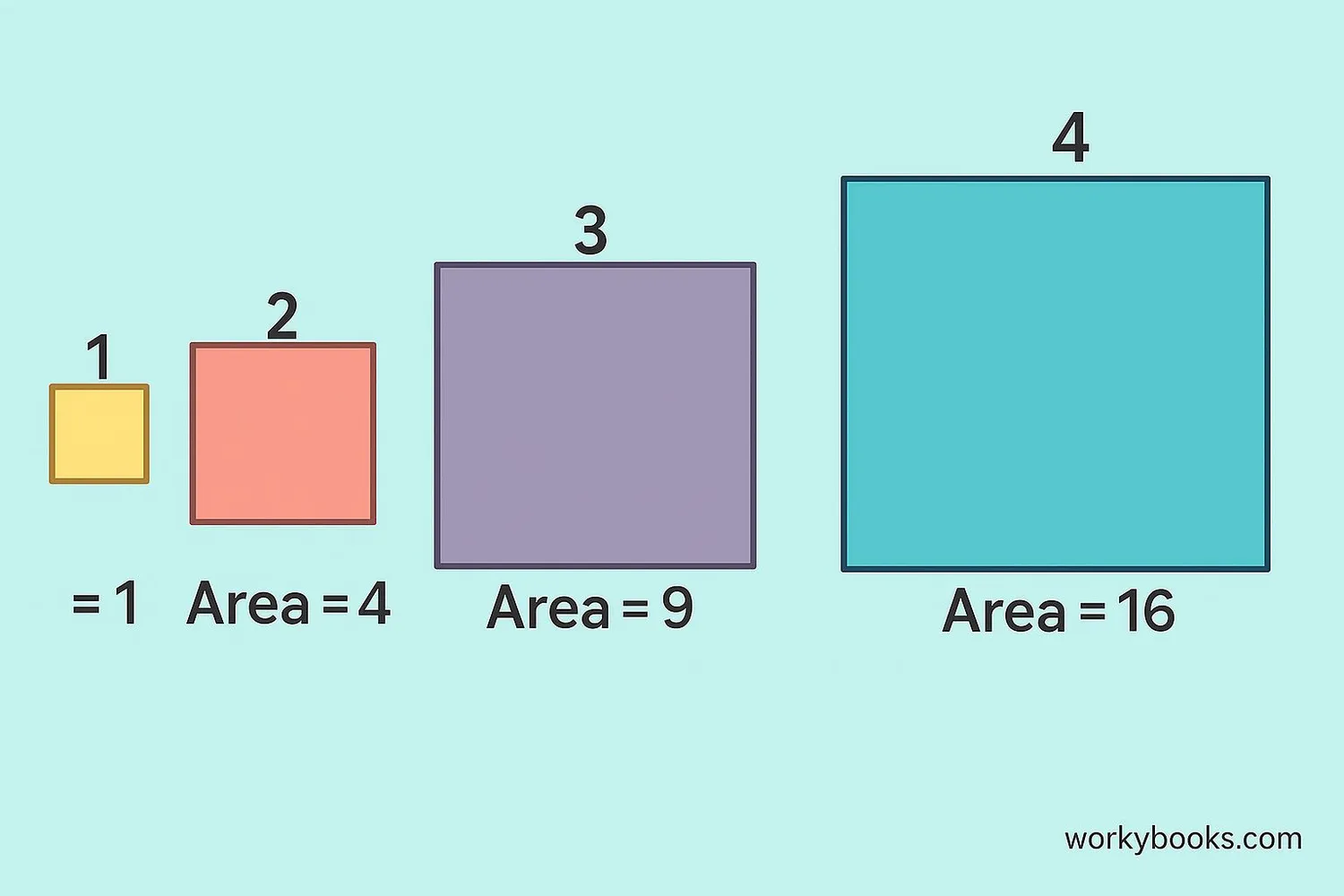
A square root of a number is a value that, when multiplied by itself, gives the original number. It's like asking: "What number times itself equals this number?"
For example:
Because 3 × 3 = 9
Perfect squares like 1, 4, 9, 16, and 25 have whole number square roots. Numbers like 2, 3, 5, and 7 are not perfect squares, so their square roots are decimals that go on forever without repeating.
Key Concept
The square root operation is the opposite of squaring a number.
Square Root of 3
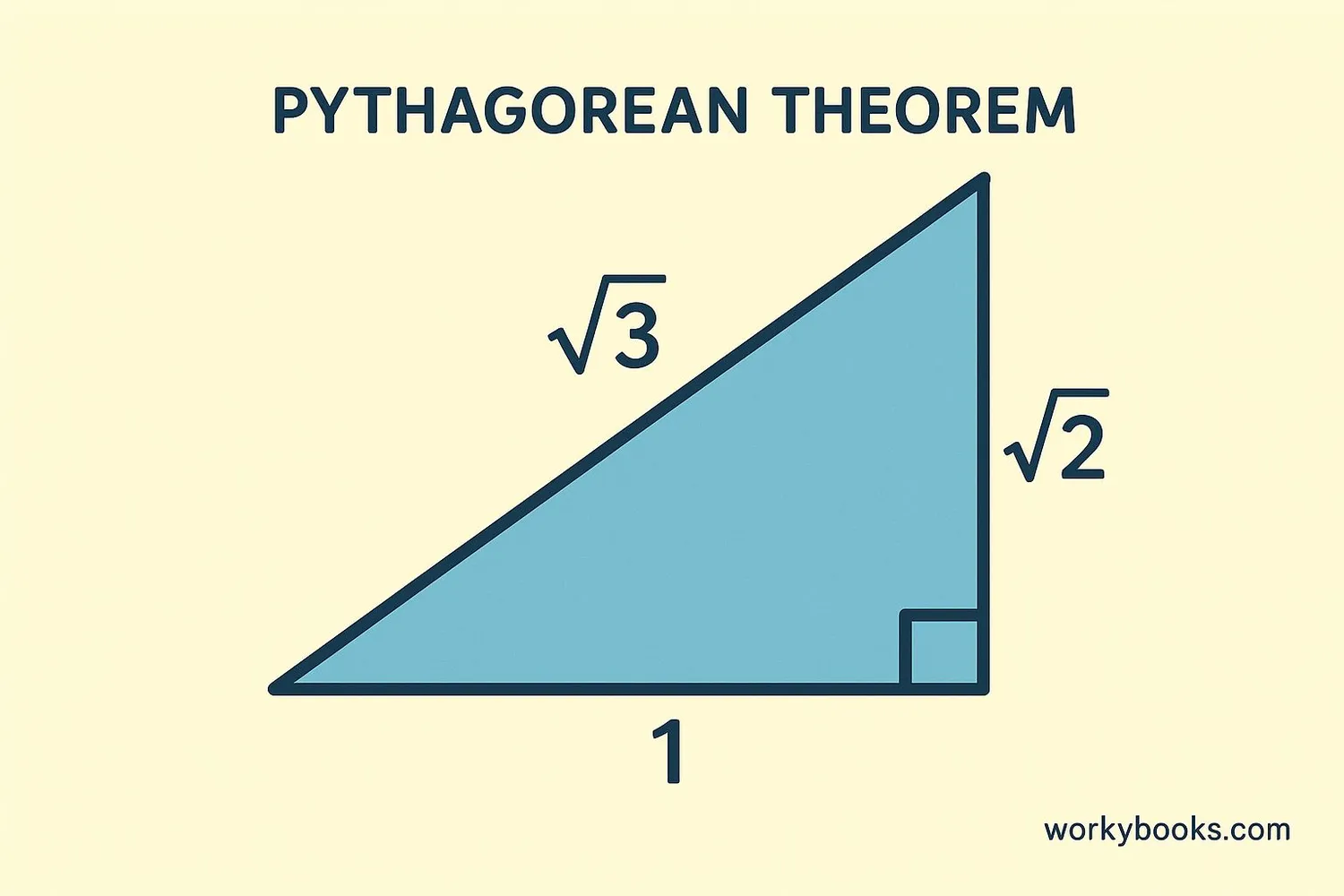
The square root of 3 is the number that when multiplied by itself equals 3. We write it as √3.
- It's an irrational number - its decimal goes on forever without repeating
- It cannot be written as a simple fraction
- It appears in geometry, especially in equilateral triangles
- √3 is greater than 1.7 and less than 1.8
Remember
√3 is irrational because it cannot be expressed as a fraction of two integers.
Methods to Find √3
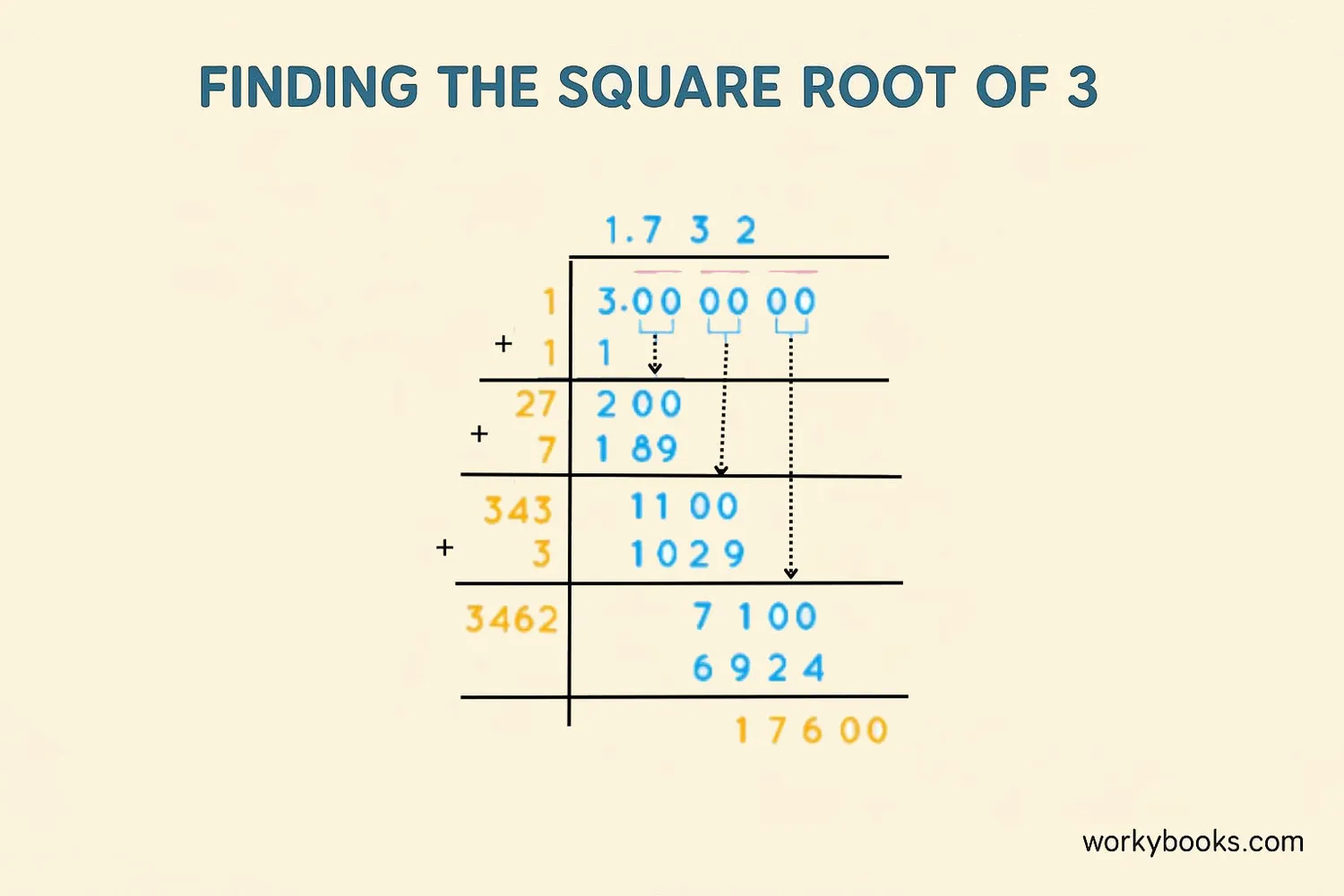
Long Division Method
The long division method is the most accurate way to find square roots by hand. Here's how it works:
Prime Factorization Method
This method works best for perfect squares. Since 3 is prime, we can write:
Method Tip
Long division is the most reliable method for finding square roots of non-perfect squares like 3.
Real-World Examples
The square root of 3 appears in many real-world situations:
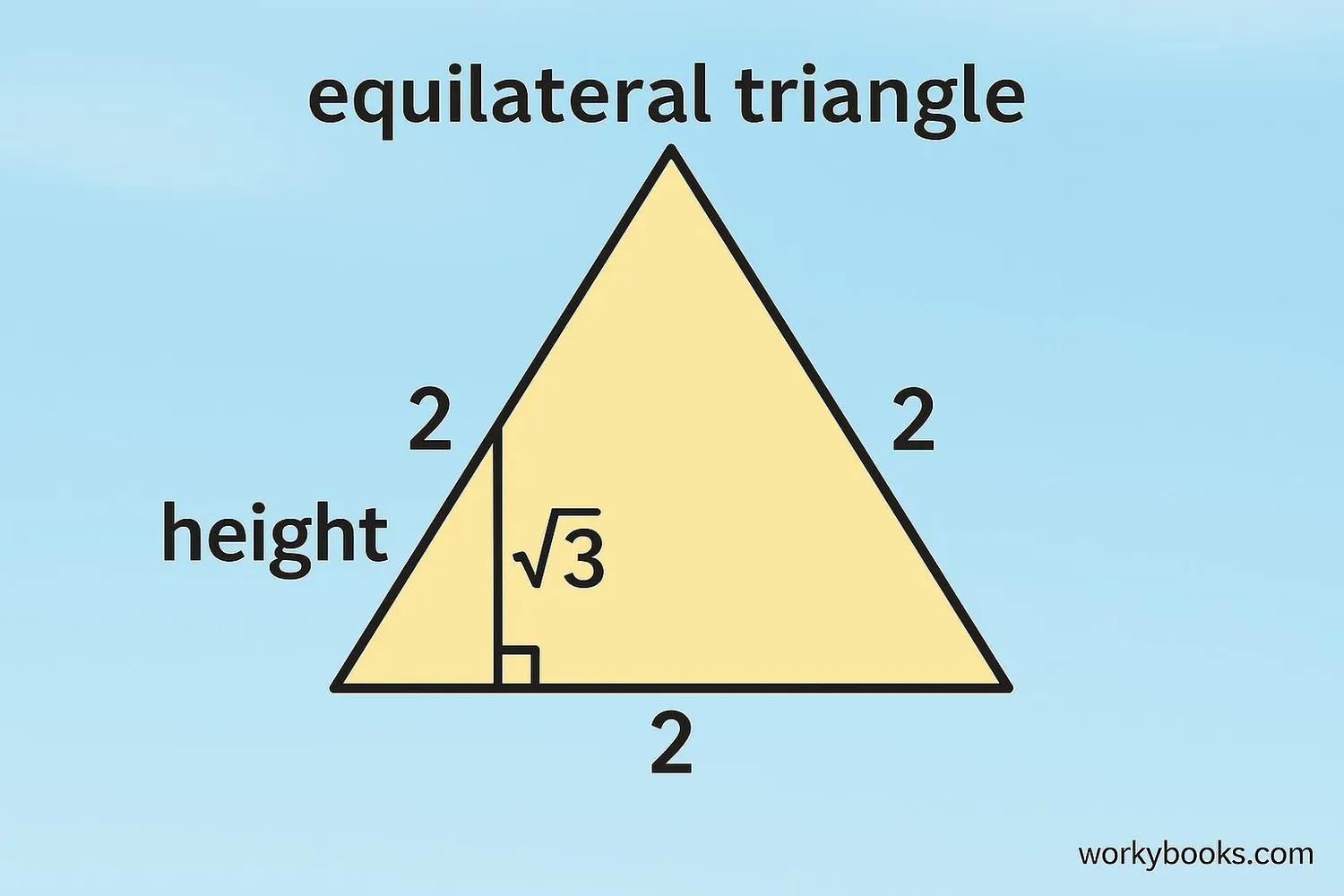
Example 1: Equilateral Triangles
In an equilateral triangle with side length 2, the height is √3 because:
In three-phase power systems, the line-to-line voltage is √3 times the line-to-neutral voltage.
Example 3: Coordinate Geometry
The distance from (0,0) to (1, √3) is √(1² + (√3)²) = √(1 + 3) = √4 = 2
Example 4: Comparing Values
Which is larger: √3 or 1.7? Since 1.7 × 1.7 = 2.89 and 3 > 2.89, √3 > 1.7
Application Tip
√3 often appears in formulas involving triangles with 30°-60°-90° angles.
Square Root Quiz
Test your understanding of square roots with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Square Roots
The Babylonians were calculating square roots as early as 2000 BCE using clay tablets. Their method was similar to the long division method we use today.
Golden Ratio Connection
√3 appears in the calculation of the golden ratio, which is found throughout nature in patterns like sunflower seeds and nautilus shells.
Three-Dimensional Geometry
√3 appears in the spatial diagonal of a cube. For a cube with side length 1, the diagonal through its interior is √3.
Calculating Digits
As of 2023, √3 has been calculated to over 10 trillion decimal places using supercomputers!





