Square Root of 5 - Definition, Examples, Quiz, FAQ, Trivia
Learn what the square root of 5 is with easy explanations, examples, and practice activities
What is the Square Root of 5?
The square root of 5 (√5) is the number that, when multiplied by itself, equals 5.
√5 × √5 = 5
The square root of 5 is an irrational number, which means it cannot be written as a simple fraction and its decimal form goes on forever without repeating. The approximate value is:
√5 ≈ 2.2360679775...
We use the radical symbol (√) to show square roots. The number under the radical is called the radicand (in this case, 5).
Square Root Definition
This means √5 is the number that when multiplied by itself gives 5.
Key Concept
√5 is an irrational number approximately equal to 2.236. It cannot be expressed as a simple fraction.
Methods to Find the Square Root of 5

There are several ways to find the square root of 5. Let's look at three main methods:
1. Estimation Method
We know that 2² = 4 and 3² = 9. Since 5 is between 4 and 9, √5 must be between 2 and 3.
Trying 2.2 × 2.2 = 4.84 (too small)
2.3 × 2.3 = 5.29 (too big)
So √5 is between 2.2 and 2.3
2. Long Division Method
This method gives us more precise digits:
1. Write 5 as 5.000000...
2. Find the largest number whose square is ≤ 5 (2)
3. Subtract 4 (2×2) from 5, bring down two zeros
4. Double the divisor (2 becomes 4) and find next digit
5. Continue the process to get more decimal places
This gives us √5 ≈ 2.236...
3. Prime Factorization Method
Since 5 is a prime number, its prime factorization is just 5.
For numbers with perfect square factors, we can simplify square roots, but since 5 has no perfect square factors other than 1, √5 cannot be simplified further.
Remember
The long division method gives the most accurate decimal value for square roots of numbers that aren't perfect squares.
Examples with √5
Let's see how √5 appears in different situations:
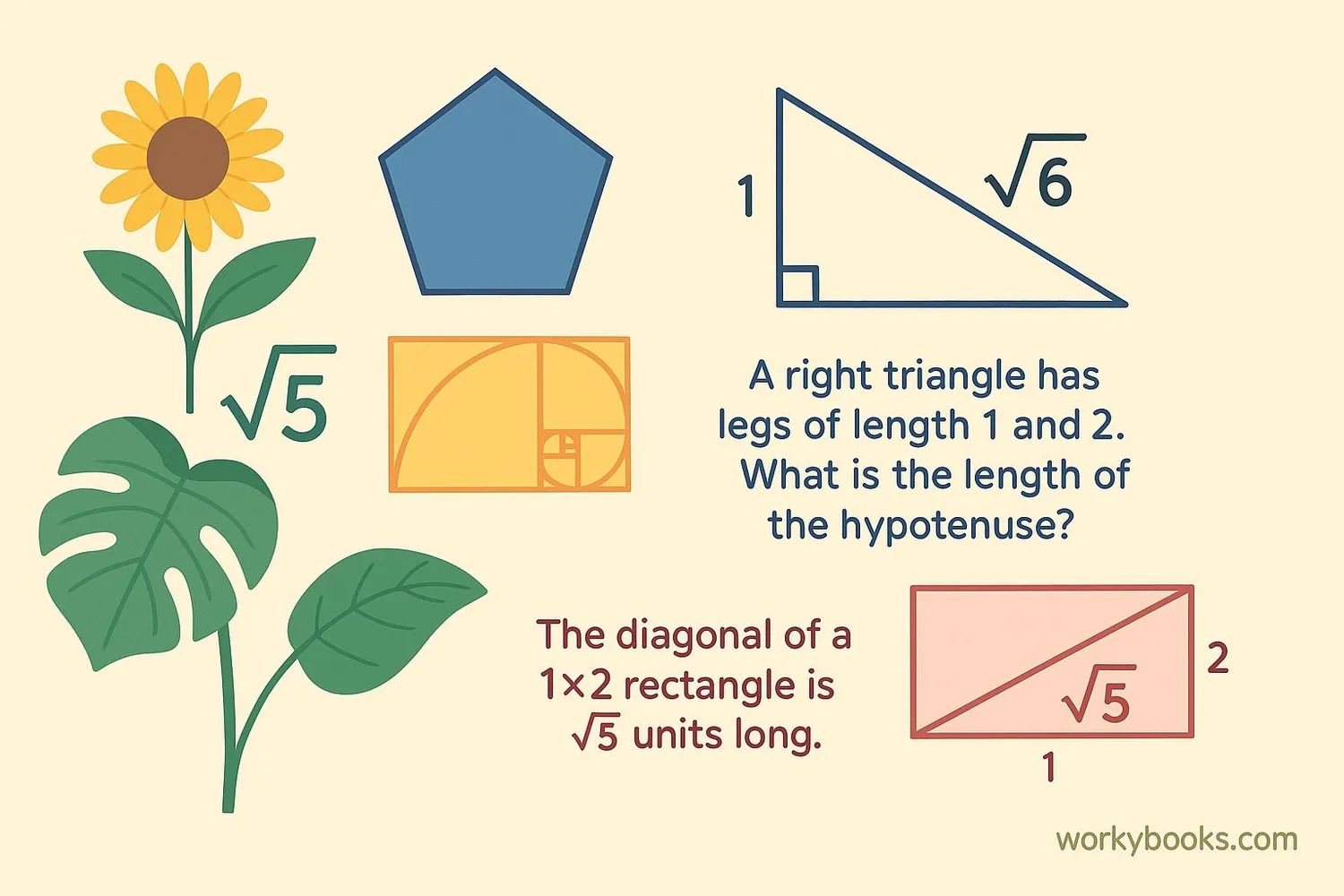
Example 1: A right triangle has legs of length 1 and 2. What is the length of the hypotenuse?
Solution: Using Pythagorean theorem: √(1² + 2²) = √(1 + 4) = √5
Example 2: The golden ratio involves √5 in its calculation:
(1 + √5)/2 ≈ 1.618
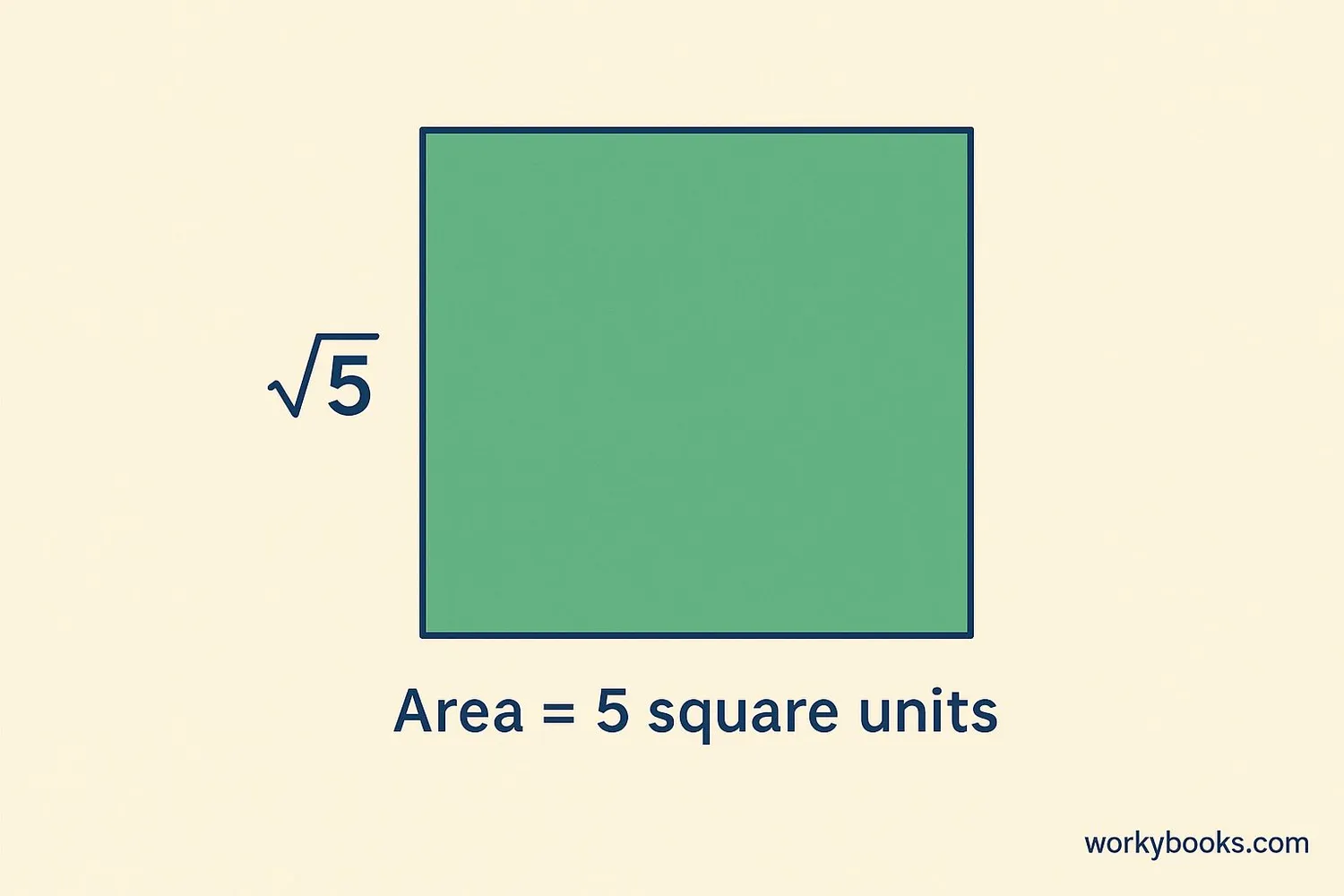
Example 3: If a square has area 5 cm², what is its side length?
Solution: Side length = √5 ≈ 2.236 cm
Example 4: The diagonal of a 1×2 rectangle is √5 units long.
Math Tip
√5 often appears in geometry problems involving right triangles and the golden ratio.
Square Root Quiz
Test your understanding with these 5 questions about square roots:
Frequently Asked Questions
Here are answers to common questions about the square root of 5:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Square Roots
The Babylonians knew how to approximate square roots as early as 1800 BCE. They used a method similar to the modern long division method to calculate √2 with remarkable accuracy.
Golden Ratio
The golden ratio (1 + √5)/2 appears in many natural patterns like sunflower seed arrangements, nautilus shells, and even the proportions of the human body.
Pentagon Connection
The diagonal of a regular pentagon with side length 1 is exactly (1 + √5)/2, the golden ratio. This is why √5 appears in many formulas related to pentagons.
Irrational Discovery
The ancient Greeks were shocked to discover irrational numbers like √2 and √5. According to legend, the Pythagorean who revealed this secret was drowned for revealing this "imperfection" in numbers.





