Square Root of 50 - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate square roots with step-by-step methods and interactive practice
What is a Square Root?
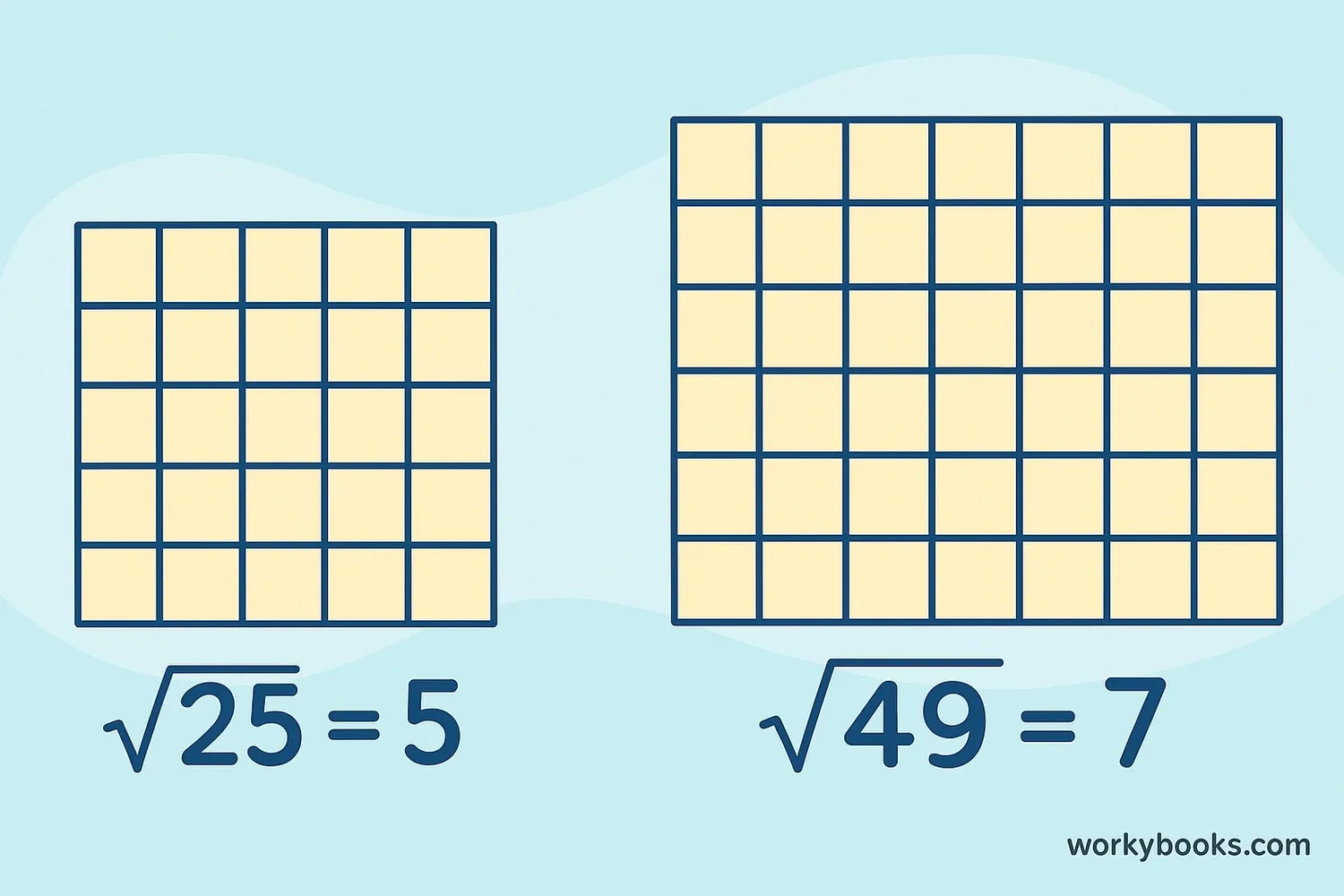
A square root is a number that, when multiplied by itself, gives the original number. It's the opposite of squaring a number. We use the radical symbol (√) to show square roots.
For example:
√25 = 5 because 5 × 5 = 25
√36 = 6 because 6 × 6 = 36
The number inside the radical symbol (√) is called the radicand. When we see √50, it means we're looking for a number that when multiplied by itself equals 50.
Key Concept
Square roots help us find the side length of a square when we know its area. If a square has an area of 50 square units, each side is √50 units long.
Simplifying Square Root of 50
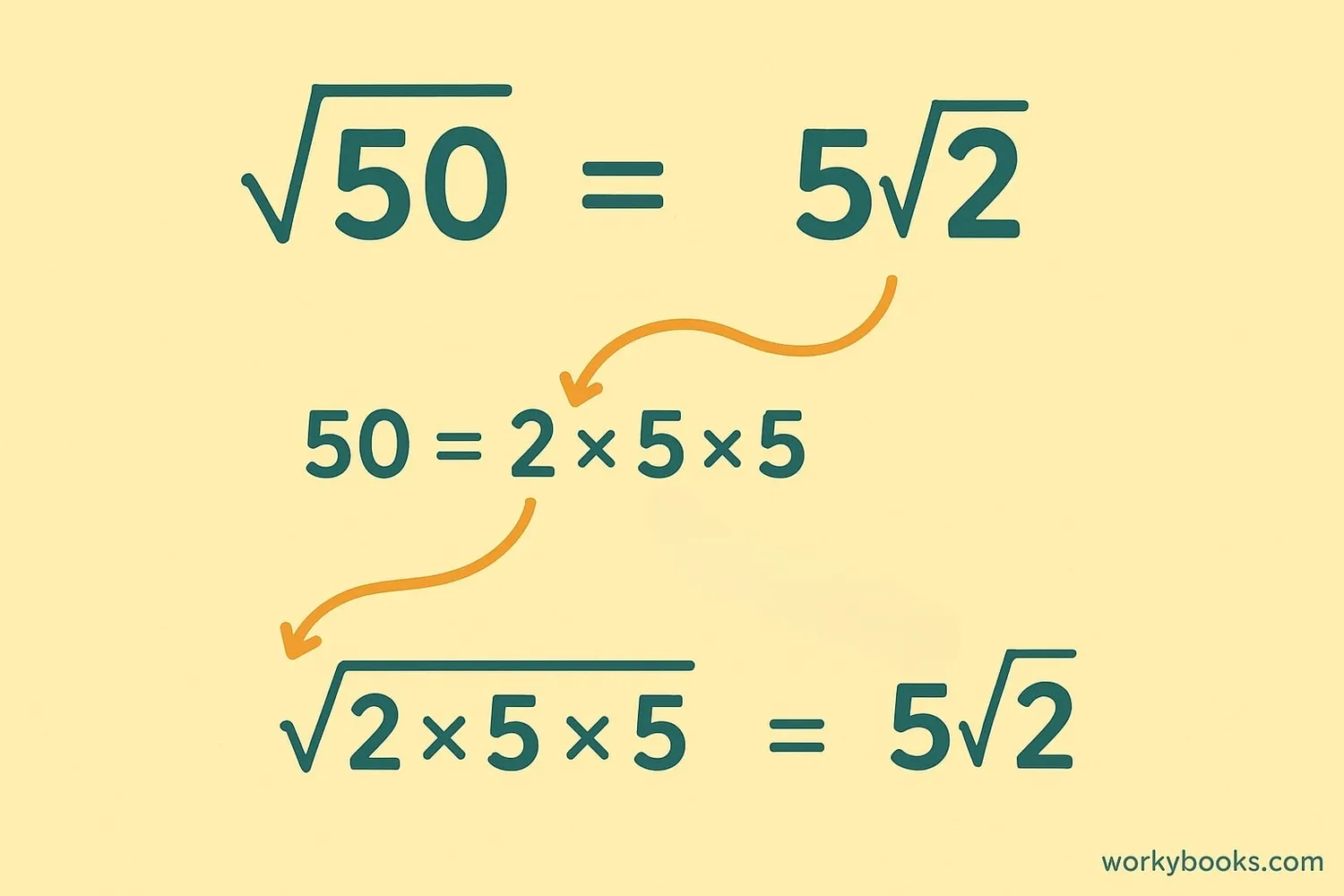
The square root of 50 is not a whole number because 50 is not a perfect square. But we can simplify it to a simpler form:
Simplified Form
This simplified form is easier to work with in math problems.
We find this using prime factorization:
50 = 2 × 5 × 5
√50 = √(2 × 5²) = 5√2
Since 5² is a perfect square, we can take 5 out of the radical, leaving √2 inside.
Remember
We always simplify square roots by factoring out perfect squares. The simplified form has no perfect square factors other than 1 in the radicand.
Methods to Find Square Root of 50
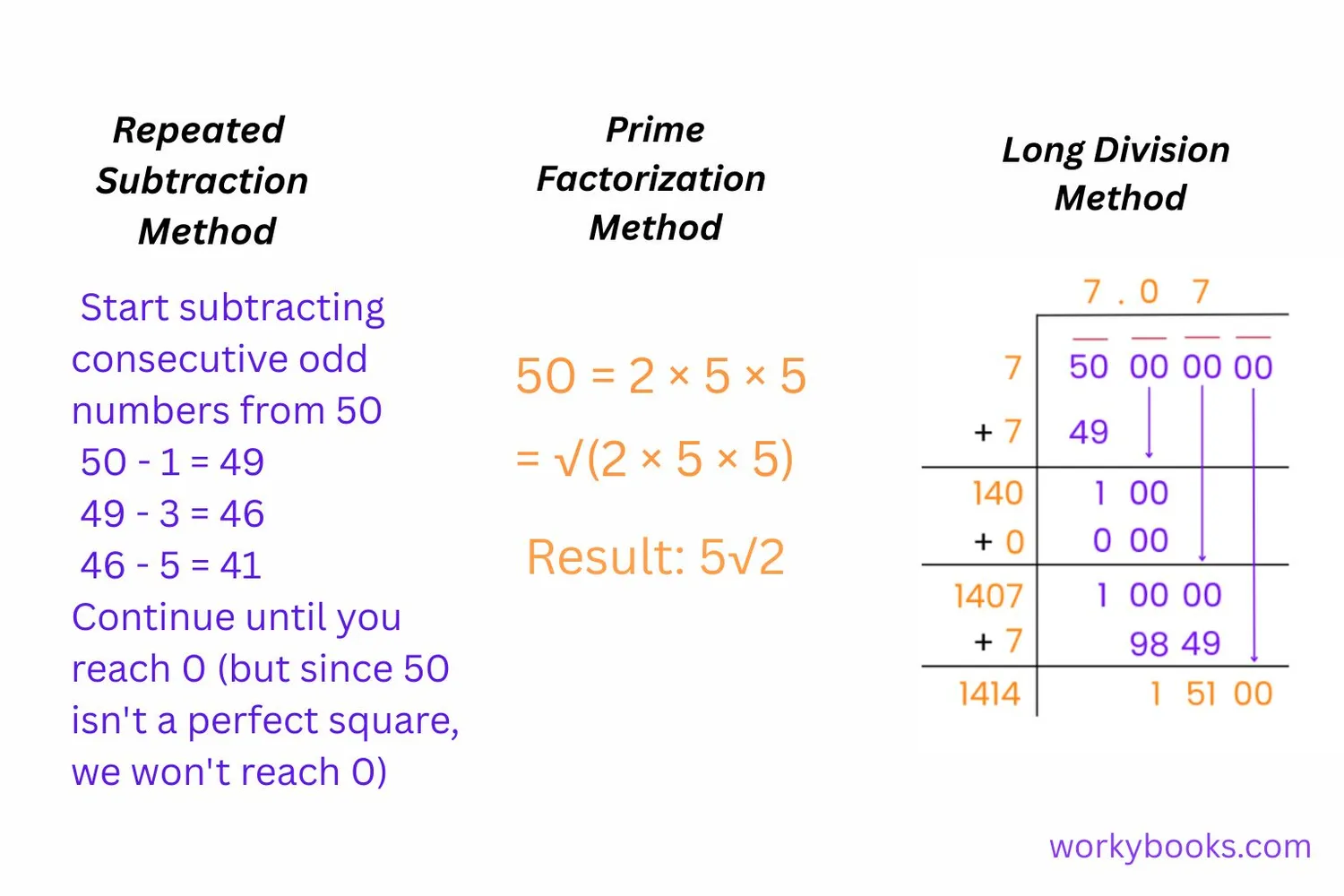
There are several ways to find the square root of 50. Let's explore three common methods:
1. Prime Factorization Method
- 1 Factor 50 into prime numbers: 50 = 2 × 5 × 5
- 2 Group the prime factors in pairs: (5 × 5) × 2
- 3 Take one number from each pair: 5
- 4 Multiply these numbers: 5
- 5 Multiply the remaining factors inside the radical: √2
- 6 Result: 5√2
2. Long Division Method
- 1 Place a bar over 50, grouping digits in pairs
- 2 Find the largest number whose square is ≤ 50 (7, since 7×7=49)
- 3 Subtract 49 from 50, bring down two zeros (making it 100)
- 4 Double the quotient (7 becomes 14) and find a digit (X) so that (140 + X) × X ≤ 1000
- 5 Continue the process to get more decimal places
- 6 Result: √50 ≈ 7.071
3. Repeated Subtraction Method
- 1 Start subtracting consecutive odd numbers from 50
- 2 50 - 1 = 49
- 3 49 - 3 = 46
- 4 46 - 5 = 41
- 5 Continue until you reach 0 (but since 50 isn't a perfect square, we won't reach 0)
- 6 The number of subtractions before passing 0 gives the whole number part
Method Tip
Prime factorization is best for simplifying roots, while long division gives the decimal value. Repeated subtraction helps understand the concept.
Is √50 Rational or Irrational?

The square root of 50 is an irrational number. Here's why:
Rational numbers can be expressed as fractions (a/b where a and b are integers, b≠0). They have terminating or repeating decimals.
Irrational numbers cannot be expressed as fractions. Their decimals go on forever without repeating.
Since 50 is not a perfect square, √50 cannot be expressed as a fraction. Its decimal form is 7.071067811865475... which goes on forever without repeating.
Key Point
This never-ending, non-repeating decimal confirms it's irrational.
Remember
Square roots of perfect squares (1, 4, 9, 16, 25, etc.) are rational. Square roots of other whole numbers are irrational.
Examples and Applications
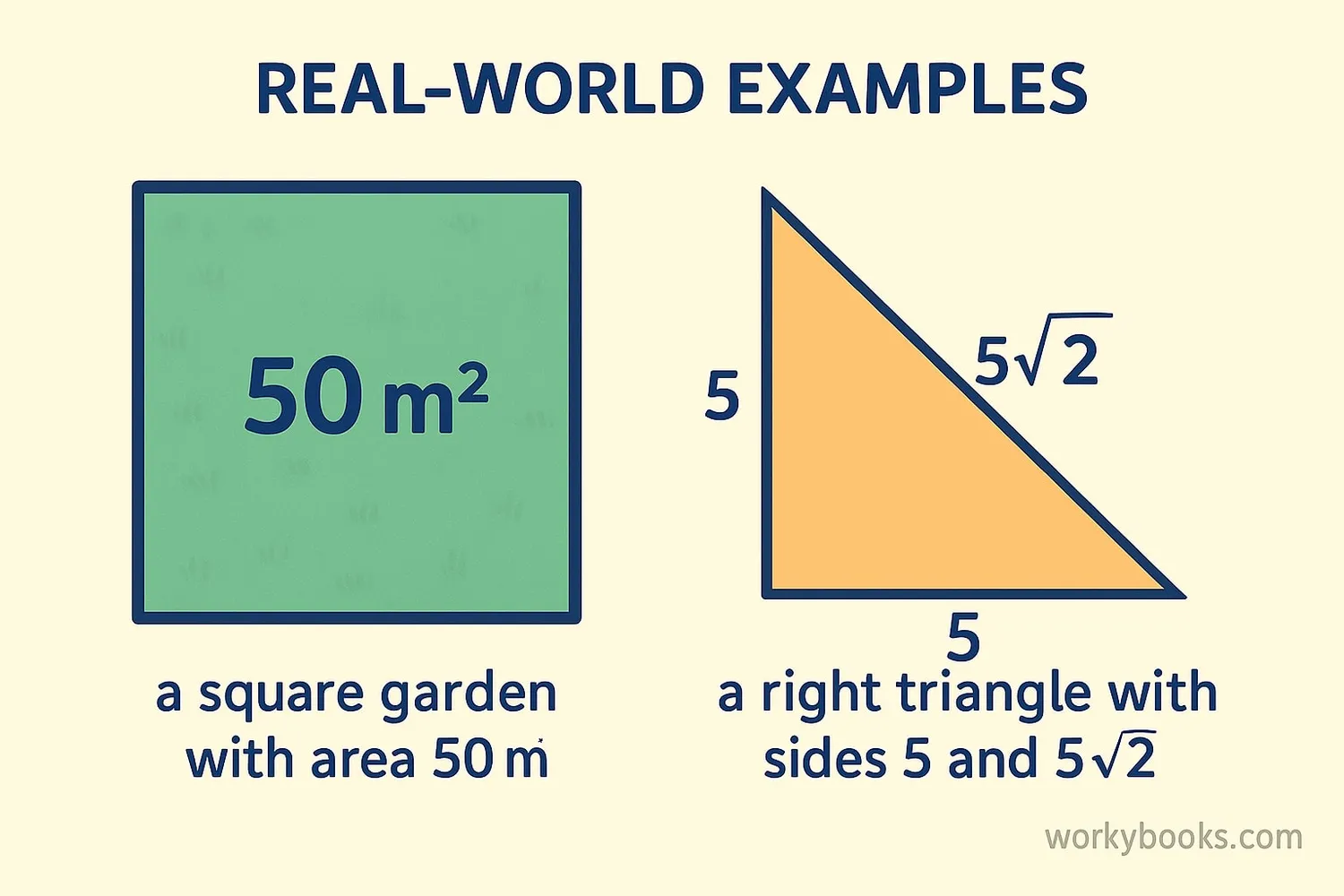
Let's see how we use square roots like √50 in real situations:
Example 1: A square garden has an area of 50 square meters. How long is each side?
Solution: Side length = √50 ≈ 7.071 meters
Example 2: In a right triangle with two equal sides of 5 units, how long is the hypotenuse?
Solution: Hypotenuse = √(5² + 5²) = √(25 + 25) = √50 = 5√2 ≈ 7.071 units
Example 3: A square painting has sides of 5 feet. How long is the diagonal?
Solution: Diagonal = √(5² + 5²) = √(25 + 25) = √50 = 5√2 ≈ 7.071 feet
Example 4: Simplify 2√50
Solution: 2√50 = 2 × √(25 × 2) = 2 × 5√2 = 10√2
Math Tip
Square roots often appear in geometry problems involving distances, diagonals, and the Pythagorean theorem.
Square Root Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and numbers:
Ancient Square Roots
The Babylonians calculated square roots as far back as 1800 BCE! They used a method similar to long division on clay tablets.
Irrational Discovery
The ancient Greeks were shocked to discover irrational numbers like √2. According to legend, the mathematician who revealed this was drowned for sharing the "dangerous" knowledge!
Square Root Symbol
The radical symbol (√) for square roots was first used in 1525 by mathematician Christoph Rudolff. It may have evolved from the letter "r" for "radix" (Latin for root).
Pi Connection
Did you know √10 is approximately π? √10 ≈ 3.162 while π ≈ 3.1416. This coincidence was used in ancient times when π was less accurately known.





