Square Root of 6 (√6) - Definition, Examples, Quiz, FAQ, Trivia
Learn what square roots are and how to find the square root of 6 with step-by-step methods
What is a Square Root?
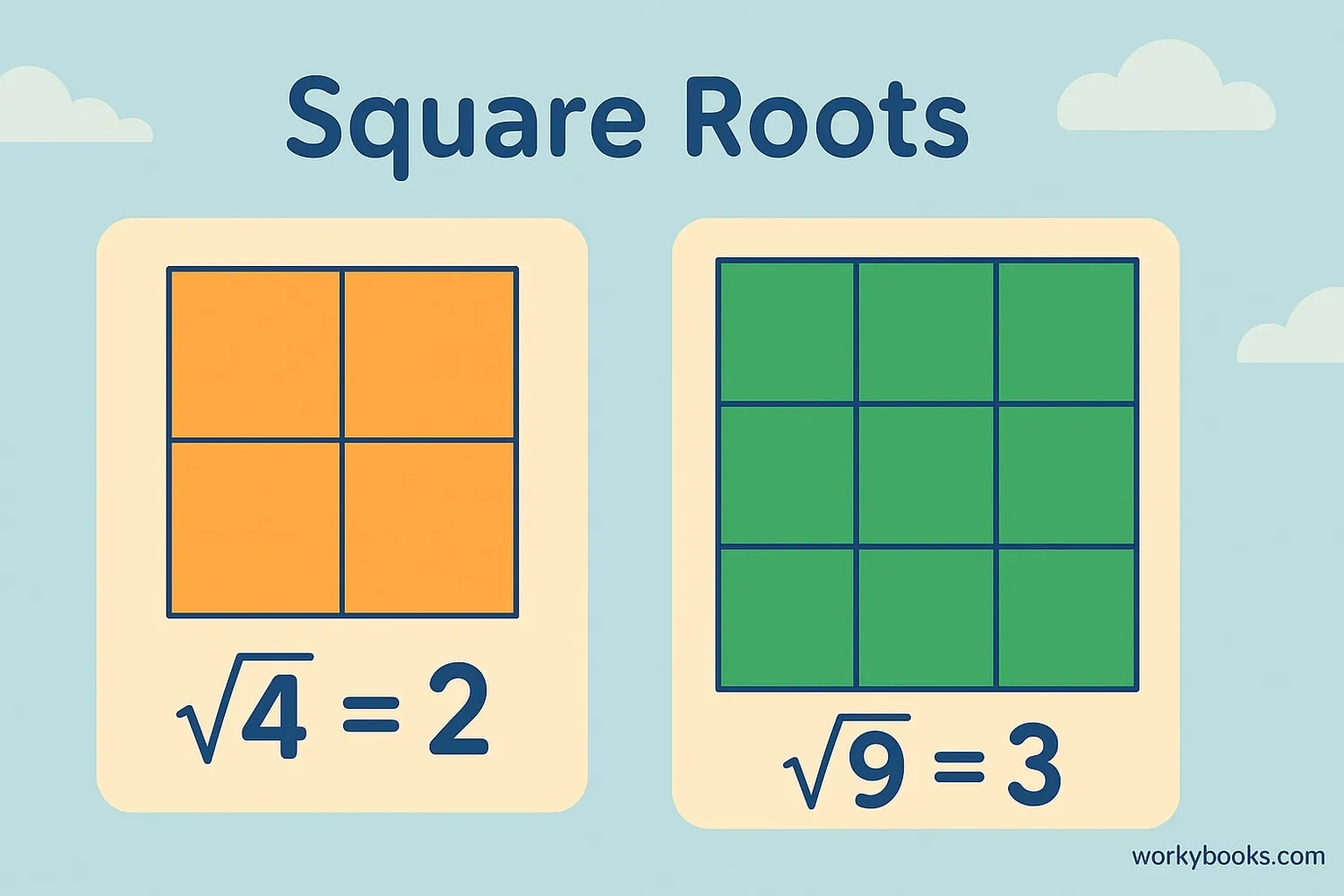
A square root is a special number that, when multiplied by itself, gives the original number.
For example:
- The square root of 9 is 3 because 3 × 3 = 9
- The square root of 16 is 4 because 4 × 4 = 16
- The square root of 25 is 5 because 5 × 5 = 25
We use the radical symbol (√) to represent square roots. The number under the radical symbol is called the radicand. For √6, 6 is the radicand.
Key Concept
Square roots are the opposite of squaring a number. If 3² = 9, then √9 = 3.
What is the Square Root of 6?
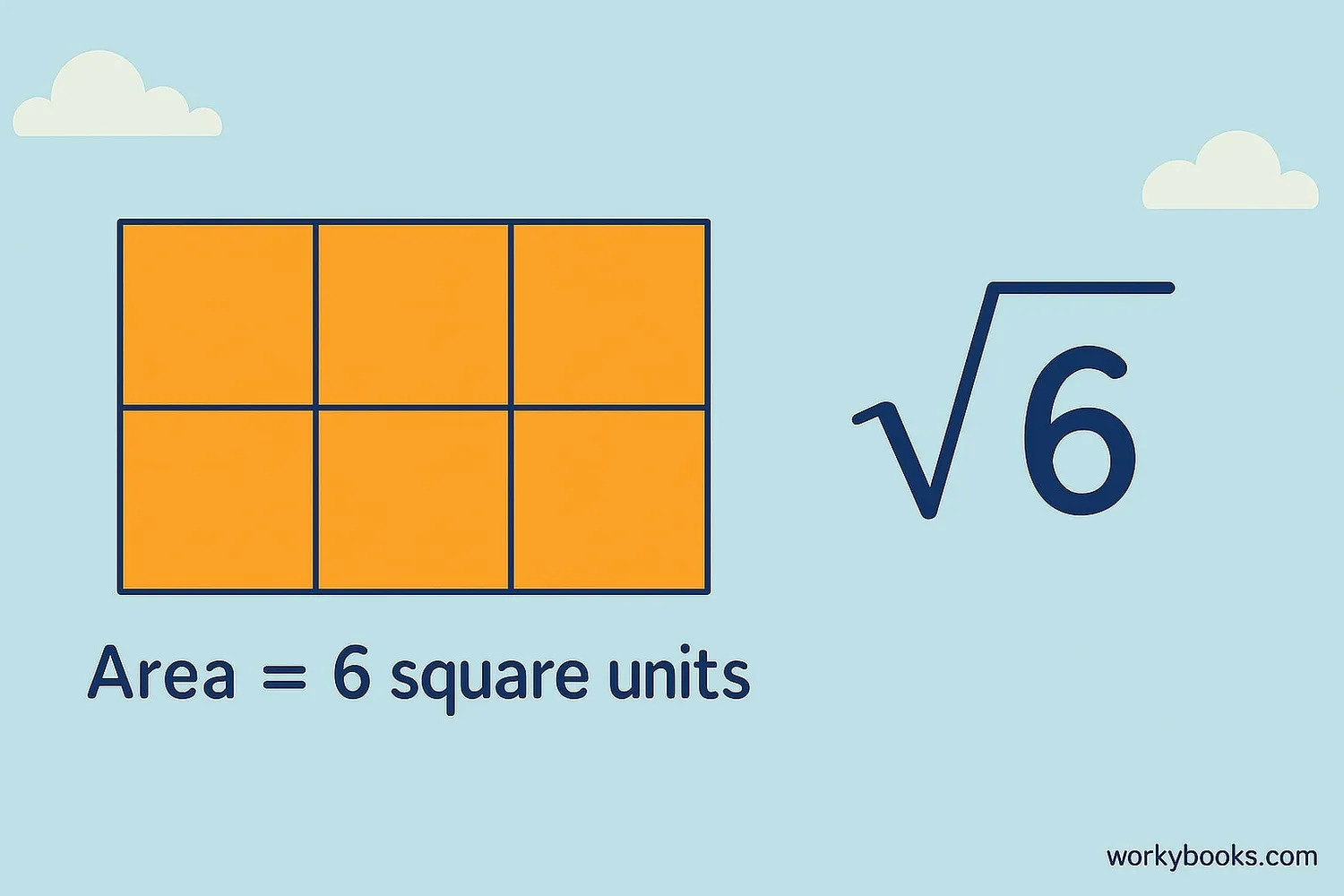
The square root of 6 is written as √6. Its value is approximately 2.449.
This means that 2.449 × 2.449 ≈ 6. Since 6 is not a perfect square (like 4, 9, or 16),
its square root is not a whole number. We call numbers like 6 imperfect squares.
Here are some important facts about √6:
- √6 ≈ 2.44948974278 (this decimal goes on forever without repeating)
- √6 is greater than √4 (which is 2) and less than √9 (which is 3)
- Both positive and negative numbers can be square roots: -2.449 × -2.449 also equals 6
Square Root of 6
This is the principal (positive) square root of 6
How to Find the Square Root of 6



There are several ways to find the square root of 6. Let's explore three methods:
1. Repeated Subtraction Method
- Start with 6 and subtract consecutive odd numbers: 6 - 1 = 5
- 5 - 3 = 2
- 2 - 5 = -3 (negative number, so we stop)
- We subtracted twice before getting a negative number
- This method works only for perfect squares, so for 6 it shows it's not a perfect square
2. Prime Factorization Method
- Find the prime factors of 6: 6 = 2 × 3
- Group the factors in pairs: 2 and 3 are different
- Since there are no identical pairs, 6 is not a perfect square
- The square root would be √(2 × 3) = √2 × √3 ≈ 1.414 × 1.732 ≈ 2.449
3. Long Division Method
- Set up 6 in pairs of digits: 06.00 00 00
- Find the largest number whose square is ≤ 6 (2, since 2²=4)
- Subtract: 6 - 4 = 2, bring down 00 → 200
- Double the quotient (2×2=4), find digit X such that (40 + X) × X ≤ 200 → 4 (44×4=176)
- Subtract: 200 - 176 = 24, bring down 00 → 2400
- Double quotient (24×2=48), find X such that (480 + X) × X ≤ 2400 → 4 (484×4=1936)
- Continue to get √6 ≈ 2.449
Remember
The long division method is the most accurate way to find square roots of non-perfect squares like 6.
Is √6 Rational or Irrational?

√6 is an irrational number. This means:
- It cannot be written as a simple fraction (like 1/2 or 3/4)
- Its decimal representation goes on forever without repeating
- √6 ≈ 2.44948974278... and the decimal never repeats or ends
Why is √6 irrational?
If √6 could be written as a fraction a/b (where a and b are whole numbers with no common factors), then 6 = a²/b², so 6b² = a². This would mean a² is divisible by 2 and 3, so a would need to be divisible by 2 and 3. But then b would also need to be divisible by 2 and 3, which contradicts our assumption that a and b have no common factors. Therefore, √6 cannot be written as a fraction and is irrational.
Important Fact
The square root of any whole number is either an integer (if it's a perfect square) or irrational.
Examples and Practice
Let's practice with some examples:
Example 1: A square has an area of 6 square meters. How long is each side?
Solution: Side length = √6 ≈ 2.449 meters
Example 2: Compare √6 and 2.5
Solution: √6 ≈ 2.449 which is less than 2.5
Example 3: What number squared gives you 6?
Solution: √6 ≈ 2.449 (since 2.449 × 2.449 ≈ 6)
Example 4: Is 2.449 the exact square root of 6?
Solution: No, 2.449 is an approximation. The actual √6 has an infinite number of decimal places.
Example 5: Between which two consecutive integers does √6 lie?
Solution: Since 2² = 4 and 3² = 9, and 4 < 6 < 9, so √6 is between 2 and 3.
Practice Tip
Try calculating √6 using the long division method to see how the decimal places are determined!
Square Root Quiz
Test your understanding of square roots with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about square roots:
Math Trivia
Discover interesting facts about square roots and mathematics:
Ancient Roots
The concept of square roots dates back to ancient Babylonian mathematics around 1800 BC. Babylonian mathematicians had advanced methods for approximating square roots on clay tablets.
Radical Symbol Origin
The radical symbol (√) was first used in 1525 by mathematician Christoff Rudolff in his book "Coss." The symbol may have evolved from the letter "r" for "radix," the Latin word for root.
Calculation Record
The world record for calculating the most digits of √6 is over 10 trillion decimal places! This calculation requires supercomputers and sophisticated algorithms.
Practical Applications
Square roots like √6 are essential in architecture for calculating diagonal distances, in digital image processing for edge detection, and in physics for determining wave amplitudes.





