Straight Angles in Geometry - Definition, Examples, Quiz, FAQ, Trivia
Learn about 180° angles that form straight lines with easy explanations and practice activities
What is a Straight Angle?

A straight angle is an angle that measures exactly 180 degrees. It's called a "straight" angle because it forms a perfectly straight line. When two rays extend in exactly opposite directions from a common vertex (starting point), they form a straight angle.
Here are some key facts about straight angles:
- Measures exactly 180°
- Forms a straight line
- Is a type of supplementary angle
- Can be thought of as two right angles combined (90° + 90° = 180°)
- In radians (another way to measure angles), it equals π radians
Key Concept
A straight angle is the largest angle that isn't a full rotation. It divides a circle exactly in half.
Properties of Straight Angles
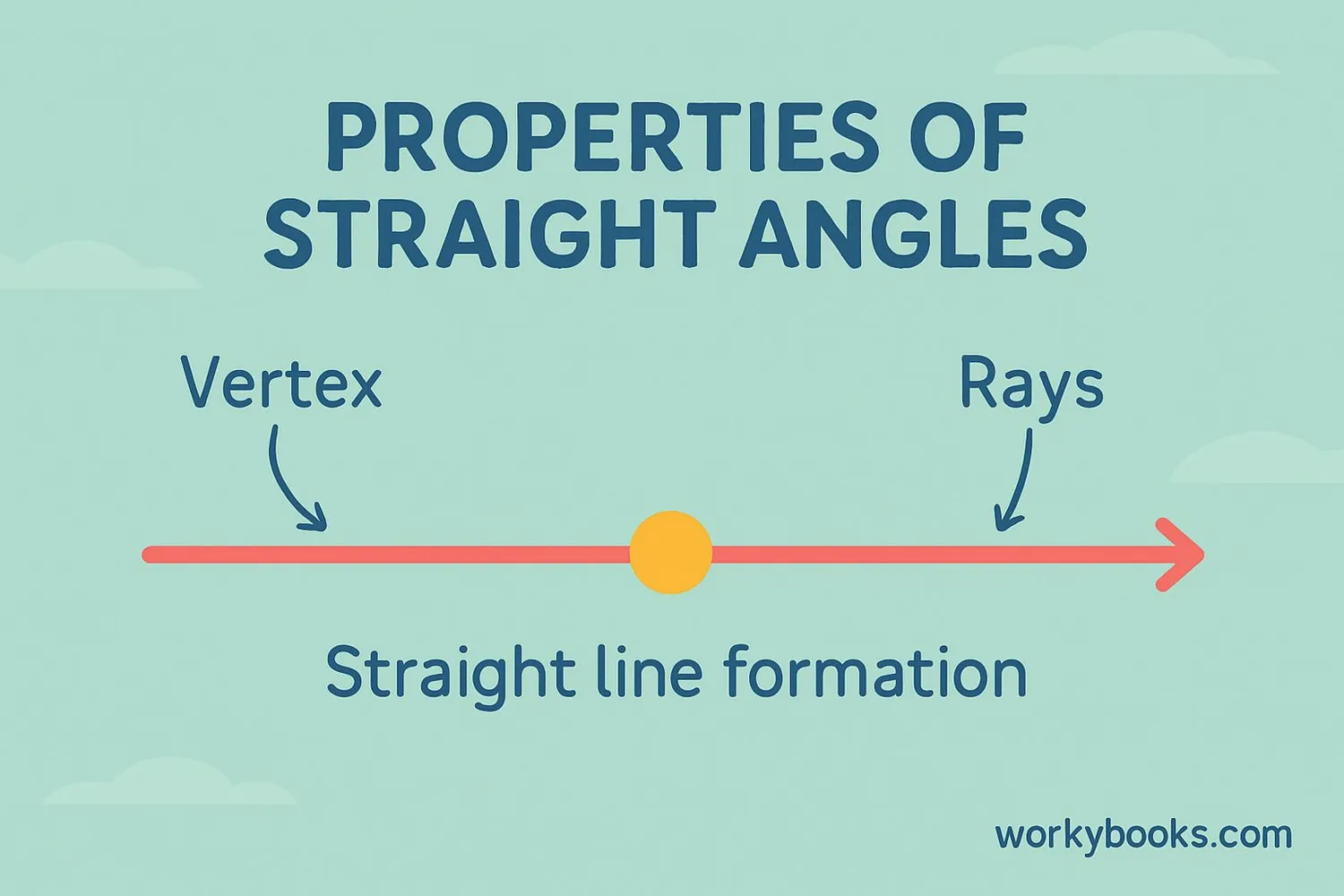
Straight angles have several important properties that make them special in geometry:
1. Always forms a straight line: No matter how long the rays are, they will always form a perfectly straight line.
2. Supplementary angles: Any straight angle can be divided into two angles that add up to 180°. These are called supplementary angles.
3. Straight angle theorem: When two adjacent angles form a straight angle, they are supplementary (their measures add to 180°).
4. Unique appearance: Unlike other angles, a straight angle doesn't have a "bend" or "corner" - it's completely flat.
Remember
A straight angle is the only angle that looks like a straight line. All other angles have some degree of bend.
Types of Angles
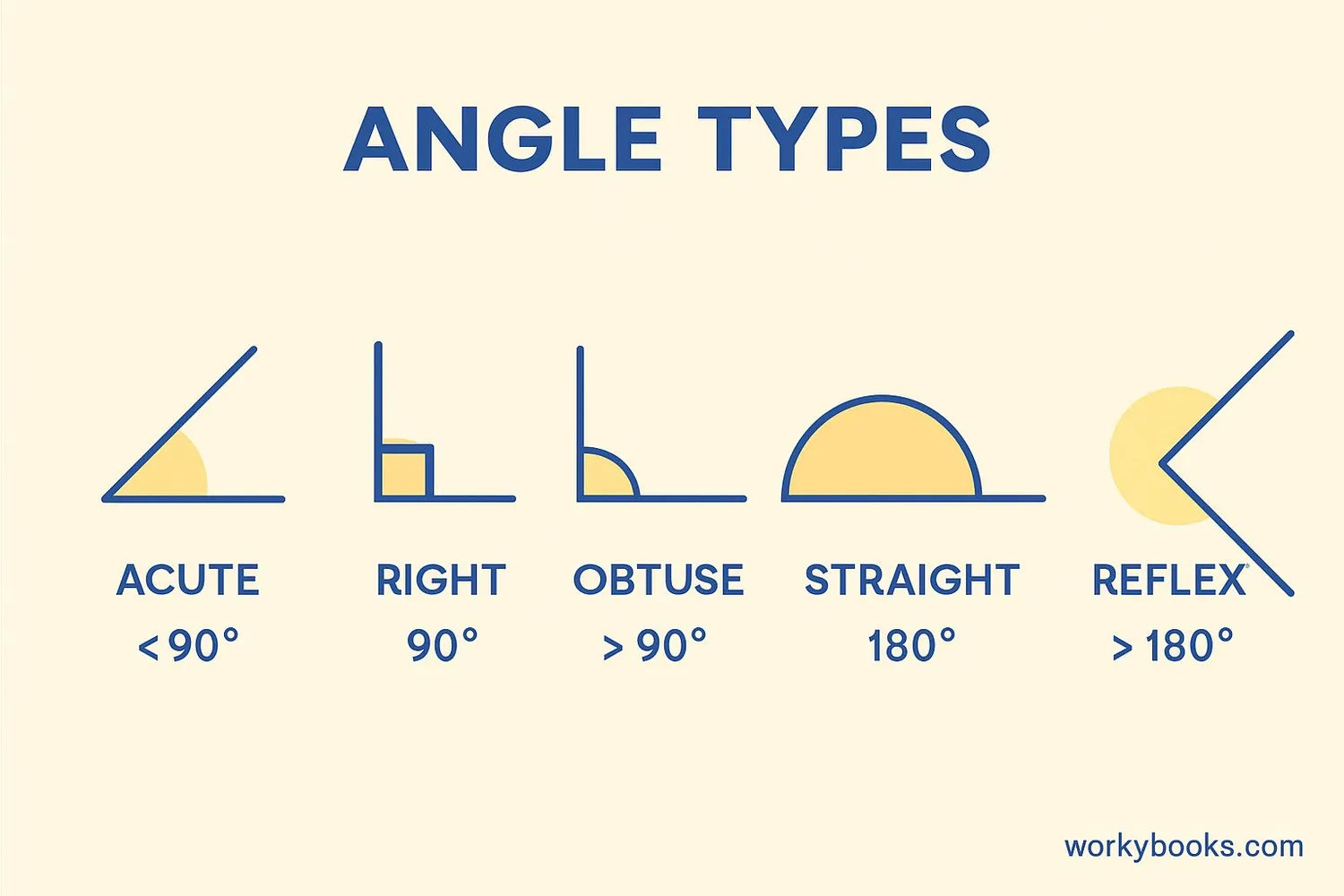
Angles are classified based on their measurement. Let's look at the main types:
| Angle Type | Measurement | Description | Example |
|---|---|---|---|
| Acute Angle | Less than 90° | Smaller than a right angle | Corner of a slice of pizza |
| Right Angle | Exactly 90° | Forms a perfect L-shape | Corner of a book |
| Obtuse Angle | Between 90° and 180° | Wider than a right angle | Open book at 120° |
| Straight Angle | Exactly 180° | Forms a straight line | Open ruler |
| Reflex Angle | Between 180° and 360° | Larger than a straight angle | Clock showing 7:00 |
| Full Angle | Exactly 360° | Complete circle | Ferris wheel after one rotation |
Important Relationship
Two right angles (90° + 90°) make one straight angle (180°).
Real-World Examples
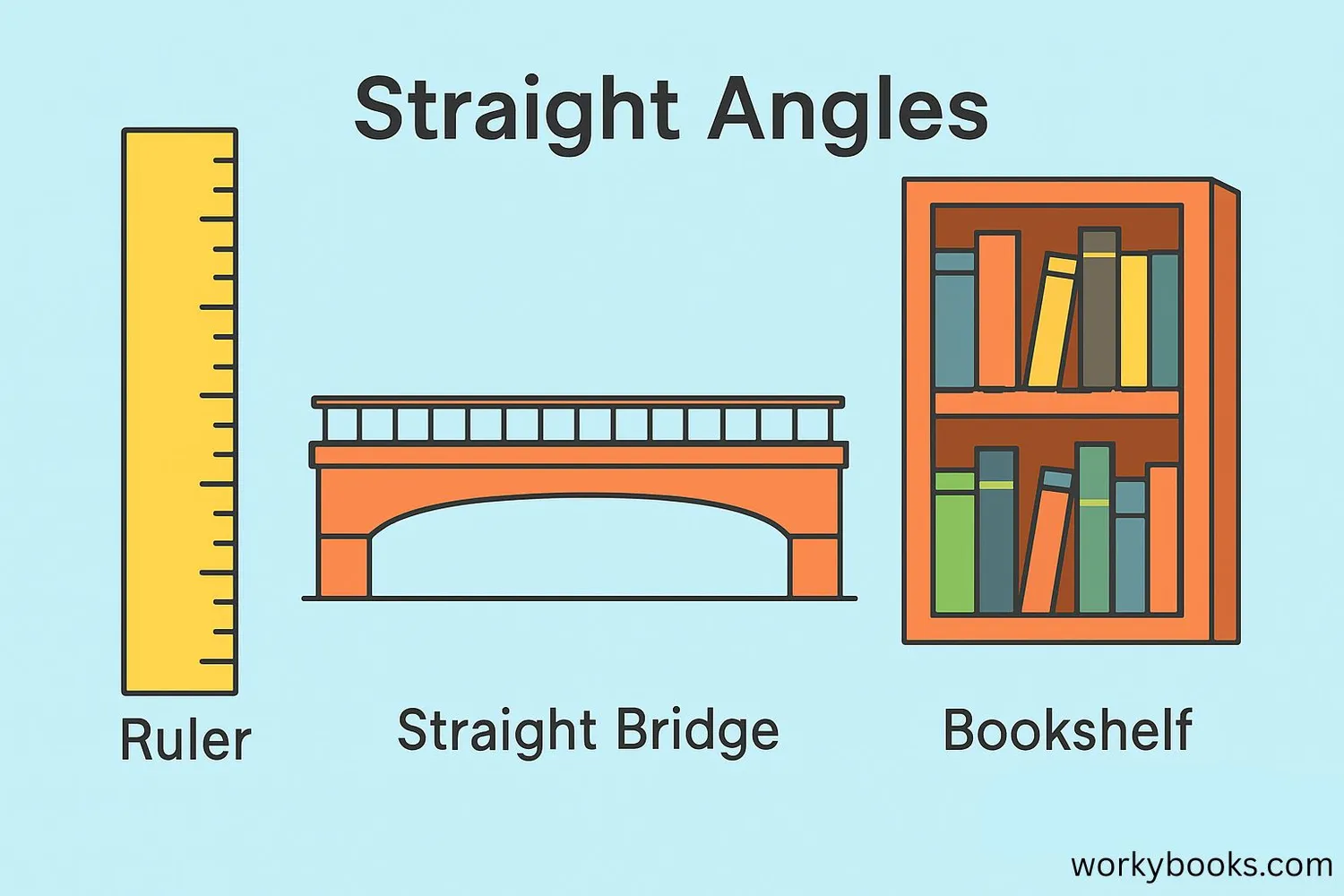
Straight angles are all around us! Here are some common examples you can find in everyday life:
1. Straight ruler: The edge of a ruler forms a perfect straight angle (180°).
2. Table edge: The corner where two sides of a table meet forms a straight angle when viewed from the side.
3. Book opened flat: When you open a book completely flat, the angle between the two covers is 180°.
4. Straight roads: Long, straight sections of roads form straight angles.
5. Door frame: The top edge where the door frame meets the wall forms a straight angle.
6. Horizon line: Where the ocean meets the sky appears as a straight angle across your field of view.
Observation Tip
Look for objects that form perfectly straight lines - they likely contain straight angles!
Straight Angle Practice Quiz
Test your understanding of straight angles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about straight angles:
Angle Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Measurement
The concept of angles dates back to ancient Babylonian astronomers who divided circles into 360 parts around 1800 BC. This is why we have 360 degrees in a circle today!
Angles in Nature
Honeybees build their honeycombs with precise 120° angles, creating perfect hexagons. This shape uses the least amount of wax while storing the most honey.
Angles in Space
Astronomers use angles to measure distances in space. The distance from Earth to nearby stars is measured in "parallax angles" - tiny angles as small as 0.00001 degrees!
Most Precise Angle
Scientists have created angles with precision to one billionth of a degree! This incredible accuracy is used in advanced telescopes and satellite navigation systems.





