Surface Area - Definition, Examples, Quiz, FAQ, Trivia
Learn about surface area with easy explanations, visual examples, and practice activities
What is Surface Area?
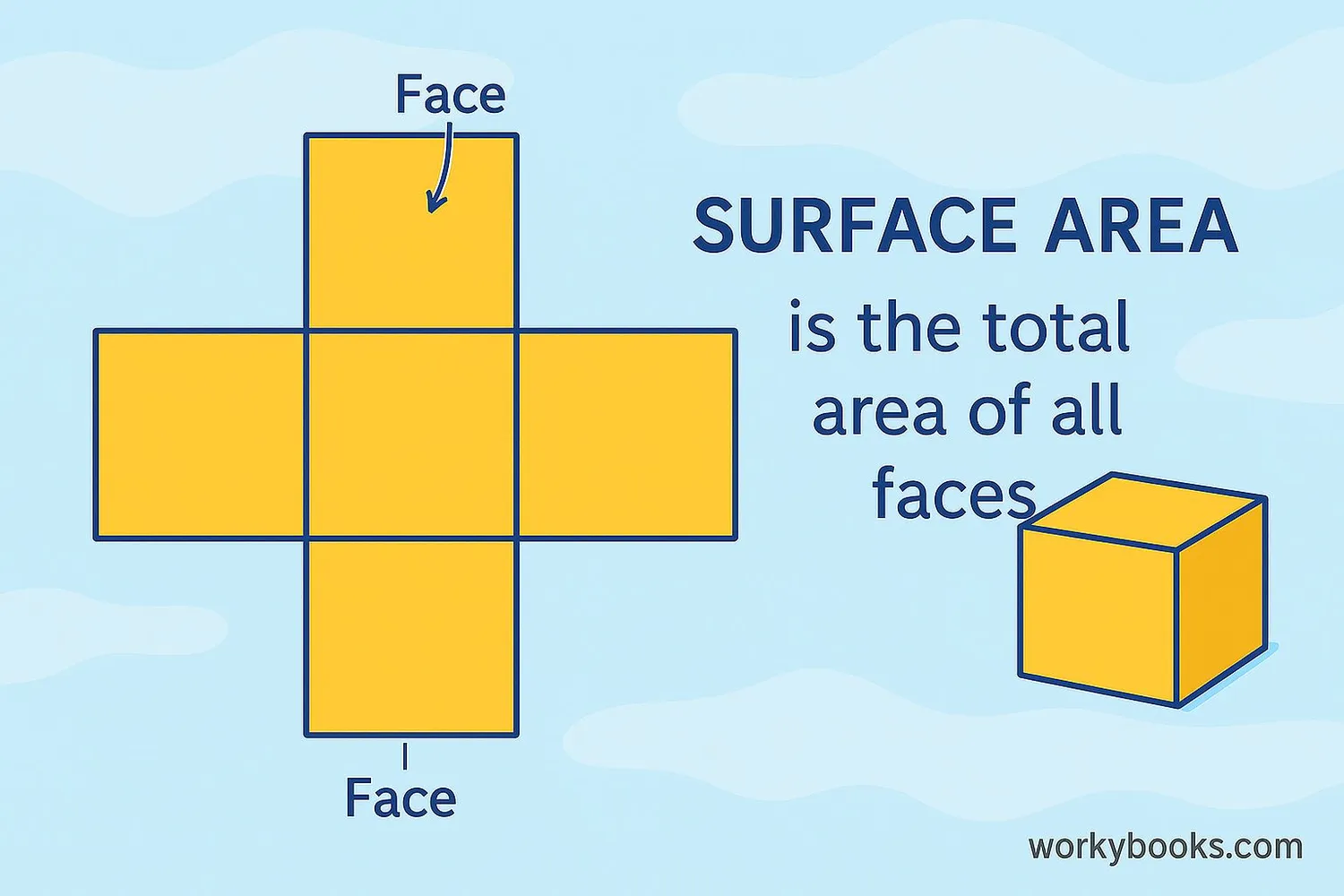
Surface area is the total area that covers the outside of a three-dimensional object. Imagine wrapping a gift - the surface area is how much wrapping paper you would need to cover the entire box without any overlaps.
Why is surface area important? It helps us:
- Calculate how much paint we need to cover an object
- Determine material needed for packaging
- Understand heat transfer in science
- Solve real-world problems in engineering and design
Key Concept
Surface Area = The sum of the areas of all the faces or surfaces that cover a 3D object.
Surface Area Formulas
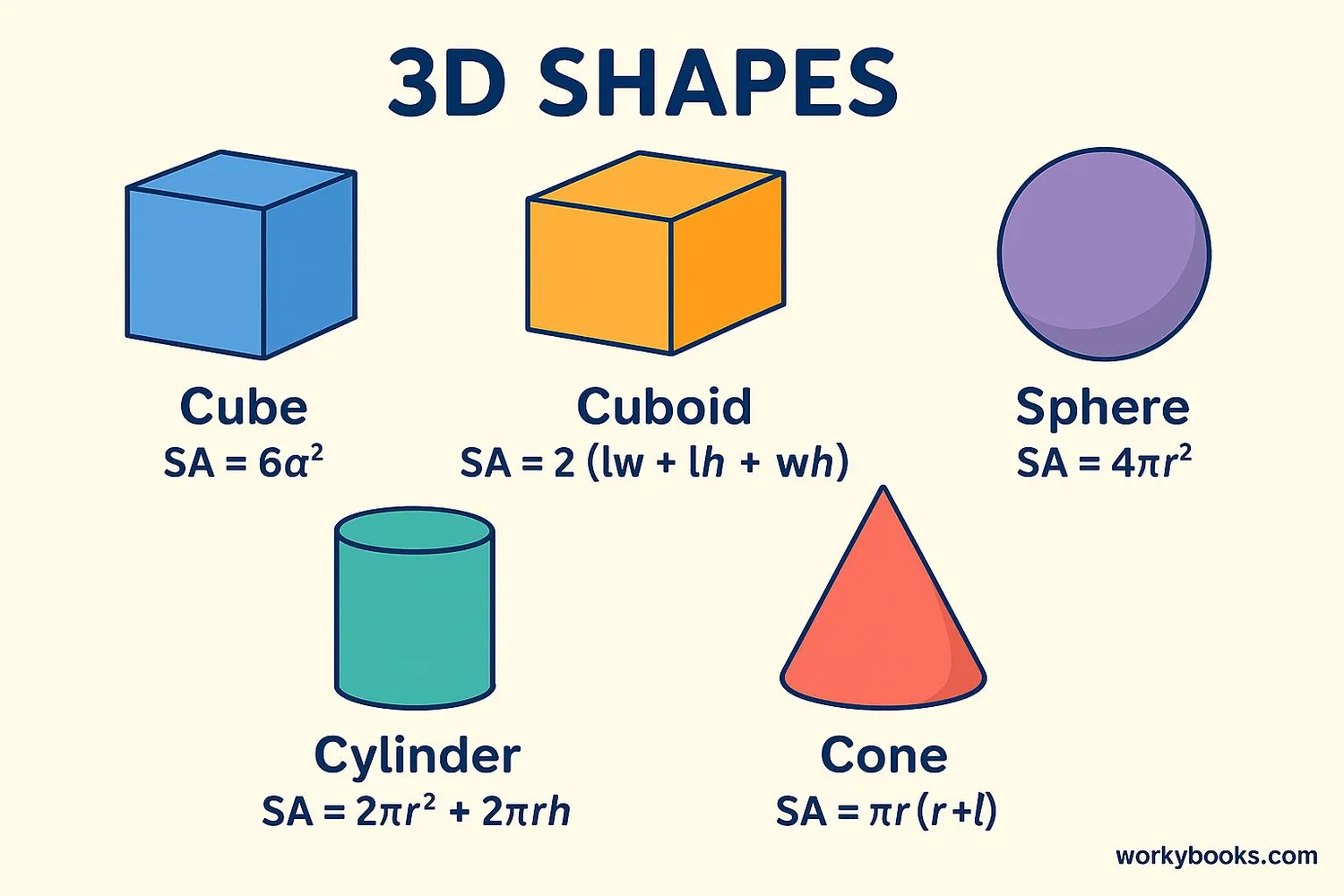
Different 3D shapes have different formulas for calculating their surface area. Here are the most common ones:
| Shape | Formula | Explanation |
|---|---|---|
| Cube | 6a² | 6 × (side × side) |
| Cuboid | 2(lw + lh + wh) | 2 × (length×width + length×height + width×height) |
| Cylinder | 2πr(h + r) | 2 × π × radius × (height + radius) |
| Cone | πr(r + l) | π × radius × (radius + slant height) |
| Sphere | 4πr² | 4 × π × radius² |
| Hemisphere | 3πr² | 3 × π × radius² |
Remember
Surface area is always measured in square units (cm², m², etc.) because it's a measure of area!
Types of Surface Area
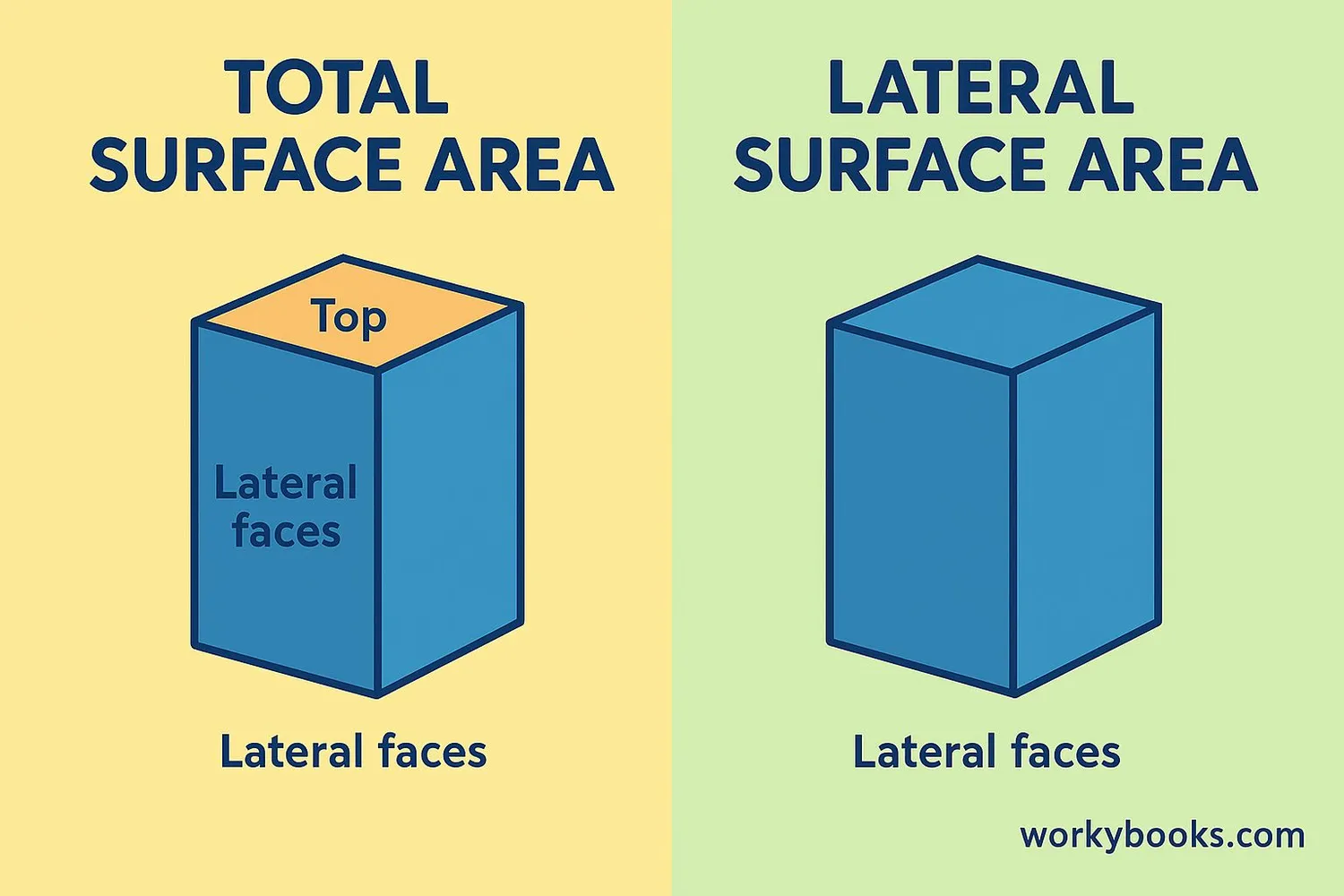
When working with 3D shapes, we sometimes calculate different types of surface area:
Total Surface Area (TSA)
The total surface area is the sum of all the surfaces of a 3D shape, including the top, bottom, and all sides.
For example, the TSA of a cube includes all six faces.
Lateral Surface Area (LSA)
The lateral surface area is the area of all the sides excluding the top and bottom.
For a cylinder, LSA is just the curved surface (2πrh), not including the circular ends.
Curved Surface Area (CSA)
The curved surface area is the area of only the curved parts of a shape.
For a cone, CSA is πrl (the conical part), not including the base.
Remember
Total Surface Area (TSA) = Lateral Surface Area (LSA) + Area of Bases
Surface Area of Cuboid & Cube
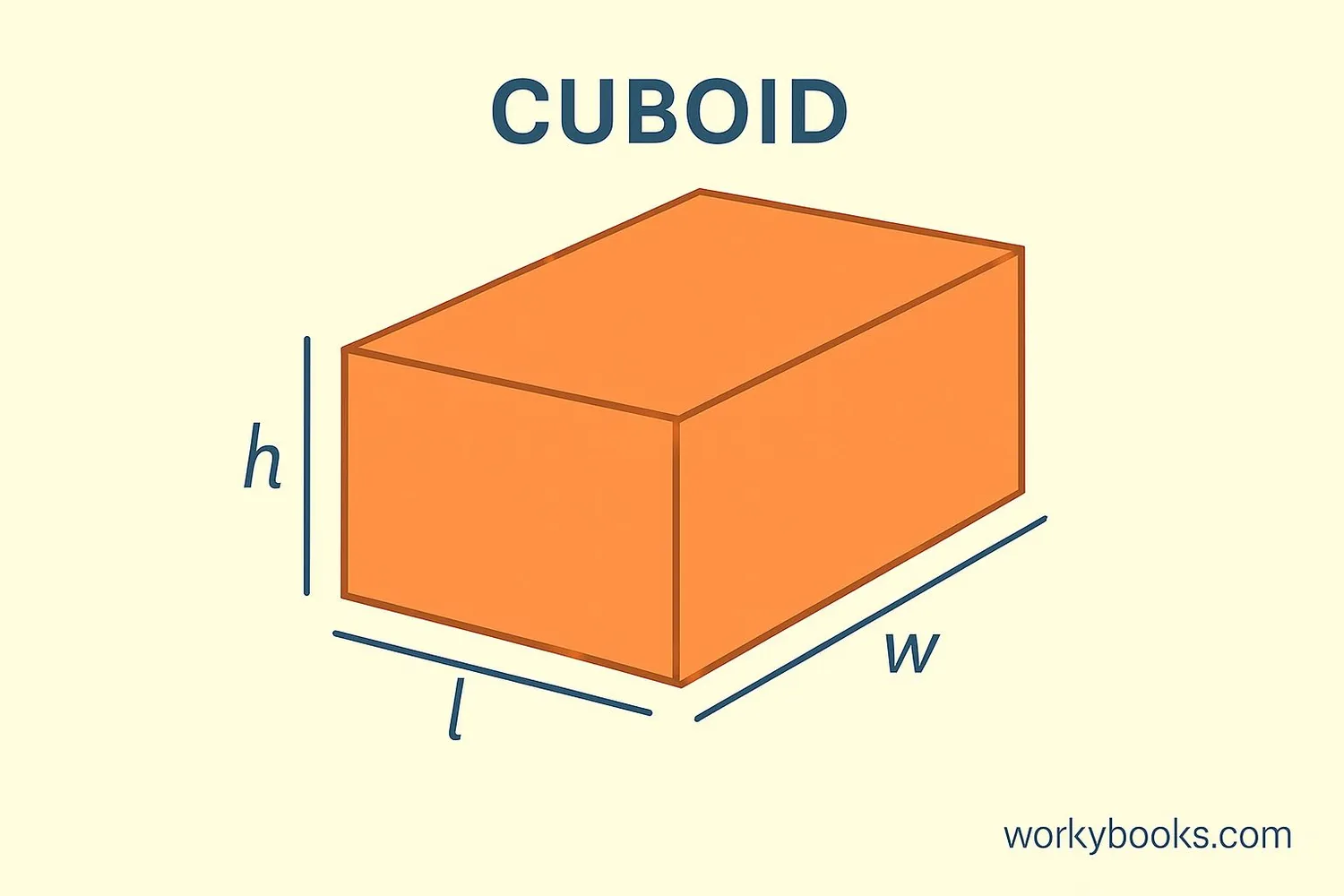
Cuboid: 2(lw + lh + wh)
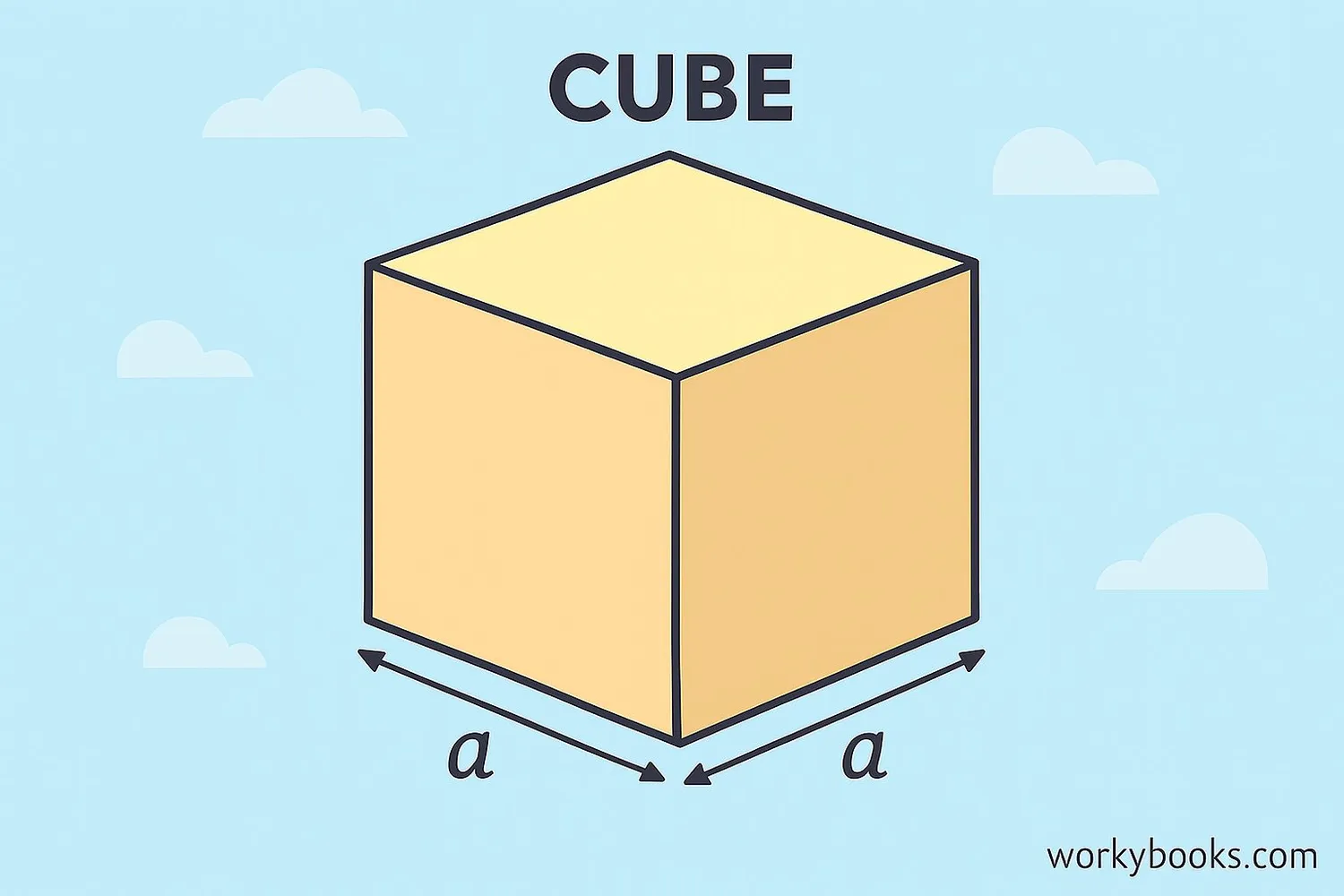
Cube: 6a²
Let's explore the surface area of rectangular prisms (cuboids) and cubes:
Cuboid (Rectangular Prism):
A cuboid has 6 rectangular faces. To find its surface area, we calculate the area of all 6 faces and add them together. Since opposite faces are equal, we can use the formula:
Where l = length, w = width, h = height
Solution: 2 × [(5×3) + (5×4) + (3×4)] = 2 × [15 + 20 + 12] = 2 × 47 = 94 cm²
Cube:
A cube is a special cuboid where all sides are equal. Since all 6 faces are identical squares, we can simplify the formula:
Where a = length of one side
Solution: 6 × (2 × 2) = 6 × 4 = 24 cm²
Surface Area of Cylinder
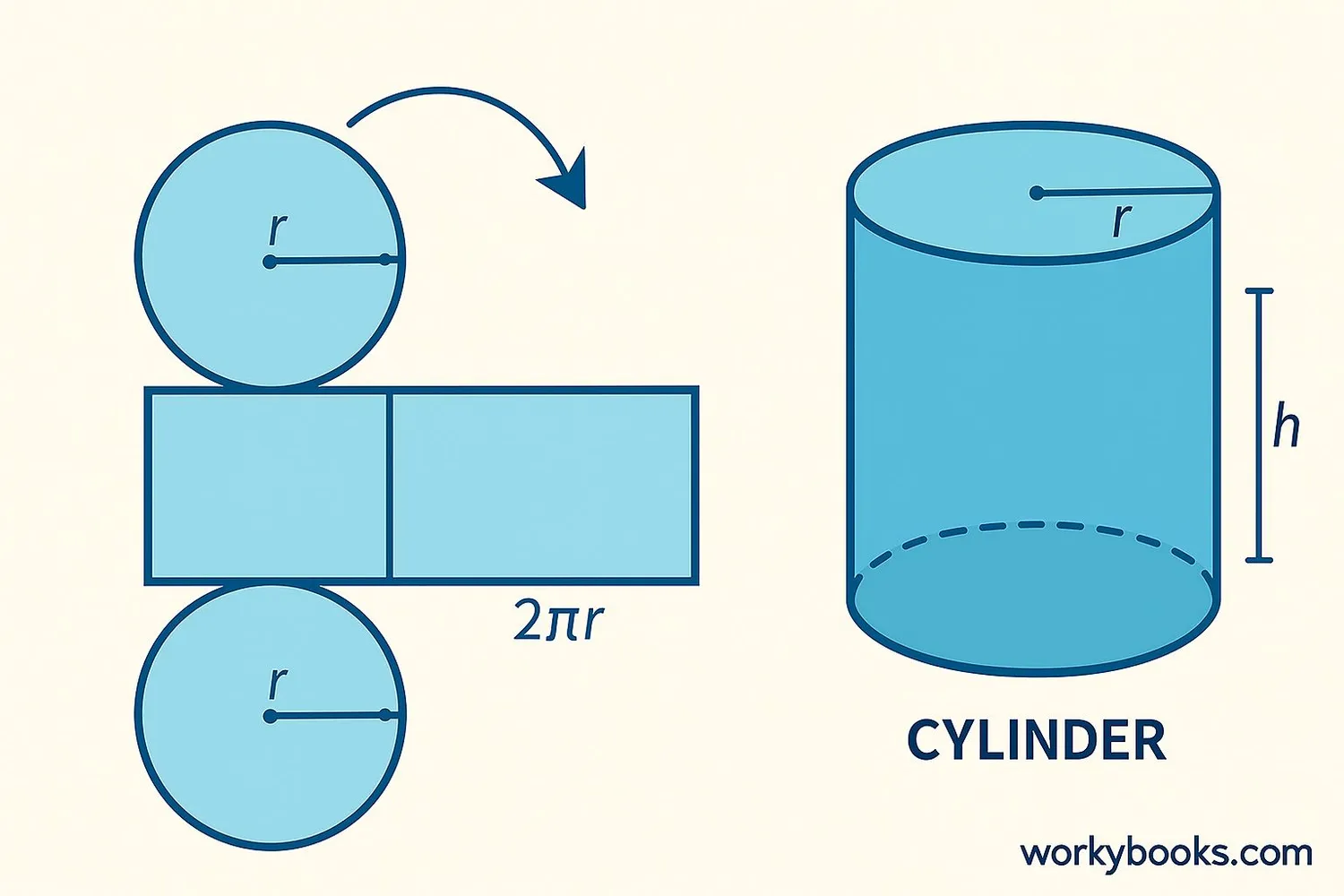
A cylinder has two circular bases and a curved surface. To find its total surface area:
Where r = radius, h = height
- Area of two circular bases: 2 × πr²
- Area of curved surface: 2πr × h
Solution: 2 × π × 3 × (5 + 3) = 6π × 8 = 48π ≈ 150.8 cm²
Lateral Surface Area:
Sometimes we only need the curved surface area (without the bases):
Surface Area of Cone & Sphere
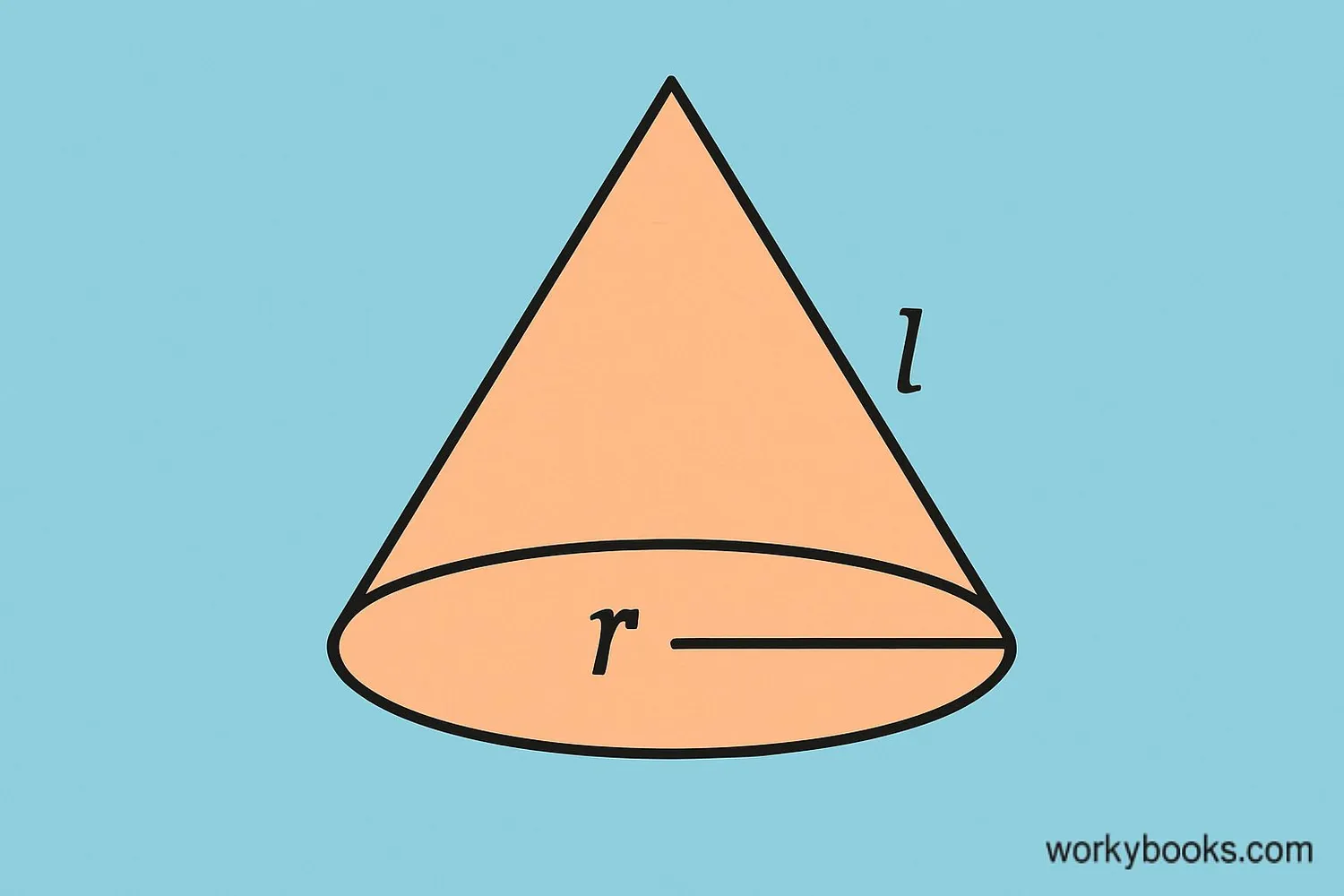
Cone: πr(r + l)

Sphere: 4πr²
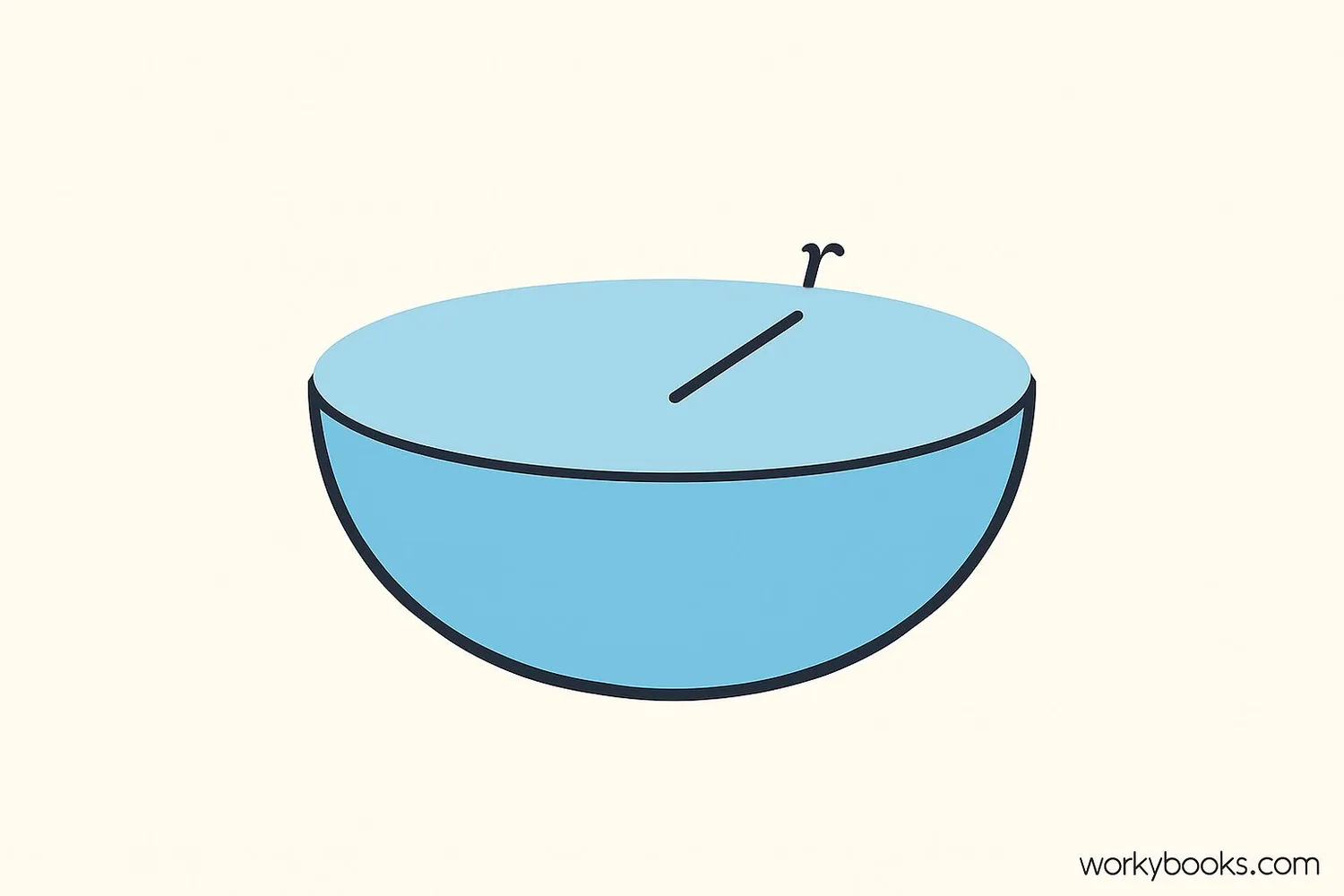
Hemisphere: 3πr²
Cone:
A cone has a circular base and a curved surface that tapers to a point (apex). The surface area formula is:
Where r = radius, l = slant height
Solution: π × 4 × (4 + 5) = 4π × 9 = 36π ≈ 113.1 cm²
Sphere:
A sphere is perfectly round, like a ball. Its surface area formula is:
Solution: 4 × π × (6)² = 4π × 36 = 144π ≈ 452.4 cm²
Hemisphere:
A hemisphere is half of a sphere plus the circular base:
Surface Area Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about surface area:
Geometry Trivia
Discover interesting facts about geometry and surface area:
Honeycomb Efficiency
Honeybees build hexagonal honeycombs because this shape provides the most storage space with the least amount of wax. The hexagon has a high volume-to-surface area ratio, making it very efficient!
Human Lungs
If you spread out all the tiny air sacs in human lungs, their total surface area would be about 70 square meters - roughly the size of a tennis court! This large surface area helps us absorb oxygen efficiently.
Planetary Surface Area
The surface area of Earth is approximately 510 million square kilometers. About 71% is covered by water. The largest planet in our solar system, Jupiter, has a surface area 120 times greater than Earth's!
The Menger Sponge
The Menger Sponge is a fractal with infinite surface area but zero volume! It's created by repeatedly dividing a cube into smaller cubes and removing some of them. This shows how surface area can behave strangely in mathematical shapes.





