Trinomial - Definition, Examples, Quiz, FAQ, Trivia

Learn about trinomials with easy explanations, examples, and interactive activities

Educational Standards

Common Core: A-SSE.A.2, A-SSE.B.3, A-APR.A.1

Learning Sections

What is a Trinomial? Types of Trinomials Factoring Trinomials Examples Practice Quiz FAQs Math Trivia

What is a Trinomial?

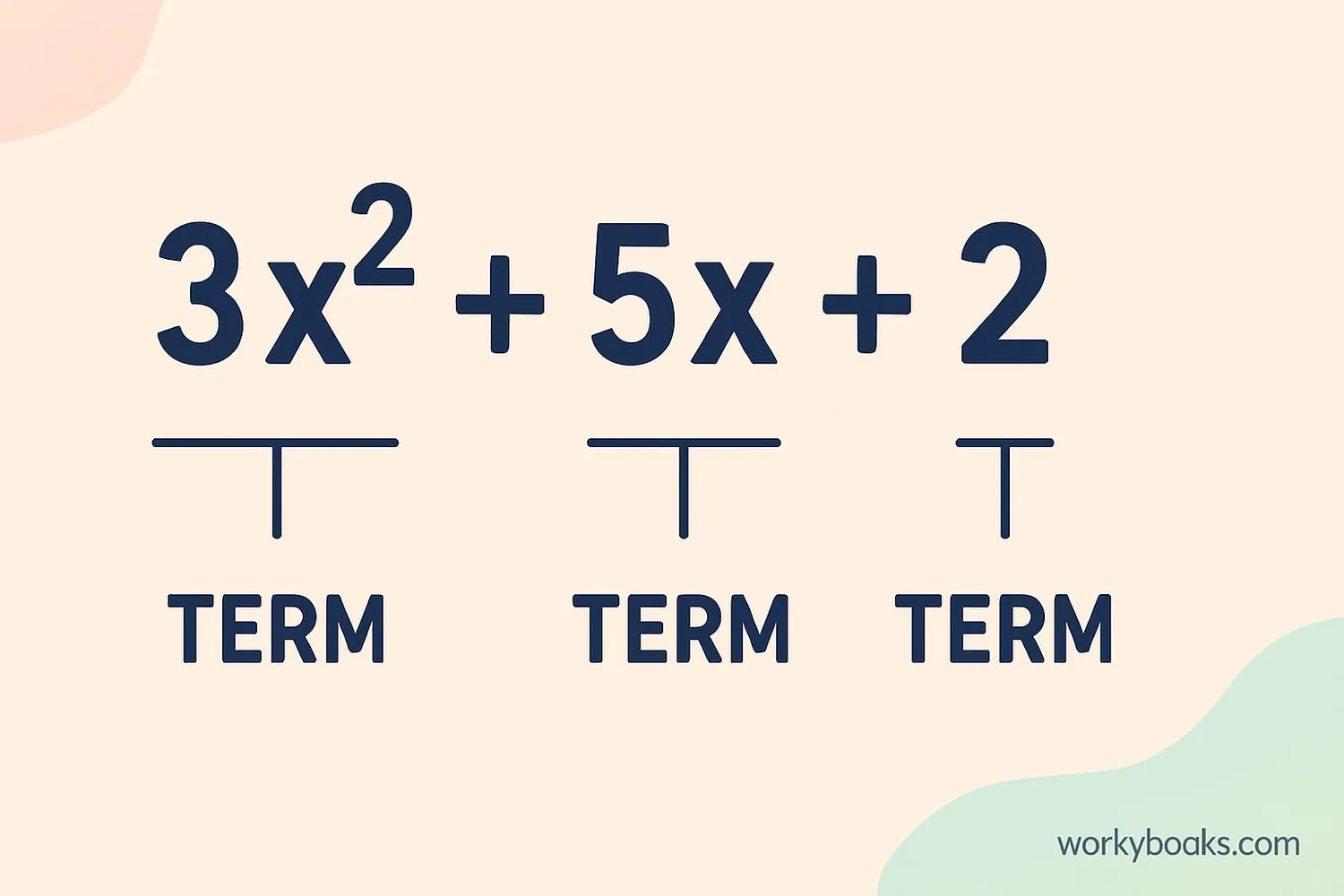
Visual representation of a trinomial expression

A trinomial is a special type of polynomial that has exactly three terms. Polynomials are expressions made up of variables and coefficients, combined using addition, subtraction, and multiplication.

The word "trinomial" comes from:

"Tri" meaning three
"Nomial" meaning terms

2x² + 5x - 3

This expression has three terms:

2x² (quadratic term)
5x (linear term)
-3 (constant term)

Trinomials are important in algebra because they appear in many mathematical situations, especially when we multiply two binomials together or when we factor quadratic expressions.

Key Concept

Trinomial = Three terms. Each term can have variables with exponents, coefficients, and constants.

Types of Trinomials

There are two important types of trinomials you should know:

1. Quadratic Trinomial

A quadratic trinomial has a degree of 2 (the highest exponent is 2). It looks like this:

ax² + bx + c

Where a, b, and c are numbers, and a ≠ 0.

Example: 3x² - 4x + 1

2. Perfect Square Trinomial

This special trinomial comes from squaring a binomial. It has the pattern:

a² + 2ab + b² = (a + b)²
a² - 2ab + b² = (a - b)²

Example: x² + 6x + 9 = (x + 3)²

Recognizing these types helps us solve equations and factor expressions more easily.

Factoring Trinomials

Factoring trinomials means breaking them down into simpler expressions that multiply to give the original trinomial. Here's how to factor quadratic trinomials:

Factoring Method

For a trinomial: ax² + bx + c

Find two numbers that:

1. Multiply to give a × c

2. Add to give b

Example: Factor x² + 5x + 6

a = 1, b = 5, c = 6
Find two numbers that multiply to 1×6 = 6 and add to 5
The numbers are 2 and 3 (because 2×3=6 and 2+3=5)
Write as: (x + 2)(x + 3)

For perfect square trinomials, we can use the formula:

a² + 2ab + b² = (a + b)²
a² - 2ab + b² = (a - b)²

Example: x² - 8x + 16 = (x - 4)²

Real-World Examples

Real-world applications of trinomials — Trinomials in everyday life

Trinomials appear in many real-world situations:

Example 1: Projectile Motion

The height of a ball thrown in the air can be modeled by a quadratic trinomial: h = -5t² + 20t + 1

Example 2: Area Calculations

The area of a rectangle with sides (x+3) and (x+5) is given by the trinomial: A = (x+3)(x+5) = x² + 8x + 15

Example 3: Business Profit

A company's profit might be modeled by: P = -2x² + 100x - 800, where x is the number of items sold

Example 4: Factoring Practice

Factor the trinomial: 2x² + 7x + 3

Solution:

a = 2, b = 7, c = 3
Find numbers that multiply to 2×3=6 and add to 7: 6 and 1
Rewrite: 2x² + 6x + x + 3
Group: (2x² + 6x) + (x + 3)
Factor: 2x(x + 3) + 1(x + 3)
Result: (2x + 1)(x + 3)

Trinomial Quiz

Test your knowledge with this 5-question quiz. Choose the correct answer for each question.

1. How many terms does a trinomial have?

One

Two

Three

Four

2. Which of these is a quadratic trinomial?

3x + 2

x² - 4x + 4

5x³ - 2x² + x - 1

2x - 7

3. What is the factored form of x² + 7x + 12?

(x + 2)(x + 6)

(x + 3)(x + 4)

(x + 1)(x + 12)

(x + 5)(x + 7)

4. Which trinomial is a perfect square?

x² + 3x + 2

x² - 6x + 9

x² + 5x + 10

x² - 2x - 3

5. What numbers multiply to 12 and add to 7?

2 and 6

3 and 4

1 and 12

5 and 7

Math Master! You've shown excellent understanding of trinomials!

Good effort! Review the concepts and try again.

Frequently Asked Questions

Here are answers to common questions about trinomials:

What's the difference between binomial and trinomial?

A binomial has two terms (like 2x + 3), while a trinomial has three terms (like x² + 4x + 4). Both are types of polynomials, but they have different numbers of terms.

Why is factoring trinomials important?

Factoring helps us solve equations, simplify expressions, and find important values like maximums and minimums in real-world problems. It's a fundamental skill in algebra that prepares you for more advanced math.

Can all trinomials be factored?

Not all trinomials can be factored using real numbers. Some trinomials are "prime" and cannot be broken down further. However, most trinomials you'll encounter in basic algebra can be factored.

How do I know if a trinomial is a perfect square?

A perfect square trinomial takes the form a² ± 2ab + b². The first and last terms must be perfect squares, and the middle term must be twice the product of the square roots of the first and last terms.

Math Trivia

Discover interesting facts about algebra and polynomials:

Ancient Algebra

The word "algebra" comes from the Arabic word "al-jabr", which means "reunion of broken parts". It was first used by mathematician Muhammad ibn Musa al-Khwarizmi in the 9th century.

Polynomial Power

The longest polynomial ever used in a mathematical proof had more than 1,000 terms! Most polynomials we use in everyday math have just a few terms.

Algebra in Space

NASA engineers use polynomial equations to calculate rocket trajectories. Quadratic equations (which come from trinomials) help determine the path of spacecraft!

Polynomial Records

The largest degree polynomial ever solved was of degree 1,000, but this required supercomputers. Most classroom polynomials have degrees between 2 and 4.

Related Resources

No resources found matching the criteria.