Undefined - Definition, Examples, Quiz, FAQ, Trivia
Learn about mathematical expressions that don't have answers and why they matter
What Does "Undefined" Mean in Math?

In mathematics, "undefined" means that an expression doesn't have a meaningful answer. It's like asking a question that can't be answered, such as "What color is Tuesday?" Some things just don't make sense in math, and that's when we say they're undefined.
For example, if you try to divide a number by zero, like 5 ÷ 0, there's no possible answer. We say this expression is undefined. It's not that we don't know the answer - it's that there is no answer!
Understanding undefined expressions helps us avoid mistakes in math and shows us the boundaries of what numbers can do.
Key Concept
Undefined means "no answer possible" - not that we don't know the answer yet.
Common Undefined Expressions
Let's look at some common expressions that are undefined in mathematics:
1. Division by zero: Any number divided by zero is undefined. Why? Because division means "how many times does this number fit into that number?" Nothing can fit into a number zero times! 5 ÷ 0 has no meaning.
2. Square roots of negative numbers: In basic math, the square root of a negative number is undefined. Why? Because no real number multiplied by itself gives a negative result. √(-4) is undefined in real numbers.
3. Zero to the power of zero: 0⁰ is undefined because mathematicians can't agree on what it should be. Some say 1, others say 0, so we leave it undefined.
Undefined Expressions
Remember
Computers show "NaN" (Not a Number) when they encounter undefined expressions!
Undefined Terms in Geometry
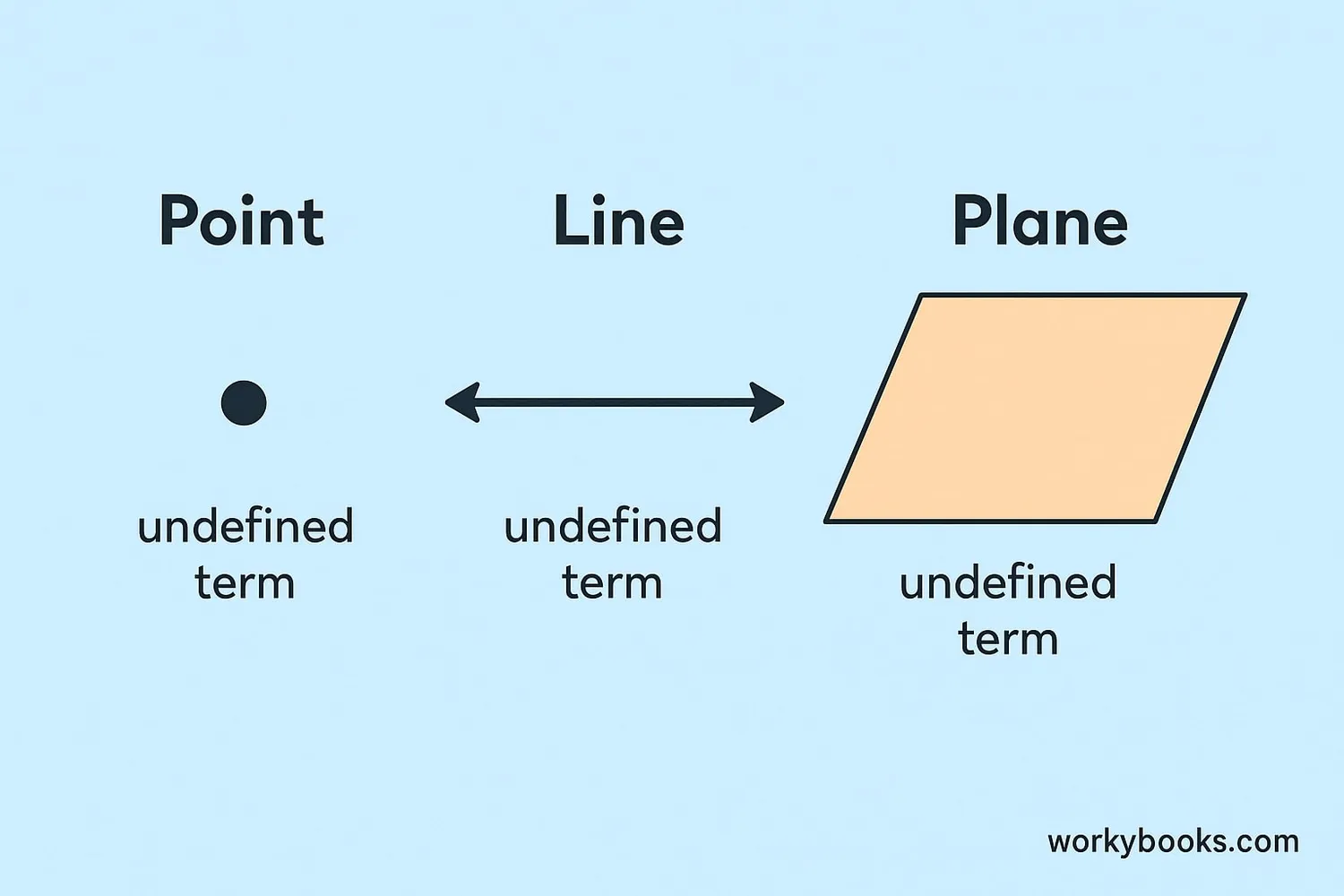
In geometry, we have some special "undefined terms" that we use to define everything else. These are:
Point: A location in space with no size. We represent it with a dot, but it has no dimensions. We can't define it with simpler ideas.
Line: A straight path that goes on forever in both directions. It has no thickness. We understand lines through examples, but can't define them with simpler terms.
Plane: A flat surface that extends forever in all directions. Think of it like an endless sheet of paper.
These undefined terms are the building blocks of geometry. We use them to define other concepts like angles, triangles, and circles.
Geometry Tip
We start with undefined terms to avoid circular definitions. Everything else is defined using these basic ideas!
Why Understanding Undefined Matters

Understanding undefined expressions is important for several reasons:
1. Avoiding mistakes: If we try to use undefined expressions in calculations, we get wrong answers. Recognizing them helps us avoid these mistakes.
2. Computer programming: Computers need to know when an operation is undefined so they can show an error instead of giving a wrong answer.
3. Advanced mathematics: As you learn more math, you'll discover that some undefined expressions in basic math have special meanings in advanced topics (like imaginary numbers for √(-1)).
4. Critical thinking: Understanding why some things are undefined helps develop logical thinking skills.
Real-World Connection
In 1997, a US Navy ship crashed because a computer tried to divide by zero!
Undefined Expressions Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about undefined in mathematics:
Math Trivia
Discover interesting facts about undefined concepts in mathematics:
Ancient Zero Problem
The concept of zero and division by zero puzzled ancient mathematicians. Indian mathematician Brahmagupta was one of the first to discuss division by zero around 628 AD.
Computer Errors
In 1997, the USS Yorktown cruiser was dead in the water for 2 hours 45 minutes because a crew member entered a zero into a database field, causing a division by zero error.
Imaginary Numbers
While √(-1) is undefined in real numbers, mathematicians created imaginary numbers (i) to solve this problem. These are essential in engineering and physics today!
Pointless Geometry
Euclid's Elements (300 BC) begins with definitions of point, line, and plane as the foundation of geometry - but never actually defines them! They're primitive notions.





