Uniform Distribution - Definition, Examples, Quiz, FAQ, Trivia
Learn about equal chances in probability with fun examples and activities
What is Uniform Distribution?

Uniform distribution is a special kind of probability where every outcome has an equal chance of happening.
It's like rolling a fair die - each number from 1 to 6 has exactly the same probability of landing face up.
Think of it as a perfectly fair game where nobody has an advantage. Whether you're flipping a coin, spinning a spinner with equal sections, or drawing a card from a well-shuffled deck, if all outcomes are equally likely, you're looking at uniform distribution!
The word "uniform" means "the same in all cases" - so in uniform distribution, every possibility has exactly the same chance of occurring.
Key Concept
In uniform distribution, all outcomes have equal probability. For example, with a fair 6-sided die, each number has a 1/6 chance.
Types of Uniform Distribution
There are two main types of uniform distribution:
1. Discrete Uniform Distribution: This is for things you can count with separate possibilities. Examples include:
- Rolling a die (1, 2, 3, 4, 5, or 6)
- Flipping a coin (heads or tails)
- Drawing a card from a deck (52 possibilities)
- The exact time a bus arrives between 3:00 and 3:10
- A random point selected on a 10cm ruler
- The temperature at a random moment during a day with constant temperature
Remember
Discrete = separate possibilities (like whole numbers), Continuous = any value in a range (like decimals).
Formula & Properties
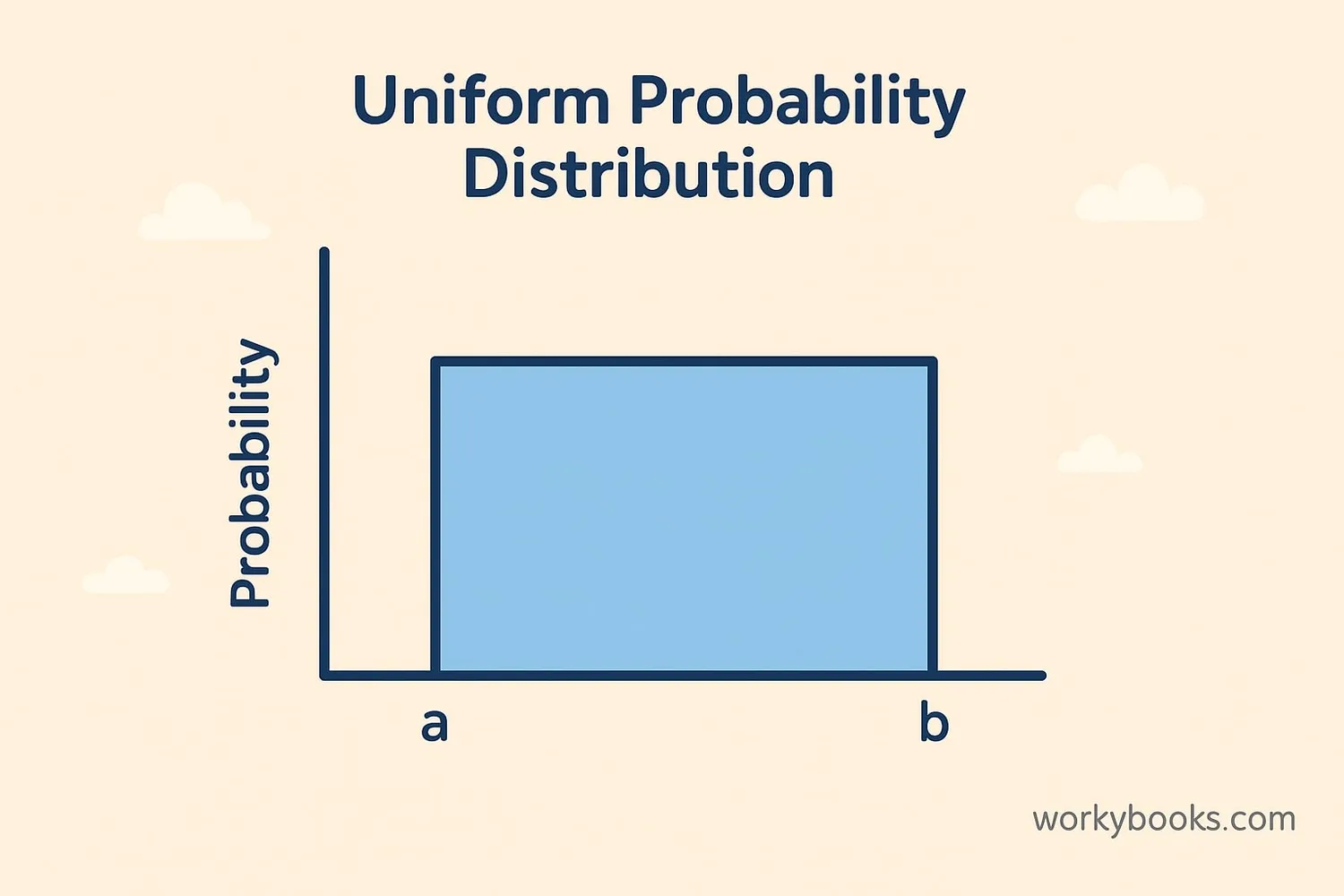
The uniform distribution has some special mathematical properties that make it easy to work with:
Probability Formula
For a fair 6-sided die, the probability of any number is 1/6 ≈ 0.1667
- Flat Shape: The graph of uniform distribution is flat and rectangular, which is why it's sometimes called "rectangular distribution"
- Equal Height: All probabilities are the same height on the graph
- Mean: The average is exactly in the middle of the range
- Variance: This measures how spread out the values are
- Probability Density = 1/(b-a)
- Mean = (a+b)/2
- Variance = (b-a)²/12
Math Tip
To find the probability of an event with uniform distribution, just count the possibilities you want and divide by the total possibilities!
Real-World Examples

Uniform distribution appears in many everyday situations:
Example 1: Rolling a Die
A fair 6-sided die has equal probability for each number (1/6). This is discrete uniform distribution.
Example 2: Flipping a Coin
A fair coin has two equally likely outcomes: heads (1/2) or tails (1/2).
Example 3: Drawing Cards
In a well-shuffled deck, each card has a 1/52 chance of being drawn.
Example 4: Random Number Generator
Computer programs that generate random numbers between 1 and 100 use continuous uniform distribution - each number has equal probability.
Example 5: Spinner with Equal Sections
If a spinner has 8 equal-sized sections, each color has a 1/8 probability of being selected.
Real-World Connection
Lottery drawings and bingo games often use uniform distribution to ensure every number has an equal chance!
Uniform Distribution Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about uniform distribution:
Probability Trivia
Discover interesting facts about probability and uniform distribution:
Ancient Dice
The oldest known dice date back over 5,000 years to ancient Mesopotamia. Early dice were made from animal bones, stones, and pottery.
Coin Flip Odds
In reality, coin flips aren't perfectly uniform! Research shows a coin has about a 51% chance of landing on the same side it started on.
Random Numbers in Space
NASA uses uniform distribution to generate random numbers for space missions, ensuring all possibilities have equal chance in calculations.
Largest Dice Collection
The world record for the largest collection of dice is held by Kevin Cook from the USA, with over 21,000 different dice!





