Vector - Definition, Examples, Quiz, FAQ, Trivia
Learn about direction and magnitude with simple explanations and fun activities
What are Vectors?
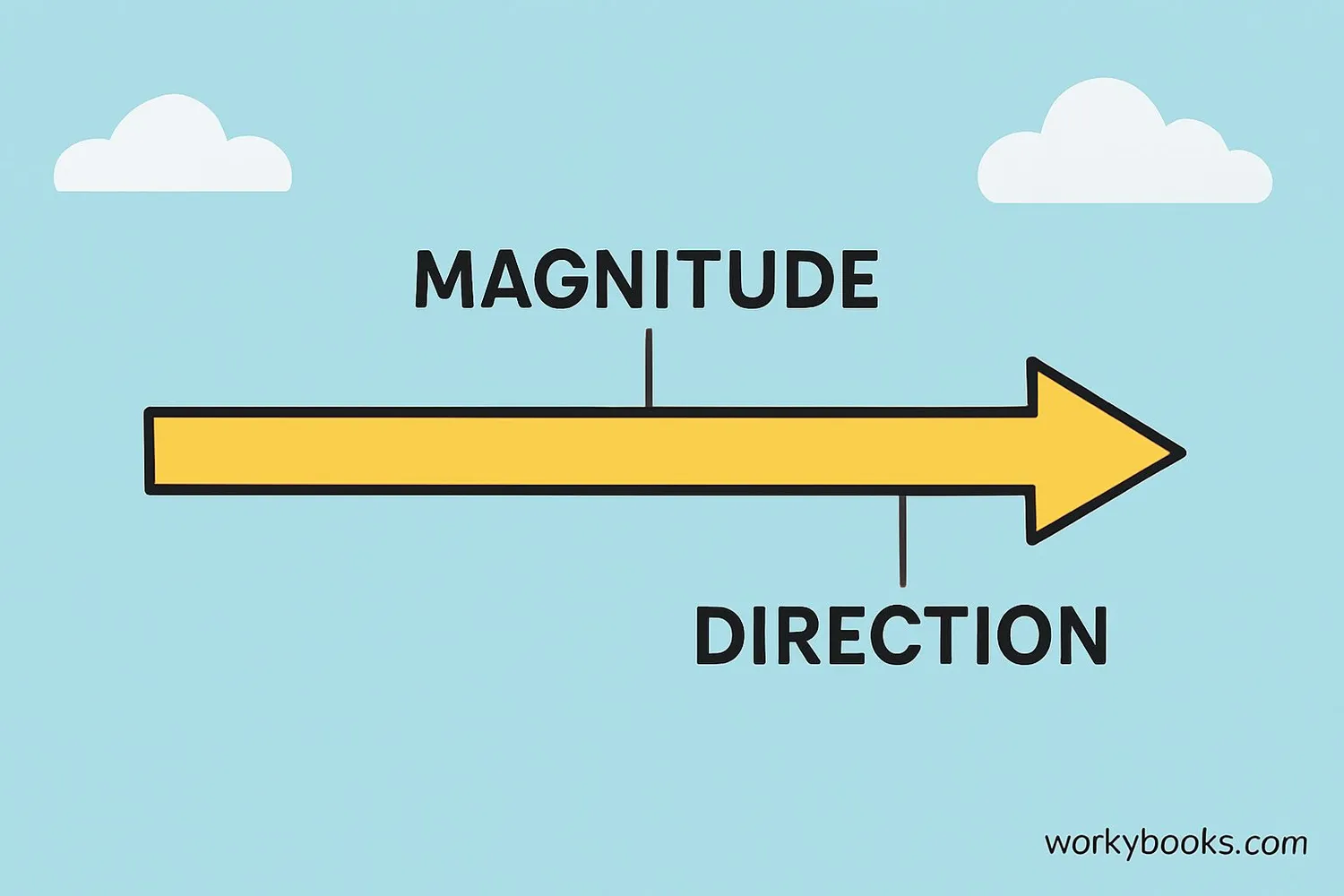
A vector is a mathematical object that has both magnitude (size) and direction. Think of it like an arrow - the length of the arrow shows how big it is, and where the arrow points shows its direction.
Vectors are different from regular numbers (called scalars) because scalars only have size. For example, temperature is a scalar (just a number), but wind velocity is a vector (it has speed and direction).
We use vectors to describe things that have both size and direction, such as:
- Displacement (how far you move and in what direction)
- Velocity (how fast you're going and where)
- Force (how strong a push or pull is and where it's applied)
Key Concept
All vectors have two important features: magnitude (how much) and direction (which way).
Types of Vectors
Zero Vector
A vector with zero magnitude. It has no direction and is represented as a point.
Unit Vector
A vector with magnitude of 1. It shows direction only.
Position Vector
Shows the position of a point relative to an origin.
Co-initial Vectors
Vectors that start from the same point.
Vectors can be classified in different ways based on their properties:
Like and Unlike Vectors: Vectors with the same direction are called like vectors, while those with opposite directions are unlike vectors.
Co-planar Vectors: Vectors that lie on the same plane (like on a flat sheet of paper).
Equal Vectors: Vectors that have the same magnitude and direction, regardless of their starting points.
Remember
The most important vectors for beginners are position vectors, unit vectors, and equal vectors.
Vector Operations
We can perform mathematical operations with vectors:
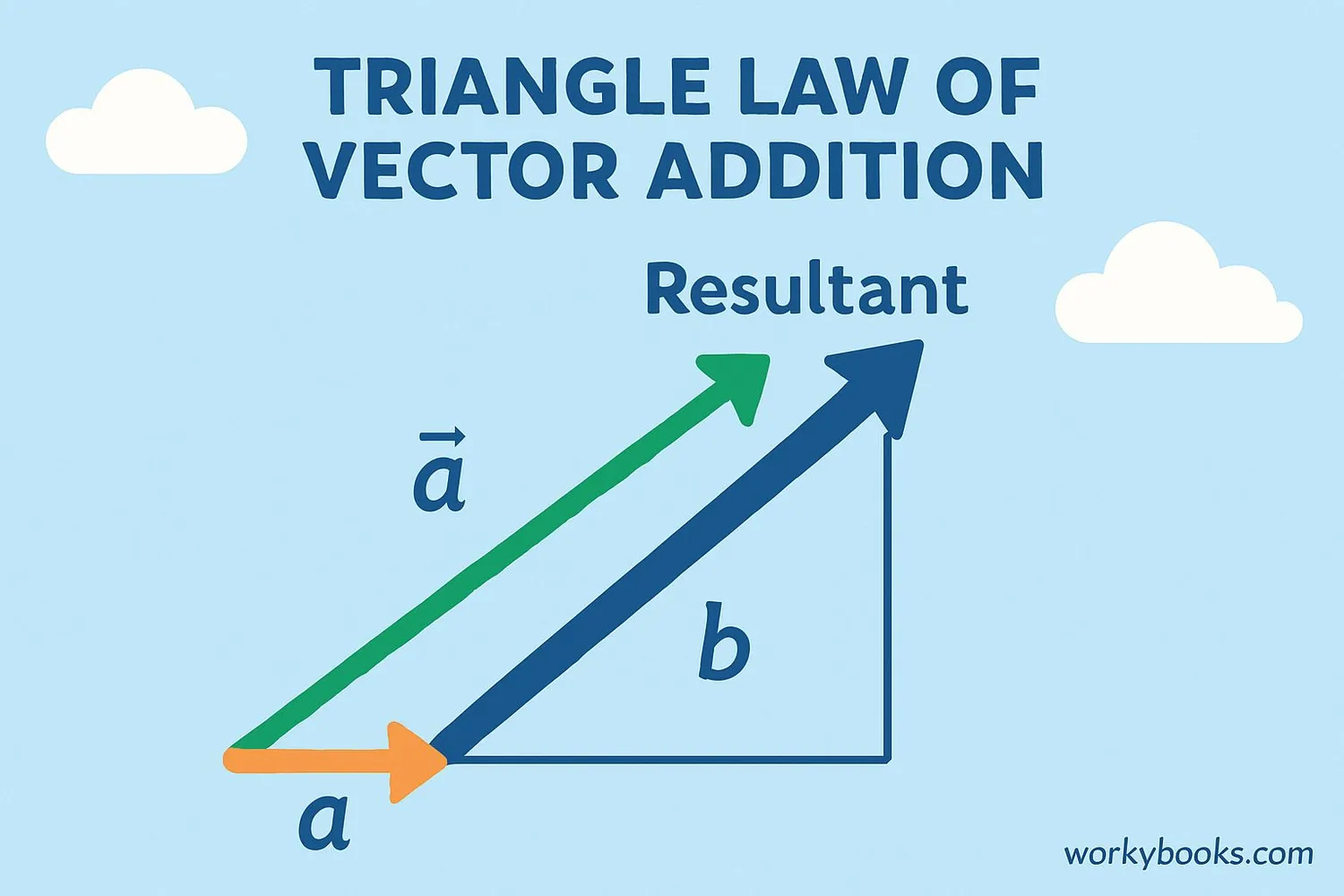
Vector Addition: When we add two vectors, we get a new vector called the resultant. There are two main ways to add vectors:
- Triangle Law: Place the tail of the second vector at the head of the first. The resultant goes from the tail of the first to the head of the second.
- Parallelogram Law: When vectors start from the same point, draw a parallelogram. The diagonal is the resultant.
Scalar Multiplication: When we multiply a vector by a regular number (scalar), we change its magnitude but not its direction (unless the scalar is negative, which reverses direction).
Vector Addition Formula
The resultant vector R is the sum of vectors A and B
Real-world Examples

Vectors are all around us in everyday life:
Navigation: When a plane flies, its velocity is a vector - it has speed (magnitude) and direction (where it's heading).
Sports: When you kick a soccer ball, the force you apply is a vector - it has strength (how hard you kick) and direction (where you aim).
Weather: Wind is described using vectors - wind speed (magnitude) and wind direction.
Video Games: Characters' movements are controlled using vectors - the direction they move and how fast.
Engineering: When building bridges, engineers calculate all the force vectors to make sure the bridge is strong enough.
Try This
Draw vectors showing your movement from your desk to the classroom door. What direction? How many steps? That's displacement!
Vector Quiz
Test your knowledge about vectors with this fun quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about vectors:
Vector Trivia
Discover fascinating facts about vectors:
Ancient Origins
The concept of vectors dates back to the 1600s, but the term "vector" was first used by Irish mathematician William Rowan Hamilton in 1846.
DNA Vectors
In biology, scientists use "vectors" to deliver genetic material into cells - like molecular delivery trucks! This is different from math vectors but uses the same idea of direction.
Space Navigation
NASA uses vectors to plan spacecraft trajectories. Getting to the Moon requires calculating many vectors to account for Earth's rotation, gravity, and the Moon's motion.
Vector Superheroes
Superheroes like The Flash use vector concepts when they run - their velocity vectors determine how fast they go and in what direction. Even superheroes need math!





