Vertex - Definition, Examples, Quiz, FAQ, Trivia
Learn about corners of shapes and connections in graphs with easy explanations and practice activities
What is a Vertex?
A vertex (plural: vertices) is a special point where two or more lines meet to form a corner. Think of it as the "elbow" of a shape where two sides come together.
Vertices are important in both geometry and graph theory:
- In geometry, vertices are the corners of shapes like triangles, squares, and pyramids.
- In graph theory, vertices are points that connect to other points with edges.
The word "vertex" comes from Latin and means "highest point." In math, it doesn't always mean the top point - it can be any corner of a shape!
Key Concept
A vertex is a point where two or more lines, edges, or curves meet.
Vertices in Geometry
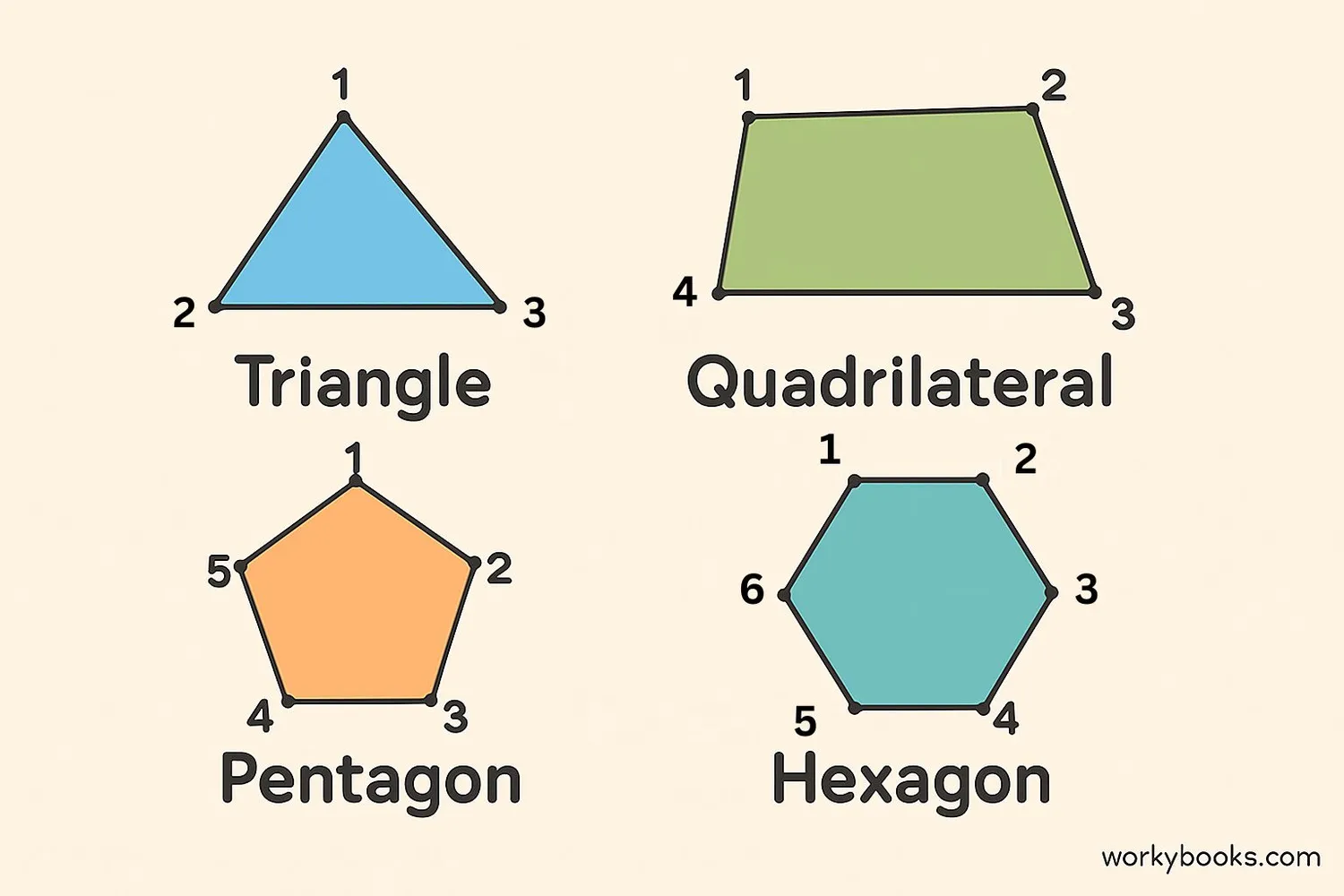
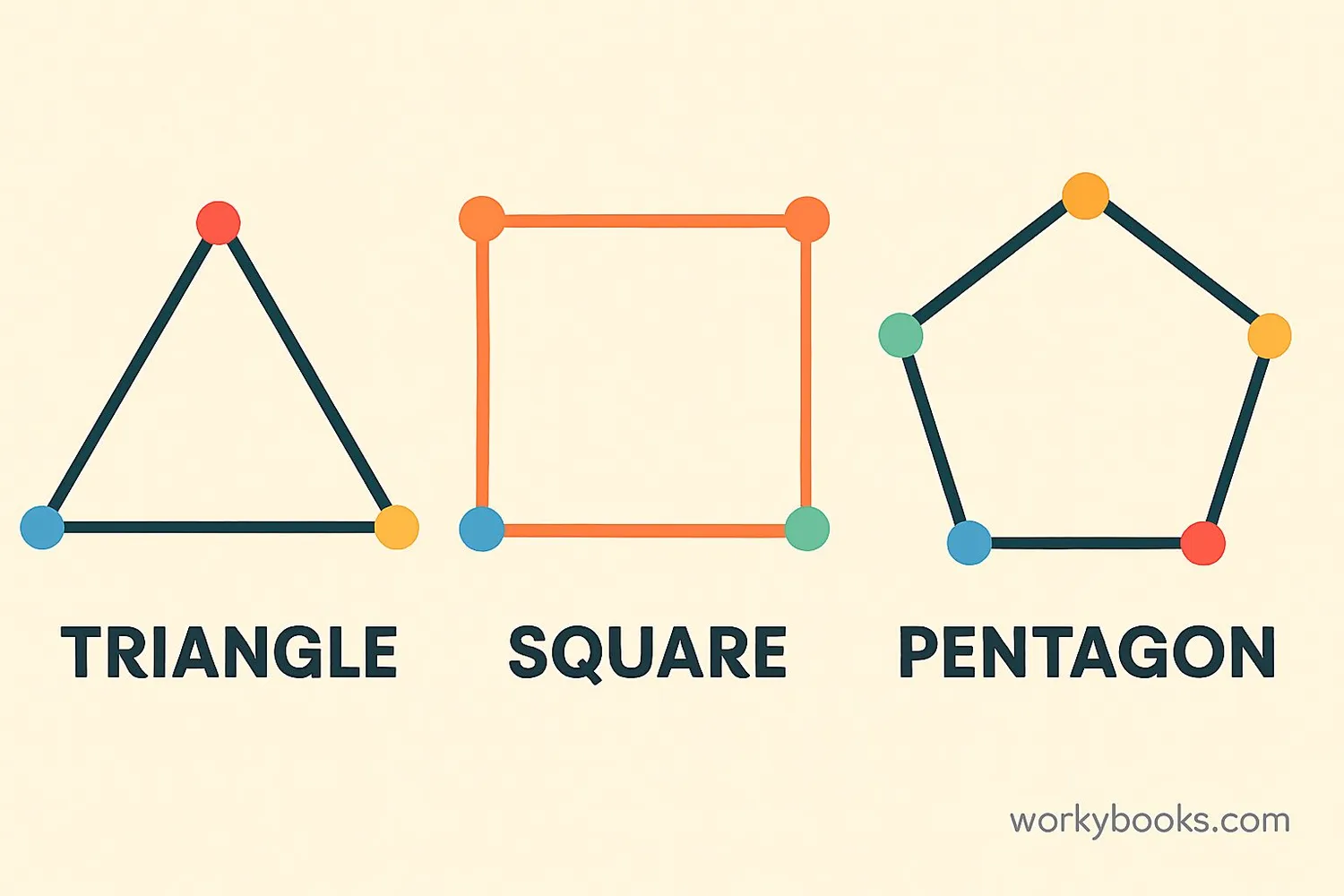
In geometry, a vertex is where two or more sides of a shape meet. Let's see how vertices work in different shapes:
Triangle
3 vertices
Square
4 vertices
Pentagon
5 vertices
Octagon
8 vertices
3D shapes have vertices too! A cube has 8 vertices, while a pyramid might have 4 or 5 vertices. Vertices help us describe and understand shapes in our world.
Remember
The number of vertices a shape has tells us what kind of polygon it is. More vertices mean more sides!
Vertices in Graphs
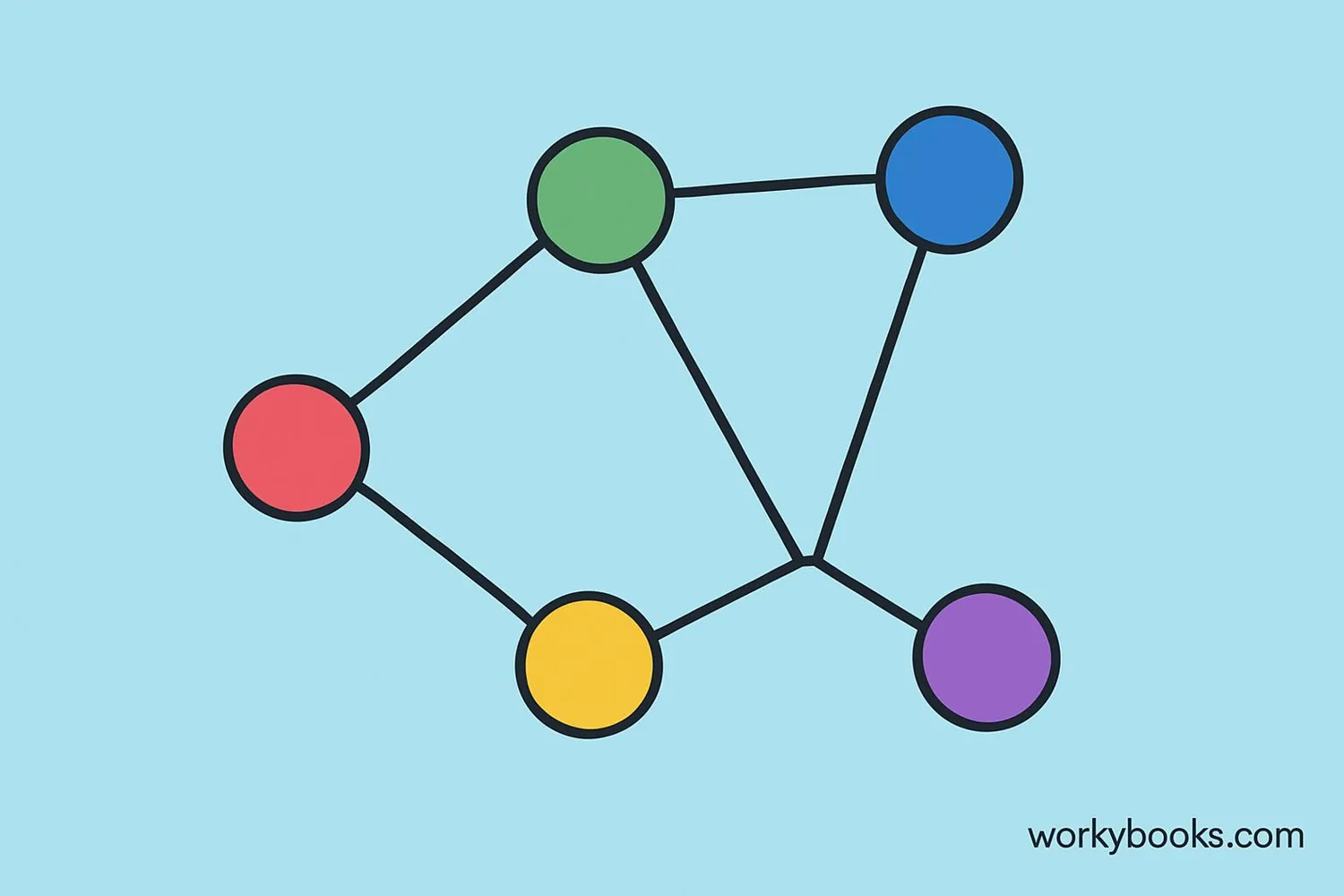
In graph theory (which is different from bar graphs or charts), a vertex is a fundamental unit. Here, vertices are connected by lines called edges.
Think of vertices as:
- Bus stops on a map
- People in a social network
- Computers on the internet
Each vertex can connect to other vertices with edges. The number of connections a vertex has is called its degree.
Important graph concepts:
Vertex cover: A set of vertices that "cover" all edges
Feedback vertex set: Vertices that remove all cycles
Convexity: Vertices that form outward-pointing corners
Graph Tip
In a graph, a vertex with many connections is called a "hub" - like a popular person with many friends!
Real-World Examples
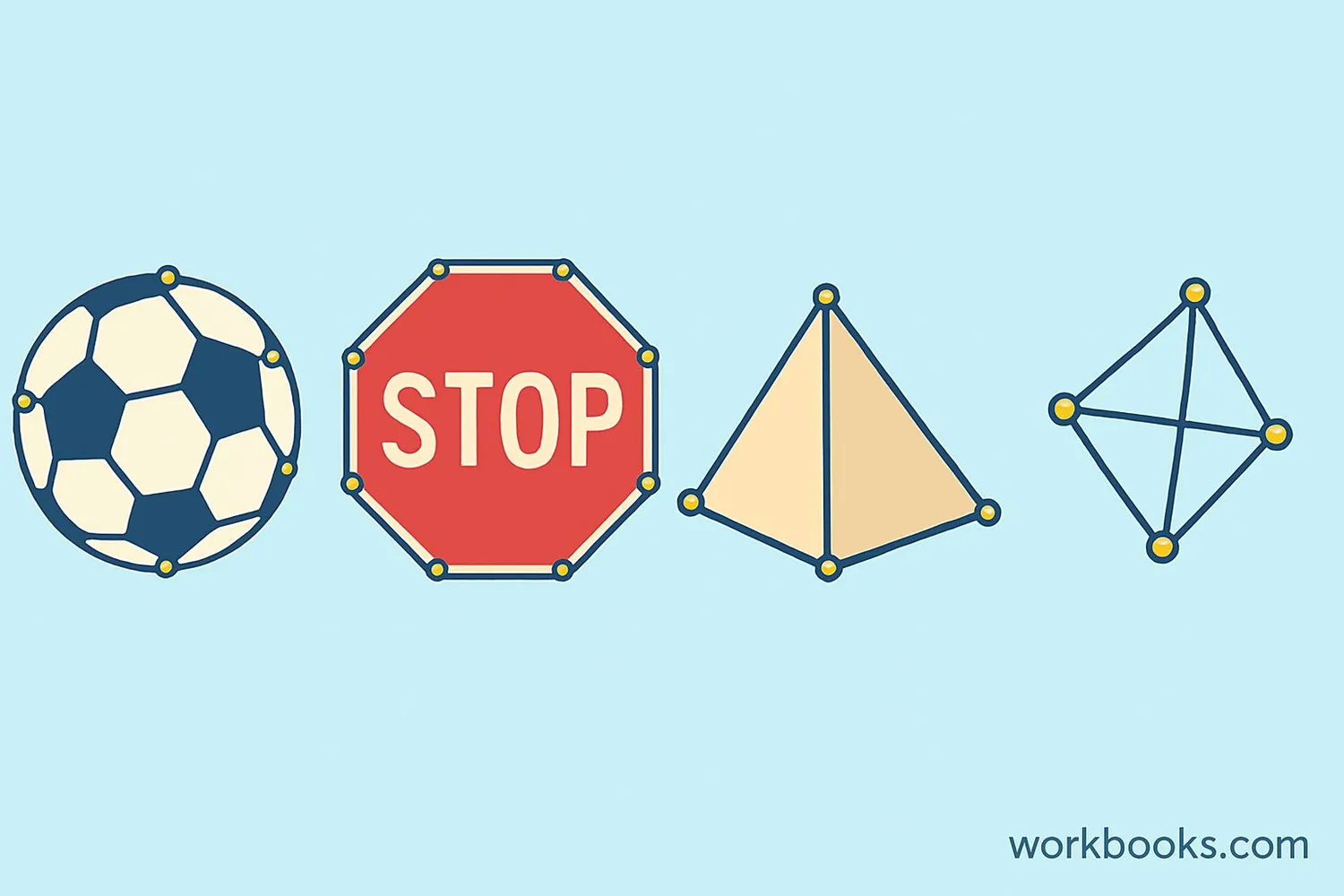
Vertices are all around us! Here are some real-world examples:
Example 1: A soccer ball has vertices where the pentagons and hexagons meet. A standard soccer ball has 60 vertices!
Example 2: A stop sign is an octagon with 8 vertices. Each corner is a vertex.
Example 3: In a city map, each intersection can be considered a vertex, while the roads are edges connecting them.
Example 4: When you play connect-the-dots, each dot is a vertex, and the lines you draw are edges.
Example 5: In a computer network, each device (computer, printer, router) is a vertex, and the connections between them are edges.
Try This
Look around your classroom - how many vertices can you find on different objects? Count the vertices on a book, a window, or your desk!
Vertex Knowledge Quiz
Test what you've learned with this 5-question quiz. Choose the best answer for each question.
Frequently Asked Questions
Here are answers to common questions about vertices:
Math Trivia
Discover interesting facts about vertices and math:
Ancient Geometry
The ancient Greeks were the first to systematically study vertices around 300 BCE. Euclid's "Elements" described geometric shapes using vertices over 2,000 years ago!
Molecular Vertices
In chemistry, molecules like water (H₂O) form a vertex where the oxygen atom sits, with hydrogen atoms at the ends. The angle at this vertex determines the molecule's properties.
GPS Technology
GPS navigation systems use graph theory with vertices representing locations and edges representing roads. Finding the shortest path between vertices helps you get where you're going!
The Most Vertices
The rhombicosidodecahedron is an Archimedean solid with 60 vertices! It has 20 triangular faces, 30 square faces, and 12 pentagonal faces.





