Vertical Angles - Definition, Examples, Facts & Quiz, FAQ, Trivia
Learn about opposite angles in geometry with simple explanations, visual examples, and practice activities
What Are Vertical Angles?
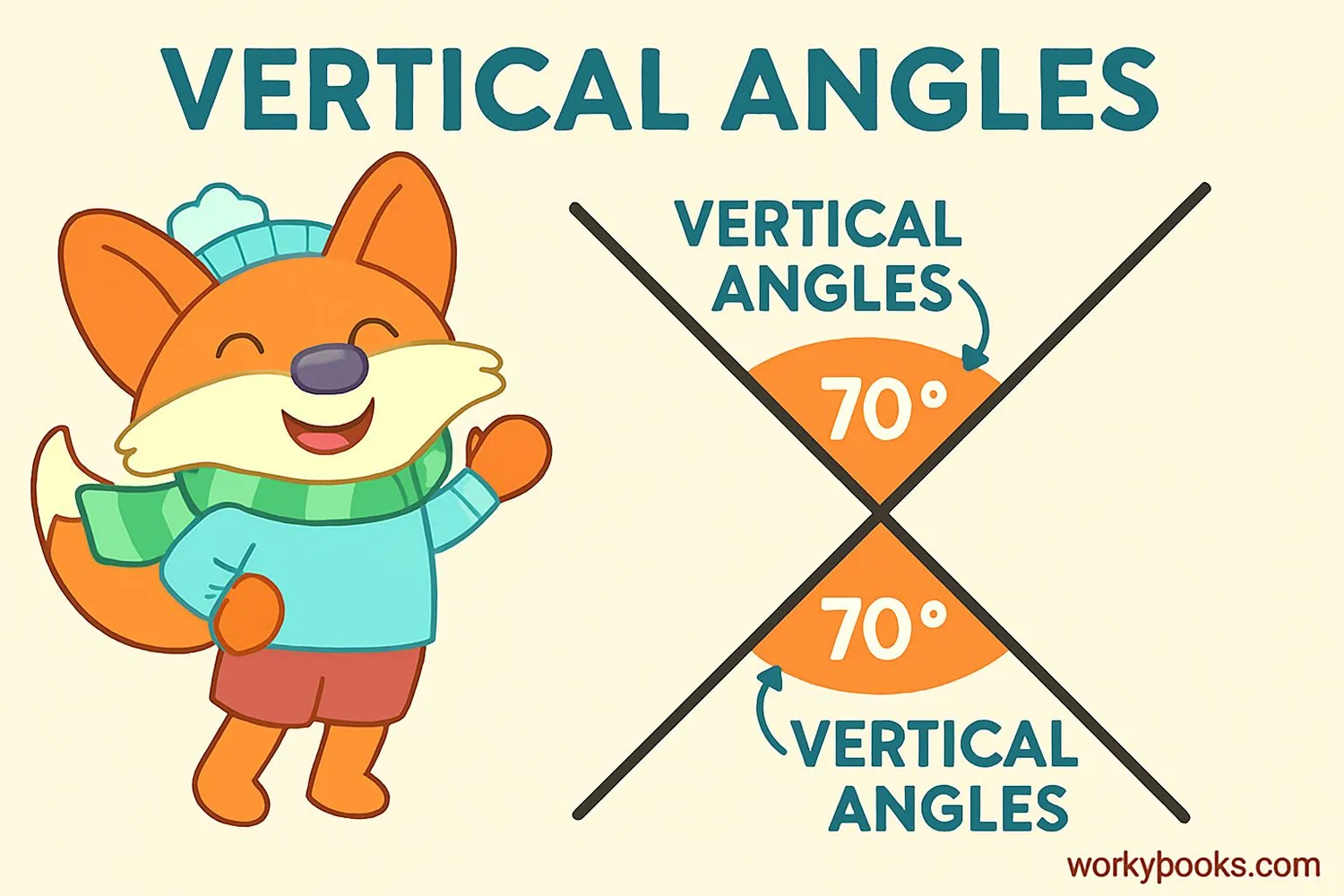
Vertical angles are a special pair of angles that form when two straight lines cross each other. They're also called opposite angles because they sit directly across from each other at the intersection point.
When two lines intersect, they create four angles. The angles that are opposite to each other are vertical angles. There are always two pairs of vertical angles when two lines cross.
What makes vertical angles special? They're always equal in measure! If one vertical angle is 60°, the angle opposite it will also be 60°. This is true no matter how the lines cross.
Key Concept
Vertical angles are formed by two intersecting lines and are always equal to each other.
Properties of Vertical Angles
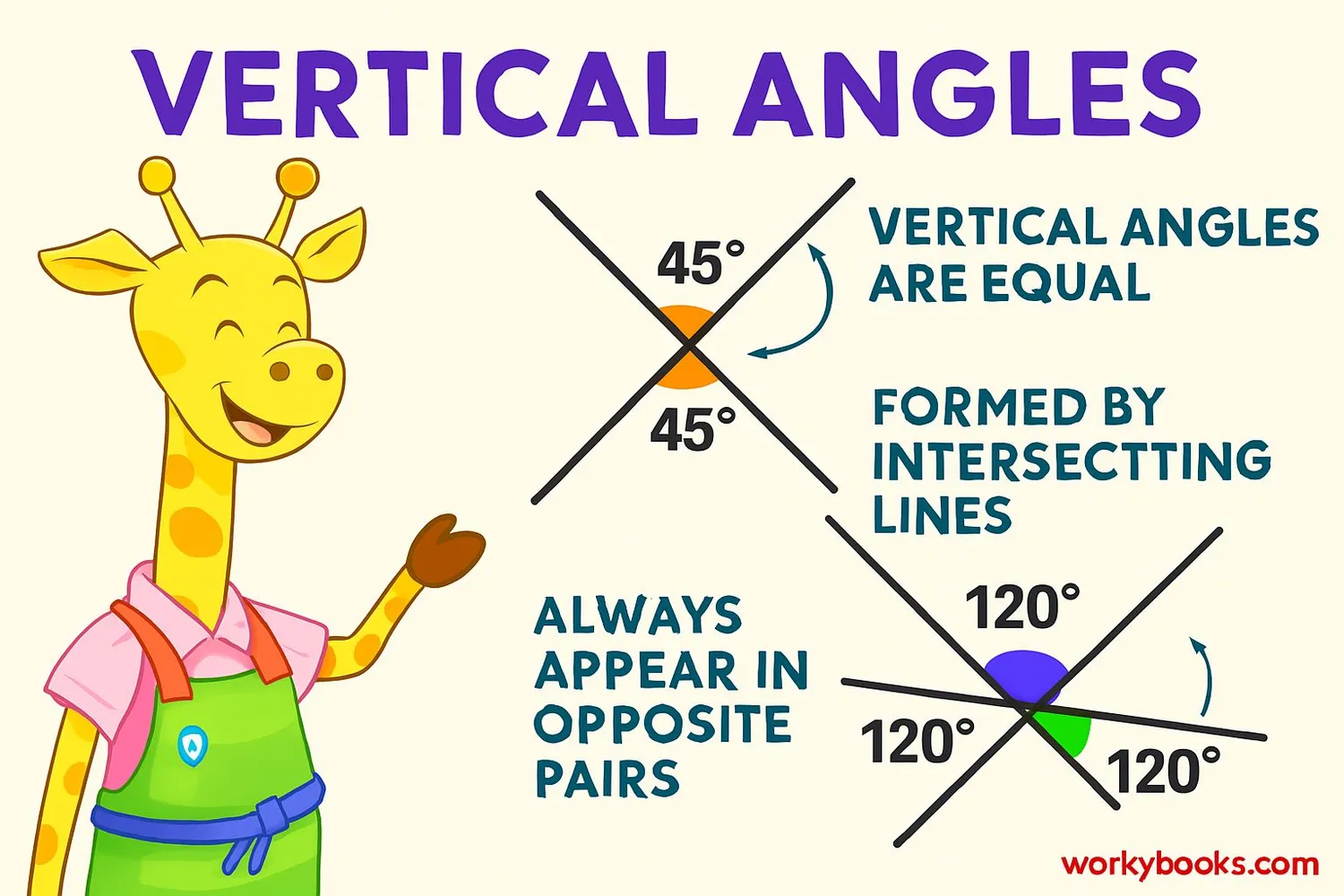
Vertical angles have some special properties that make them different from other types of angles:
Equal Measure
Vertical angles are always equal to each other. If one angle is 45°, the vertical angle opposite it will also be 45°.
Opposite Position
Vertical angles are always opposite each other when two lines cross. They never sit next to each other.
Non-Adjacent
Vertical angles are not next to each other. They are separated by the other angles formed at the intersection.
Supplementary to Adjacent Angles
Each vertical angle is supplementary to the angles next to it, meaning they add up to 180°.
Remember
Vertical angles are equal because they are formed by the same two lines and are opposite each other at the intersection point.
Examples of Vertical Angles

Vertical angles appear all around us in everyday objects and shapes:
Example 1: Scissors - When you open scissors, the blades form two intersecting lines, creating vertical angles at the pivot point.
Example 2: Railroad Tracks - When two railroad tracks cross, they form vertical angles at the intersection.
Example 3: Letter "X" - The letter X is made of two lines crossing, creating two pairs of vertical angles.
Let's look at a mathematical example:
If two lines intersect and one vertical angle is 70°, what are the other angles?
- The opposite vertical angle will also be 70°
- The adjacent angles will be 180° - 70° = 110° each
Practice Tip
When you see two crossing lines, look for the angles that are opposite each other. These are vertical angles and must be equal!
Vertical Angles vs. Adjacent Angles
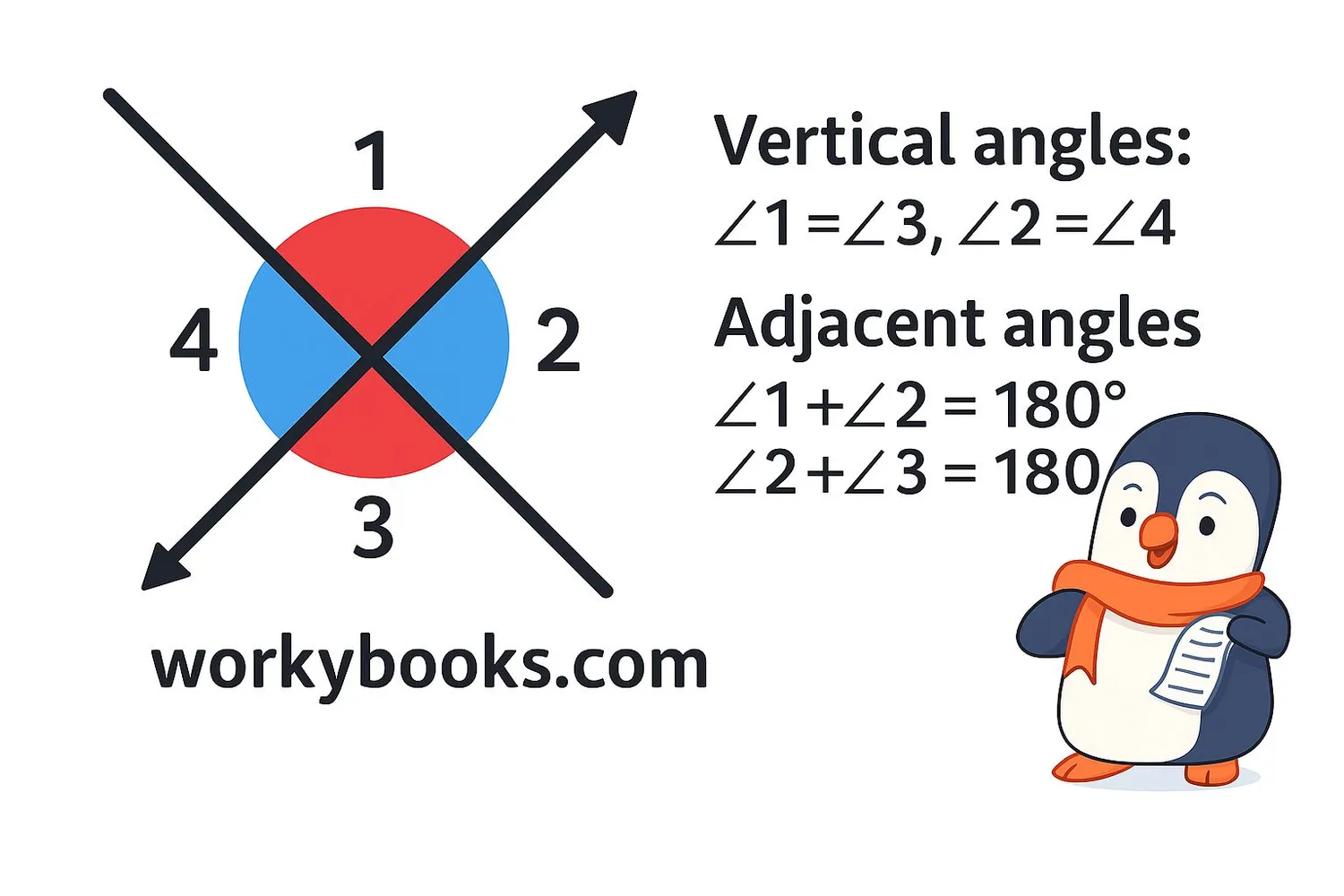
It's important to understand the difference between vertical angles and adjacent angles:
Vertical Angles:
- Opposite each other at the intersection
- Always equal in measure
- Not next to each other
Adjacent Angles:
- Next to each other, sharing a common side
- May or may not be equal
- Together form a straight line (180°)
When two lines intersect:
- Vertical angles are equal: ∠1 = ∠3 and ∠2 = ∠4
- Adjacent angles are supplementary: ∠1 + ∠2 = 180°, ∠2 + ∠3 = 180°, etc.
Vertical Angles
Opposite angles formed by intersecting lines. Always equal.
Adjacent Angles
Angles next to each other that share a common side. Supplementary (add to 180°).
Vertical Angles Practice Quiz
Test your knowledge of vertical angles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about vertical angles:
Angle Trivia
Discover interesting facts about angles and geometry:
Ancient Angle Masters
The ancient Egyptians were among the first to use angles extensively in architecture. They used right angles to build the pyramids with remarkable precision over 4,500 years ago.
Nature's Angles
Honeybees build honeycombs with perfect hexagonal cells that meet at 120-degree angles. This creates the strongest structure using the least amount of wax.
Angles in Space
Astronomers use angles to measure distances in space. The distance to stars is measured in parsecs, which comes from "parallax second" - a unit based on angles.
Most Vertical Angles
The most vertical angles you can create at a single point is theoretically unlimited! Each new line that passes through an existing intersection point creates more pairs of vertical angles.





