X Squared (x²) - Definition, Examples, Quiz, FAQ, Trivia
Learn the meaning of x squared with visual examples, practice problems, and interactive activities
What is X Squared?
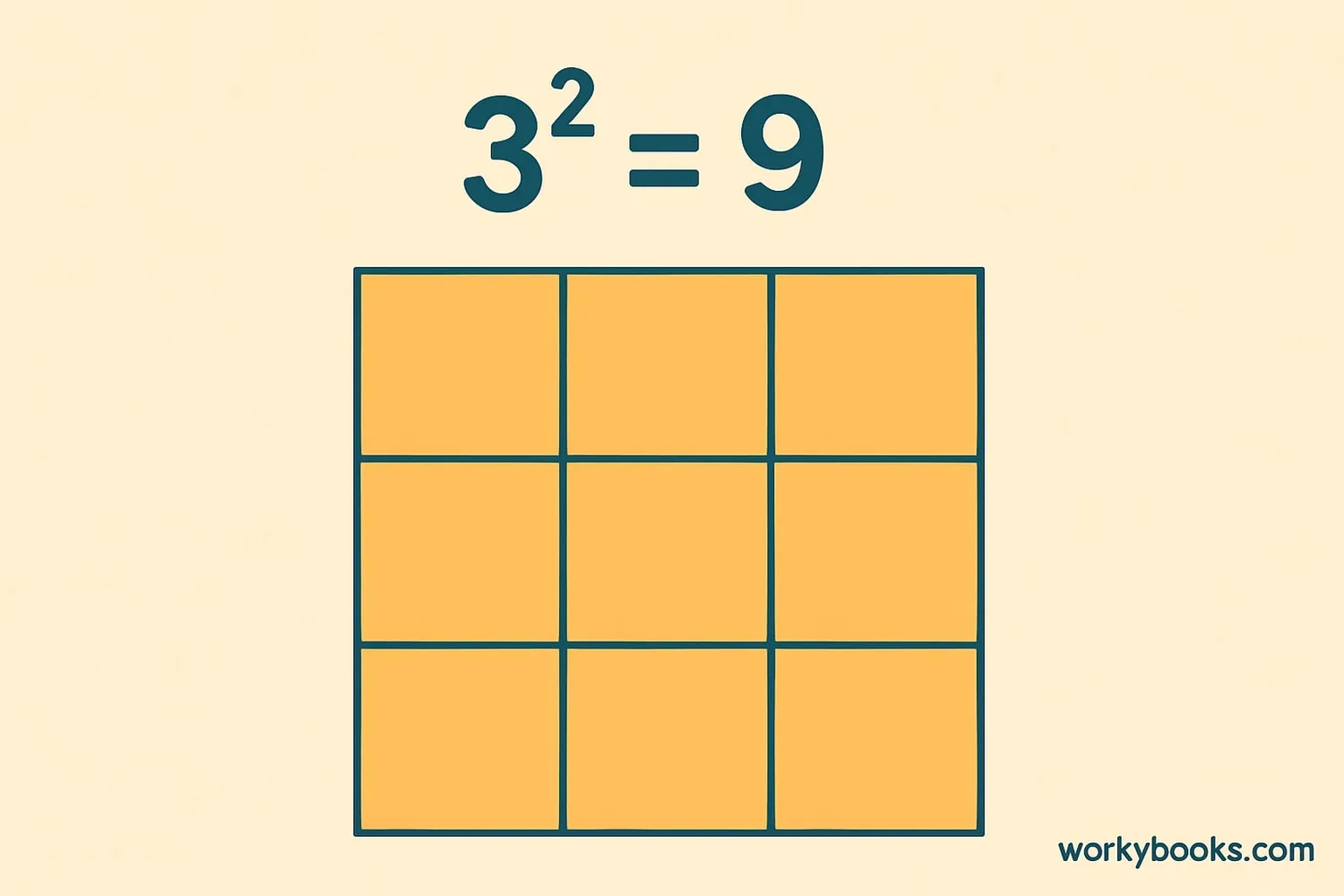
X squared (written as x²) means multiplying a number by itself. It's a special operation in math called "squaring" a number. When you see x², it tells you to take the number x and multiply it by itself.
Why is it important? Squaring numbers helps us solve many math problems, especially in algebra and geometry. It appears in formulas for area, equations, and patterns.
For example:
- If x = 4, then x² = 4 × 4 = 16
- If x = 5, then x² = 5 × 5 = 25
- If x = 10, then x² = 10 × 10 = 100
Key Concept
x² = x × x. This is the foundation for understanding squared numbers.
Perfect Squares
2² = 4
3² = 9
4² = 16
5² = 25
Numbers like 1, 4, 9, 16, 25 are perfect squares
Exponent Notation
The small 2 is called an exponent and means "squared"
Algebraic Meaning
x squared equals x multiplied by itself
Calculating x²
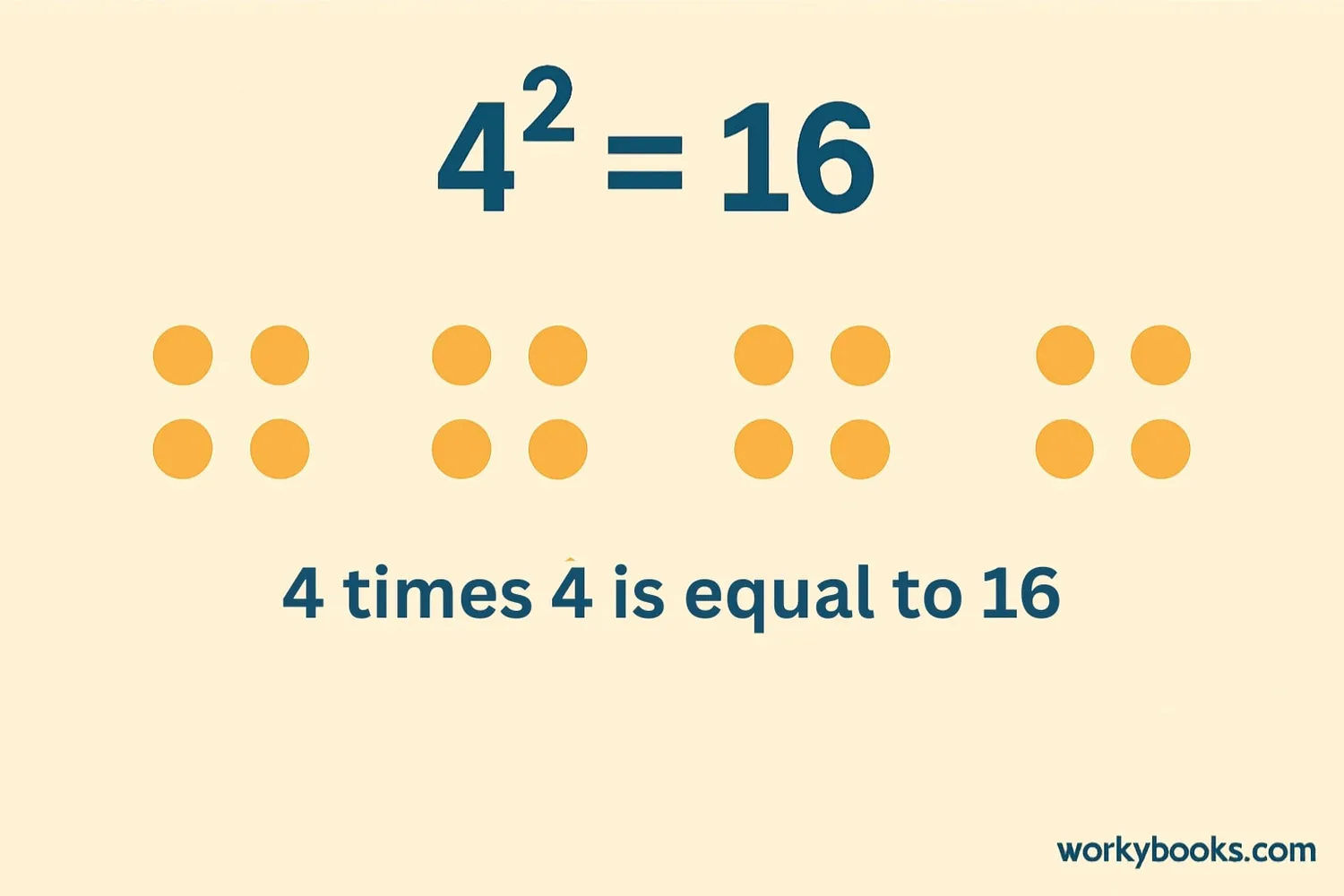
Calculating x squared is simple once you understand the concept. Here's how to do it:
Step 1: Identify the value of x
Step 2: Multiply that number by itself
Step 3: The result is x squared
Let's practice with examples:
Example 1: Calculate 6²
Solution: 6 × 6 = 36
Example 2: What is 9 squared?
Solution: 9 × 9 = 81
Example 3: Find the value of 12²
Solution: 12 × 12 = 144
Calculation Formula
To calculate any number squared, multiply it by itself
Remember
When you square a number, the result is always positive because multiplying two positive or two negative numbers gives a positive result.
The Graph of x²
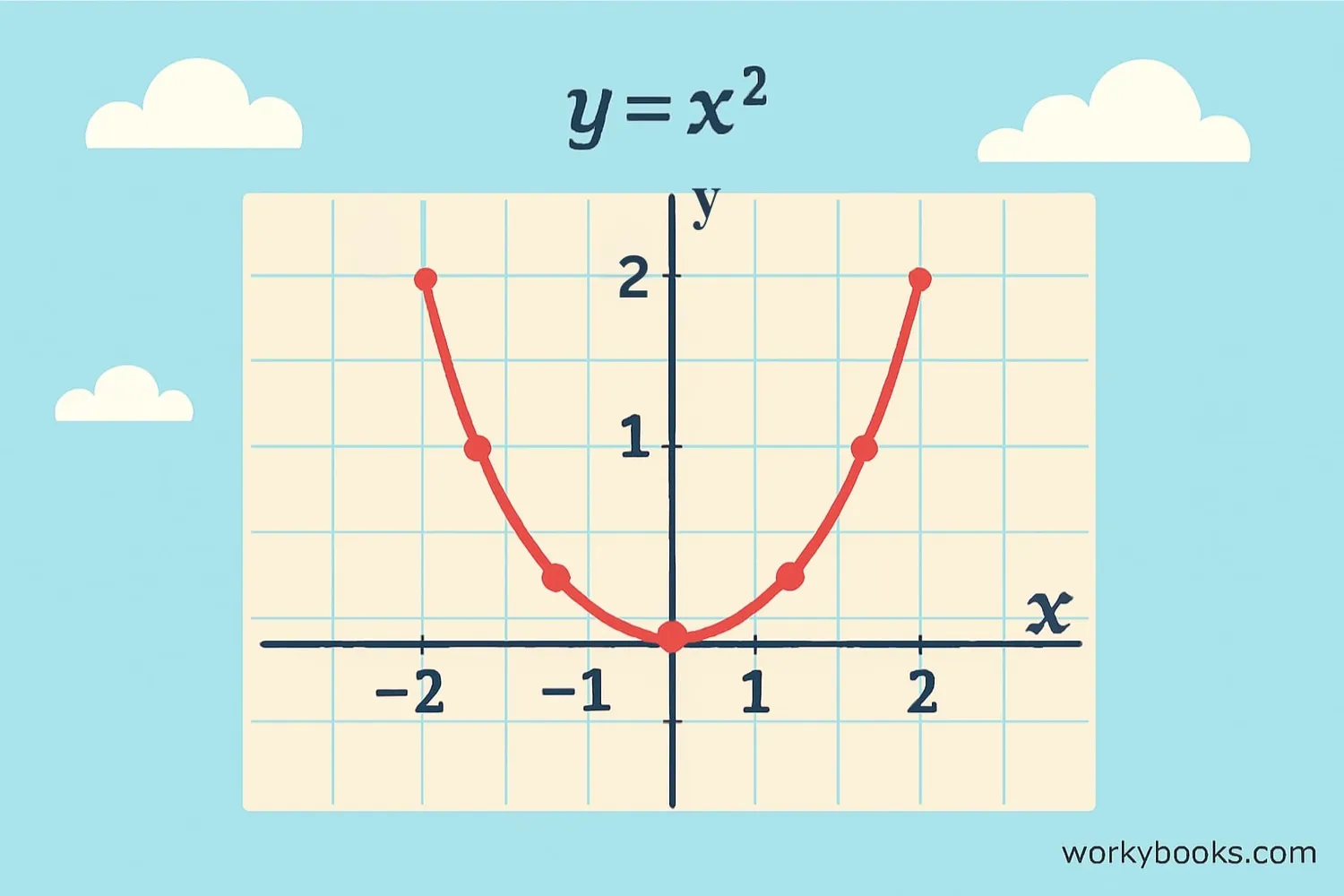
When we graph the equation y = x², we get a special U-shaped curve called a parabola. This graph has some interesting properties:
Shape: The graph is symmetric and looks like a U
Vertex: The lowest point is at (0,0)
Direction: It opens upward
Points:
- When x = 1, y = 1² = 1 → (1,1)
- When x = 2, y = 2² = 4 → (2,4)
- When x = -1, y = (-1)² = 1 → (-1,1)
- When x = -2, y = (-2)² = 4 → (-2,4)
Graph Tip
The parabola shape of y = x² appears in many real-world situations like the path of a thrown ball or the shape of satellite dishes.
| x-value | x² value | Point on graph |
|---|---|---|
| -3 | 9 | (-3,9) |
| -2 | 4 | (-2,4) |
| -1 | 1 | (-1,1) |
| 0 | 0 | (0,0) |
| 1 | 1 | (1,1) |
| 2 | 4 | (2,4) |
| 3 | 9 | (3,9) |
Square Root of x²
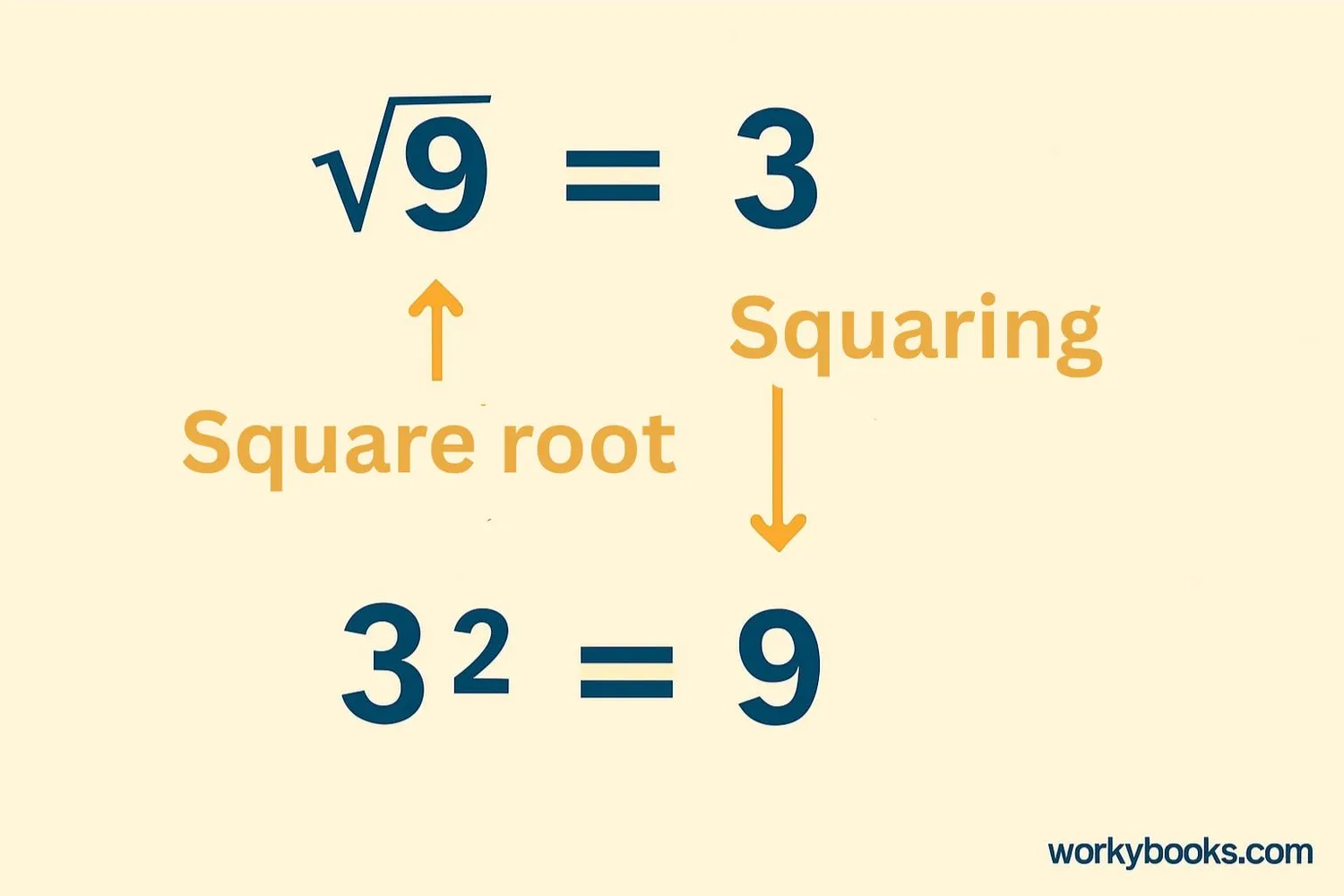
The square root of x² is a special relationship. The square root (√) is the opposite operation of squaring. When we take the square root of x², we get back to the original number, but with an important note:
Square Root Formula
The square root of x squared equals the absolute value of x
Examples:
Example 1: √(5²) = √25 = 5
Example 2: √((-3)²) = √9 = 3
Example 3: √(0²) = √0 = 0
This relationship helps us solve equations where we need to "undo" the squaring operation.
Remember
The square root of x² is always positive or zero, regardless of whether x was positive or negative.
Practice Quiz
Test your understanding of x squared with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about x squared:
Math Trivia
Discover interesting facts about squares and mathematics:
Ancient Mathematics
The concept of squaring numbers dates back to ancient Babylonian mathematics around 1800 BCE. They used clay tablets to solve quadratic equations.
Square Numbers Pattern
The difference between consecutive square numbers forms an arithmetic sequence: 1, 4, 9, 16, 25 → differences: 3, 5, 7, 9 (increasing by 2 each time).
Squared in Physics
Einstein's famous equation E=mc² includes a squared term. The c² means the speed of light multiplied by itself, which is a very large number!
Largest Square Number
The largest square number calculated is 2⁸²⁵⁸⁹⁹³³, which has over 24 million digits. It would take about 5,000 pages to write it out!





