45-45-90 Triangles - Definition, Examples, Quiz, FAQ, Trivia
Learn about special right triangles with easy explanations, formulas, examples, and practice activities
What is a 45-45-90 Triangle?
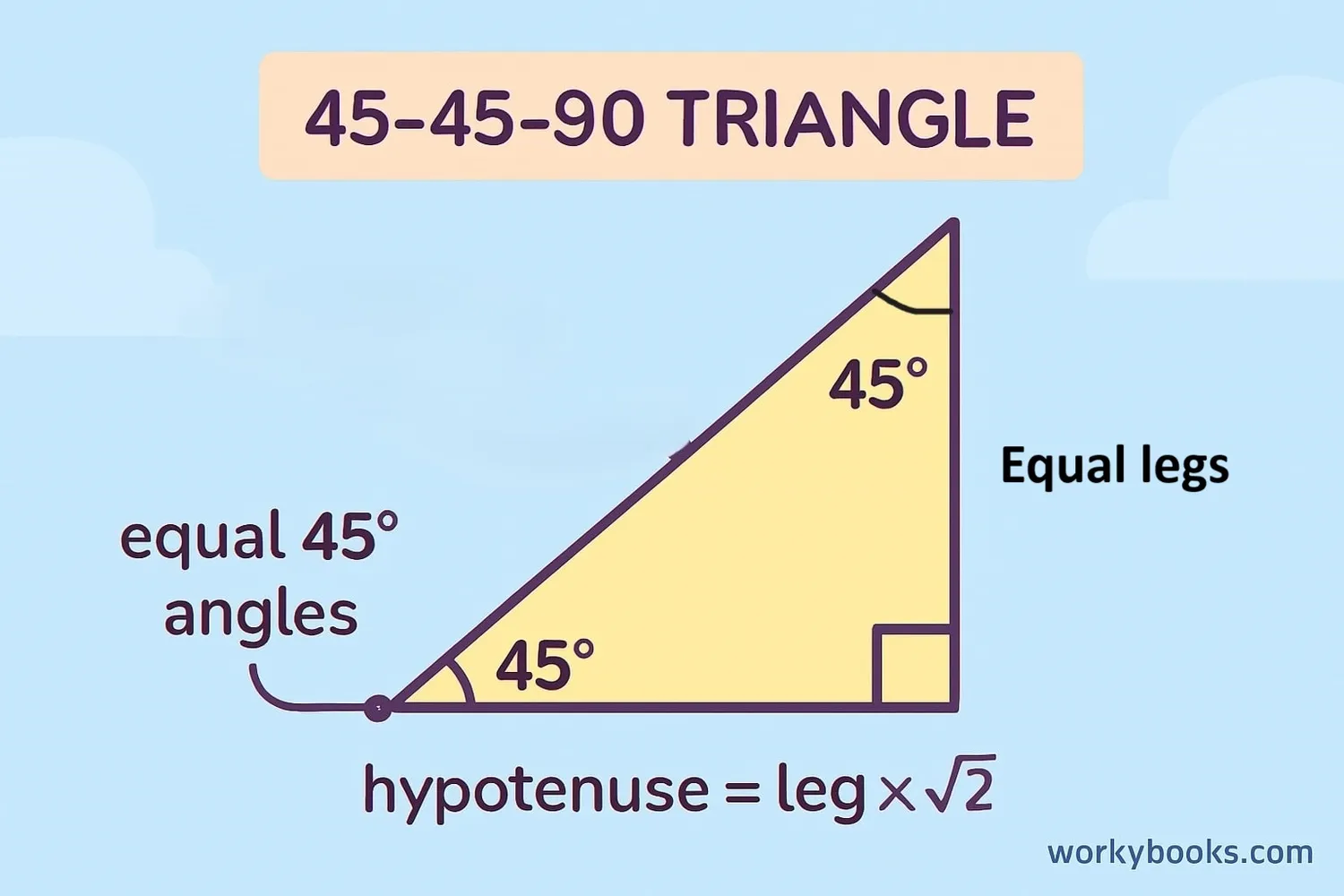
A 45-45-90 triangle is a special type of right triangle. It has two angles that measure 45 degrees each and one right angle that measures 90 degrees.
Because it has two equal angles, it also has two equal sides. This makes it an isosceles triangle as well as a right triangle. The two sides that form the right angle are called the legs, and they are always equal in length.
The side opposite the right angle is called the hypotenuse, and it's always longer than the legs. In a 45-45-90 triangle, the hypotenuse is always √2 times longer than each leg.
Key Concept
In a 45-45-90 triangle:
- Two angles are 45° each
- One angle is 90°
- Two sides (legs) are equal
- Hypotenuse = leg × √2
Properties of 45-45-90 Triangles
45-45-90 triangles have special properties that make them different from other triangles:
1. Angle Measures: Always has two 45° angles and one 90° angle. The sum of all angles is 180°, just like any other triangle.
2. Side Length Ratios: The ratio of the sides is always 1 : 1 : √2. This means that if one leg is length 'a', the other leg is also 'a', and the hypotenuse is 'a√2'.
3. Isosceles: Because it has two equal angles, it also has two equal sides (the legs). This makes it an isosceles right triangle.
4. Symmetry: It has one line of symmetry that bisects the 90° angle and the hypotenuse, creating two smaller 45-45-90 triangles.
5. Relationship to Squares: When you draw a diagonal in a square, it divides the square into two 45-45-90 triangles. This is why these triangles are so common in geometry!
Remember
In any 45-45-90 triangle, the legs are always equal, and the hypotenuse is always √2 times longer than each leg.
Formulas for 45-45-90 Triangles
Because of their special properties, we have simple formulas to work with 45-45-90 triangles:
Hypotenuse Formula
Where 'a' is the length of a leg and 'c' is the length of the hypotenuse.
Area Formula
Where 'a' is the length of a leg.
Perimeter Formula
Where 'a' is the length of a leg.
Real-World Examples
Let's practice with some examples of 45-45-90 triangles:
Example 1: The legs of a 45-45-90 triangle measure 5 cm each. What is the length of the hypotenuse?
Solution: Hypotenuse = leg × √2 = 5 × √2 ≈ 5 × 1.414 = 7.07 cm
Example 2: A square has sides measuring 10 cm. What is the length of its diagonal?
Solution: The diagonal divides the square into two 45-45-90 triangles. The legs are 10 cm, so hypotenuse = 10√2 ≈ 14.14 cm
Example 3: The hypotenuse of a 45-45-90 triangle is 12 cm. How long are the legs?
Solution: Since hypotenuse = leg × √2, we can rearrange: leg = hypotenuse ÷ √2 = 12 ÷ √2 ≈ 12 ÷ 1.414 = 8.49 cm
Example 4: Find the area of a 45-45-90 triangle with legs 6 cm.
Solution: Area = (leg²) ÷ 2 = (6 × 6) ÷ 2 = 36 ÷ 2 = 18 cm²
Example 5: Calculate the perimeter of a 45-45-90 triangle with legs 4 cm.
Solution: Perimeter = leg(2 + √2) = 4(2 + 1.414) = 4(3.414) = 13.656 cm
Triangle Practice Quiz
Test your knowledge of 45-45-90 triangles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about 45-45-90 triangles:
Math Trivia
Discover interesting facts about triangles and geometry:
Ancient Knowledge
The ancient Egyptians used the 3-4-5 right triangle to re-establish property boundaries after the Nile River flooded each year. This practical application of geometry dates back to 2000 BC!
Pythagorean Theorem
While Pythagoras is credited with the famous theorem about right triangles, evidence shows that Babylonian mathematicians understood the relationship between triangle sides 1000 years earlier!
Triangles in Space
NASA engineers use special right triangles to calculate spacecraft trajectories. The precise angles help them navigate through space with minimal fuel consumption.
Triangle Structures
The strongest geometric shape is the triangle. This is why you see triangular patterns in bridges, towers, and roof supports. Triangles distribute weight evenly and resist deformation.





