Additive Identity vs Multiplicative Identity - Definition, Examples, Quiz, FAQ, Trivia
Learn about special math properties that keep numbers the same
What is Identity in Math?
In mathematics, an identity is a special number that doesn't change other numbers when you use it in an operation. There are two main identity properties:
1. Additive Identity - The number that doesn't change other numbers when you add it.
2. Multiplicative Identity - The number that doesn't change other numbers when you multiply by it.
These properties work with whole numbers, integers, fractions, decimals, and even with variables! They're like magic numbers that keep everything the same.
Key Concept
Additive Identity is 0 (zero) and Multiplicative Identity is 1 (one). These numbers are special because they don't change the value of other numbers in their operations.
Additive Identity

The additive identity is the number 0 (zero). When you add zero to any number, the number stays the same. This is called the identity property of addition.
Additive Identity Formula
For any number 'a', adding zero gives you the same number 'a'.
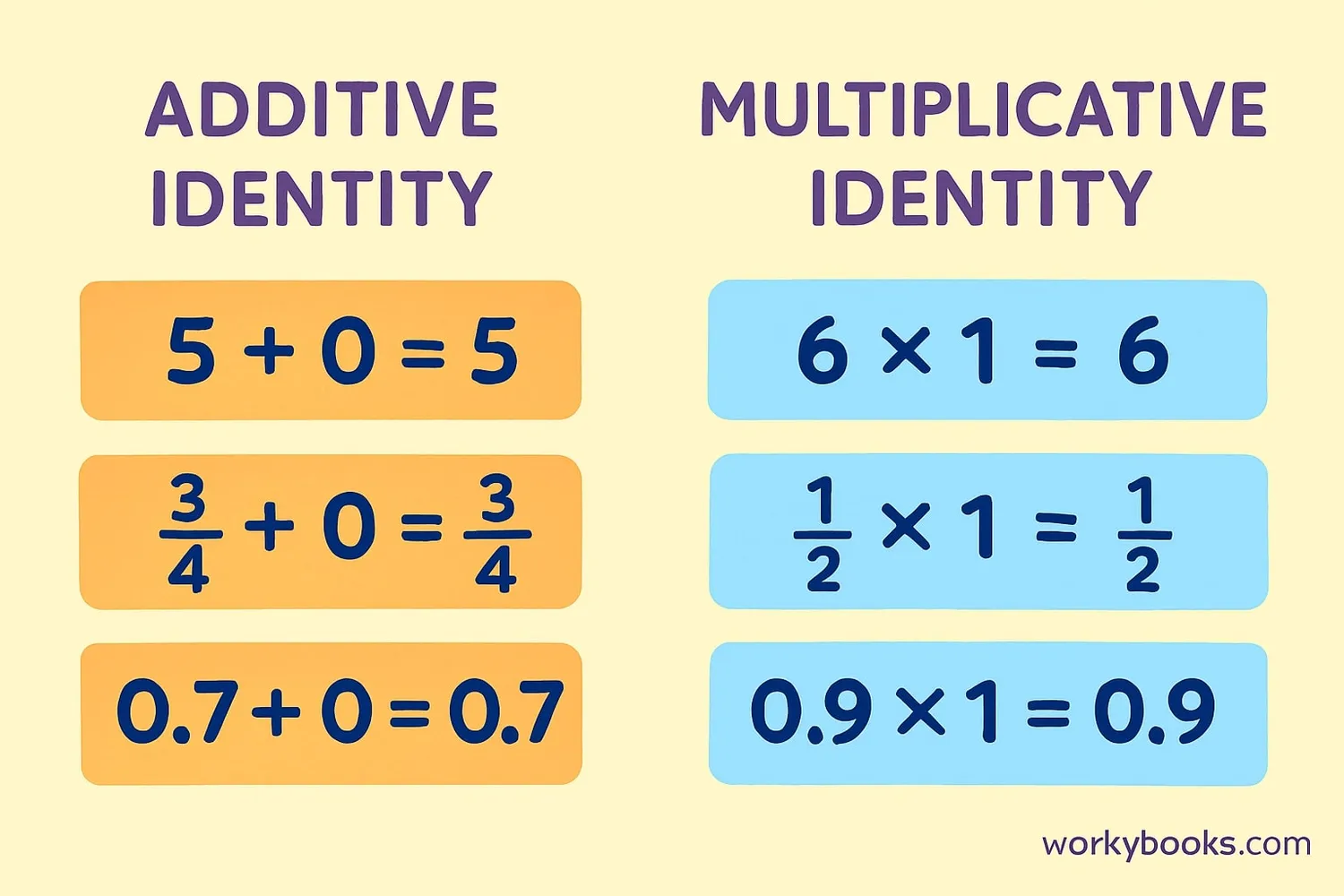
Example 1: 5 + 0 = 5
Example 2: 0 + 12 = 12
Example 3: 3.7 + 0 = 3.7
Example 4: 0 + (-8) = -8
This property works with all types of numbers: whole numbers, integers, fractions, decimals, and even with variables!
Remember
Zero is the only number that works as an additive identity. If you add any other number, the result will change.
Multiplicative Identity
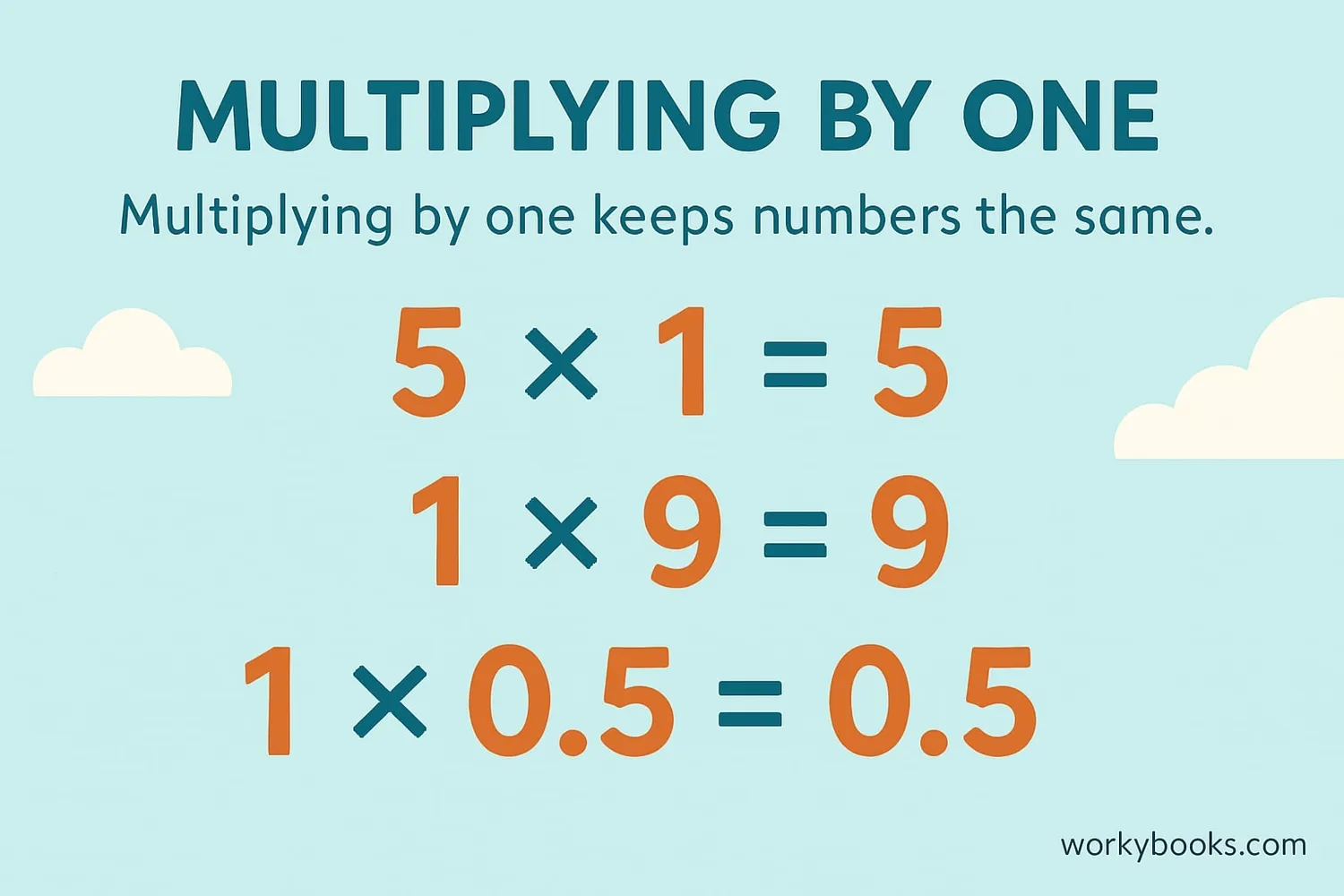
The multiplicative identity is the number 1 (one). When you multiply any number by one, the number stays the same. This is called the identity property of multiplication.
Multiplicative Identity Formula
For any number 'a', multiplying by one gives you the same number 'a'.
Example 1: 7 × 1 = 7
Example 2: 1 × 15 = 15
Example 3: 0.5 × 1 = 0.5
Example 4: 1 × (-4) = -4
Just like additive identity, this property works with all types of numbers. One is the only number that works as a multiplicative identity.
Remember
Multiplying by zero is different! When you multiply by zero, you get zero, not the original number.
Identity Properties Comparison
Let's compare the two identity properties side by side:
| Property | Additive Identity | Multiplicative Identity |
|---|---|---|
| Identity Number | 0 (Zero) | 1 (One) |
| Operation | Addition | Multiplication |
| Formula | a + 0 = a | a × 1 = a |
| Example with 5 | 5 + 0 = 5 | 5 × 1 = 5 |
| Example with 12 | 12 + 0 = 12 | 12 × 1 = 12 |
| Example with fraction (½) | ½ + 0 = ½ | ½ × 1 = ½ |
| Example with decimal (3.7) | 3.7 + 0 = 3.7 | 3.7 × 1 = 3.7 |
| Example with negative (-4) | -4 + 0 = -4 | -4 × 1 = -4 |
Important Note
These identity properties work with all numbers: whole numbers, natural numbers, integers, fractions, decimals, and even irrational numbers!
Solved Examples
Let's solve some problems using the identity properties:
Example 1: Using Additive Identity
What is 27 + 0?
Solution: Since adding zero doesn't change a number, 27 + 0 = 27
Example 2: Using Multiplicative Identity
What is 1 × 48?
Solution: Since multiplying by one doesn't change a number, 1 × 48 = 48
Example 3: With Fractions
What is ¾ × 1?
Solution: Multiplying by one keeps the fraction the same, so ¾ × 1 = ¾
Example 4: With Decimals
What is 0 + 6.25?
Solution: Adding zero doesn't change the decimal, so 0 + 6.25 = 6.25
Example 5: With Variables
Simplify: x + 0
Solution: Adding zero to any variable keeps it the same, so x + 0 = x
Practice Tip
When you see +0 or ×1 in a math problem, you can simply remove them because they don't change the value!
Identity Properties Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about identity properties:
Math Trivia
Discover interesting facts about numbers and identity properties:
Zero's Journey
The concept of zero as a number developed in India around the 5th century. It took several more centuries for the idea to spread to Europe, where it revolutionized mathematics.
Identity in Algebra
Identity properties are essential in algebra. When solving equations, we often use these properties to simplify expressions without changing their values.
Computer Math
In computer programming, identity properties are used to optimize calculations. Adding zero or multiplying by one are efficient operations that computers can process quickly.
Beyond Numbers
Identity properties extend beyond numbers. In matrix algebra, there are identity matrices that serve similar purposes for matrix operations.





