Arcs in Geometry - Definition, Examples, Quiz, FAQ, Trivia

What is an Arc?

An arc is part of the circumference of a circle. Think of it as a curved piece of the circle's edge between two points.

Just like a slice of pizza is part of the whole pizza, an arc is a "slice" of the circle's boundary. The two points where the arc begins and ends are called its endpoints.

The length of an arc is a portion of the circle's circumference. To understand arcs, it helps to know these important circle parts:

• Circumference - The distance around the entire circle
• Radius - The distance from the center to any point on the circle
• Diameter - The distance across the circle through the center

Types of Arcs

There are two main types of arcs:

Minor Arc: The shorter arc between two points on a circle. It measures less than 180 degrees. We usually name minor arcs with just two letters, like arc AB.

Major Arc: The longer arc between two points on a circle. It measures more than 180 degrees. We name major arcs with three letters to show the direction, like arc ACB.

There's also a special type called a Semicircle, which is exactly half of a circle (180 degrees). It's the longest minor arc possible.

Angles in Arcs

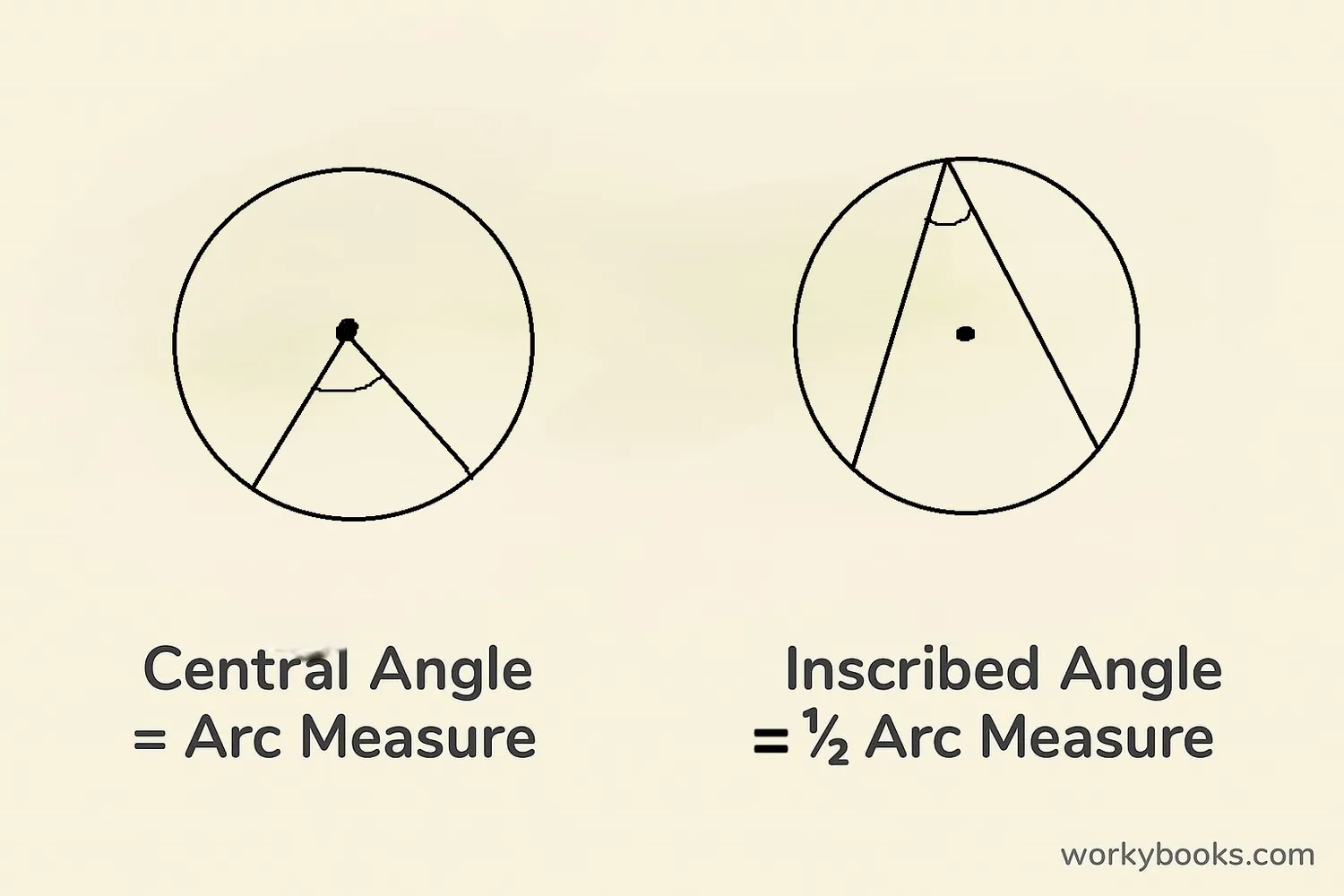
Angles help us measure arcs. There are two important angles related to arcs:

Central Angle: An angle formed by two radii (lines from center to circumference) at the center of the circle. The measure of a central angle equals the measure of its intercepted arc.

Inscribed Angle: An angle formed by two chords (lines connecting two points on the circle) that meet at a point on the circle. The measure of an inscribed angle is half the measure of its intercepted arc.

Here's how they work:

• If a central angle is 60°, its arc is also 60°
• If an inscribed angle is 30°, its arc is 60°
• The arc "intercepted" by an angle is the arc between the angle's two sides

Measuring Arcs

We can measure arcs in two ways:

Arc Measure: This is the angle at the center of the circle, measured in degrees. A full circle is 360°, so a semicircle is 180°.

Arc Length: This is the actual distance along the curved part of the arc. We calculate it using this formula:

Example: Calculate the length of a 90° arc in a circle with radius 10 cm.
Step 1: θ = 90°, r = 10 cm
Step 2: L = (90 ÷ 360) × 2 × π × 10
Step 3: L = (0.25) × 2 × 3.14159 × 10 ≈ 15.708 cm

The circumference of the full circle would be about 62.8 cm, so this 90° arc is one-fourth of that.

Real-World Examples

Arcs are all around us! Here are some common examples:

Rainbows: Natural arcs formed by sunlight and water droplets

Pizza Slices: The curved edge of a pizza slice is an arc

Bridges: Many bridges have arched designs that follow circular arcs

Clocks: The path the tip of a clock's hand follows is an arc

Basketball Hoops: The rim of a basketball hoop is a circular arc

Playground Slides: Many slides have curved sections that form arcs

Arc Knowledge Quiz

Test what you've learned with this 5-question quiz. Choose the best answer for each question.

Frequently Asked Questions

Here are answers to common questions about arcs:

Arc Trivia

Discover interesting facts about arcs: