Area and Perimeter of Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate the area and perimeter of different types of triangles with easy explanations and practice activities
What is a Triangle?
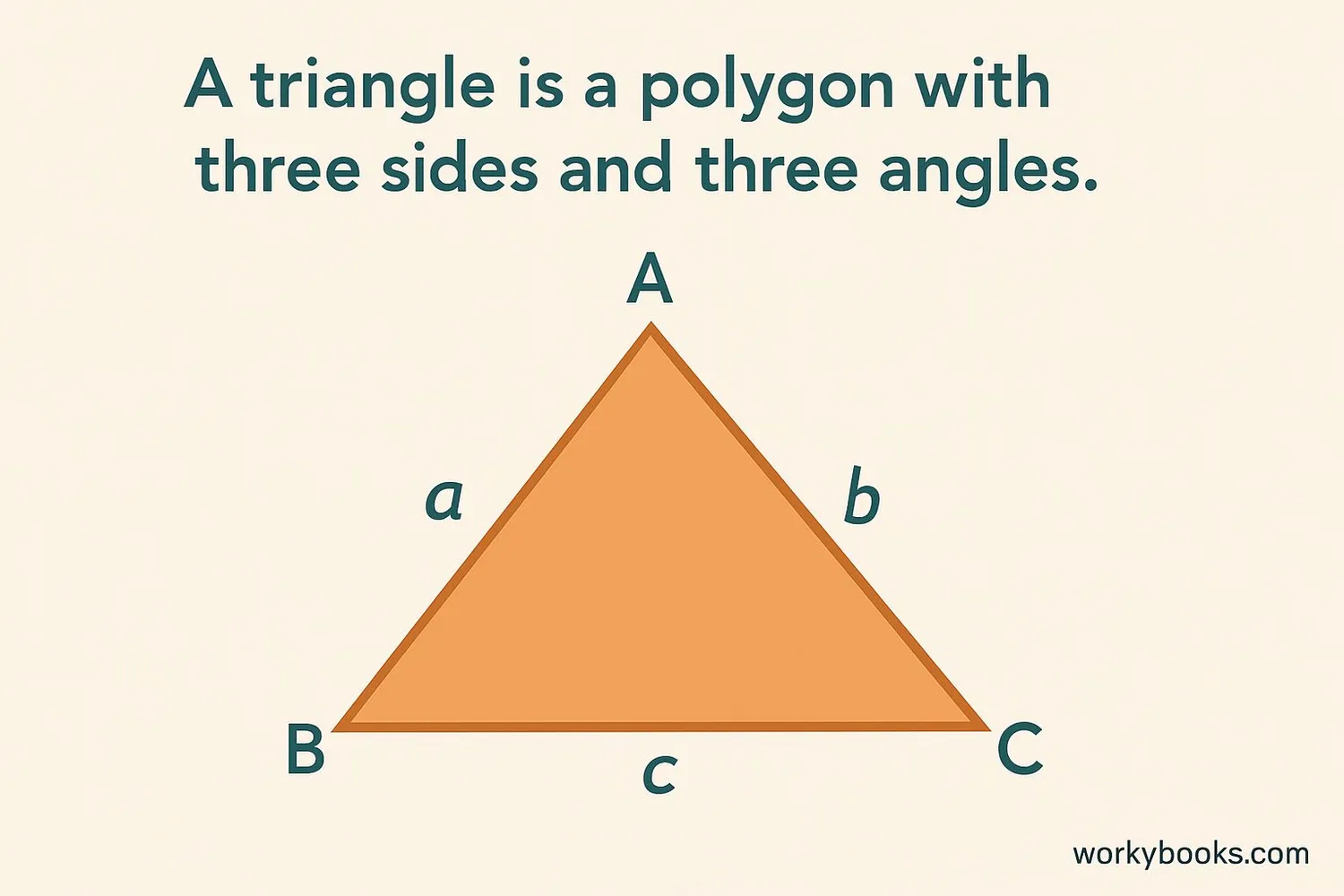
A triangle is a two-dimensional shape with three straight sides and three angles. It's one of the most basic shapes in geometry and has some special properties:
- All triangles have three sides and three angles
- The sum of all angles in a triangle always equals 180 degrees
- Triangles are classified by their side lengths and angle measurements
Triangles are everywhere in our world! You can find them in bridges, roofs, and even in the slices of pizza. Understanding triangles helps us build strong structures and solve many real-world problems.
Key Concept
A triangle is a closed shape with three straight sides and three angles that always add up to 180 degrees.
Perimeter of a Triangle
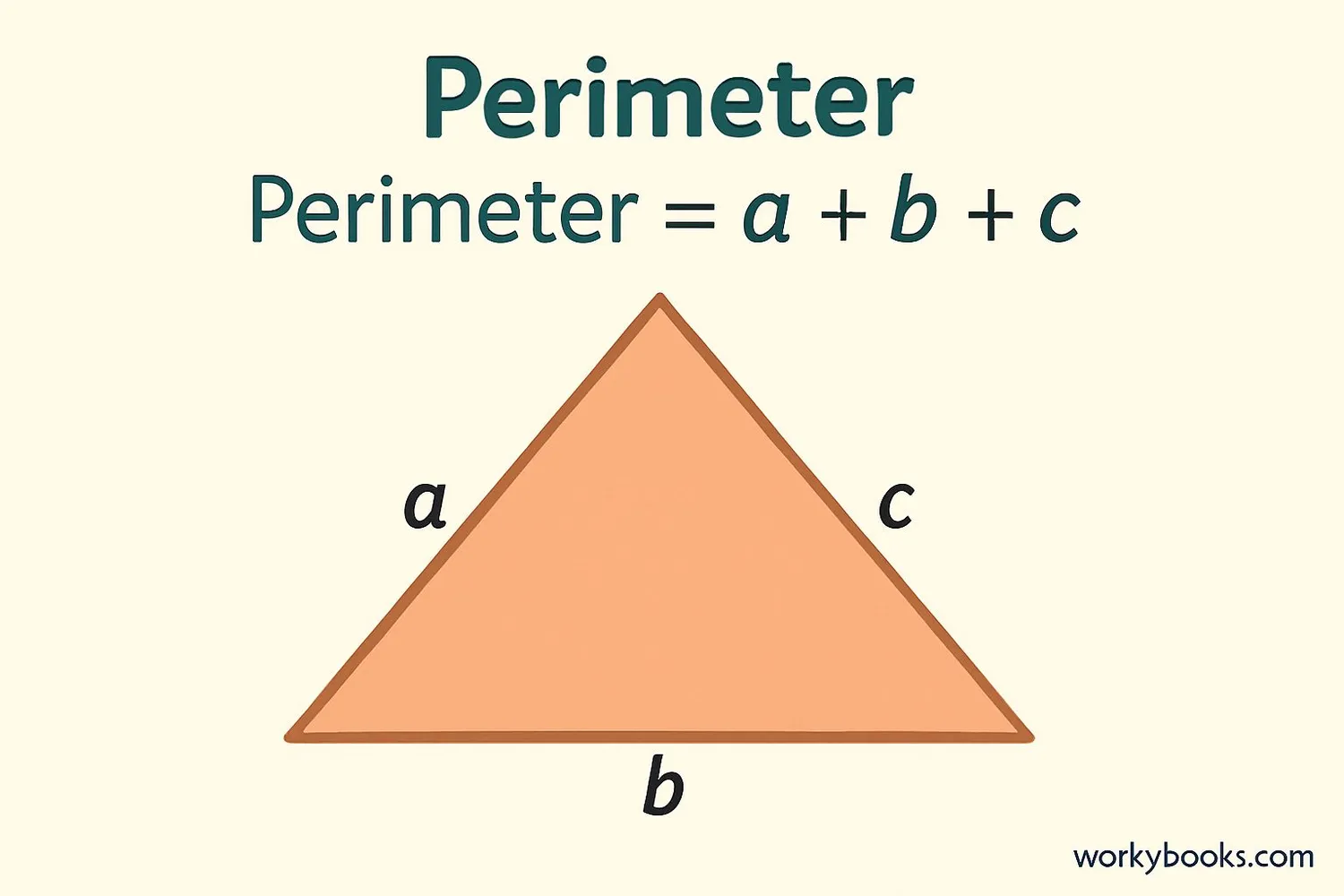
The perimeter of a triangle is the total distance around the outside of the shape. To find the perimeter, simply add the lengths of all three sides together.
Perimeter Formula
Where a, b, and c are the lengths of the three sides of the triangle.
Example: A triangle has sides measuring 5 cm, 7 cm, and 9 cm. What is its perimeter?
Step 1: Identify the side lengths → a=5cm, b=7cm, c=9cm
Step 2: Add them together → 5 + 7 + 9
Step 3: Calculate the result → 21 cm
So the perimeter of this triangle is 21 centimeters.
Remember
Perimeter is always measured in linear units (like cm, m, in). It's the total length of the boundary around the shape.
Area of a Triangle
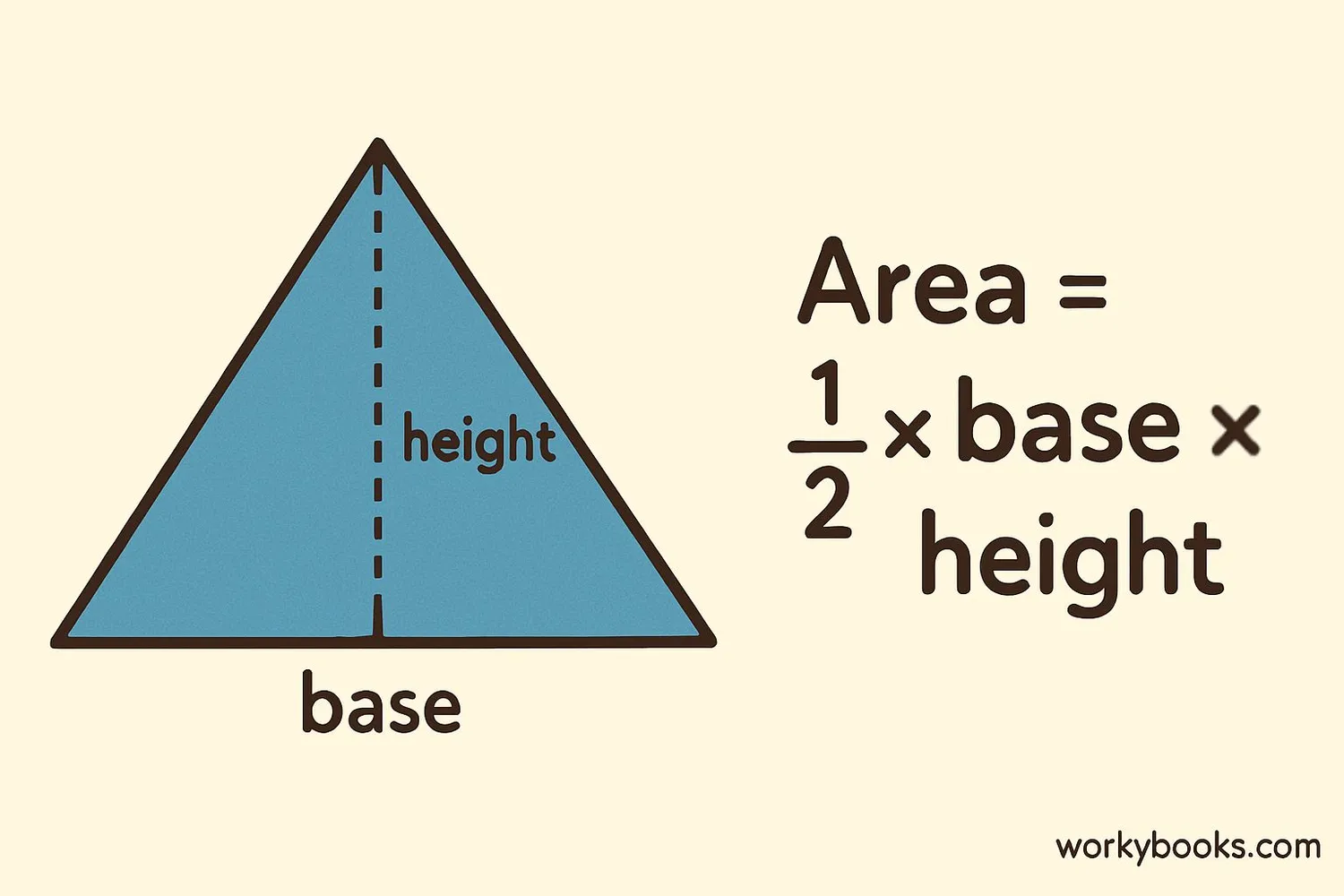
The area of a triangle is the amount of space inside the shape. To calculate the area, you need to know the base and the height of the triangle.
Area Formula
Where b is the base and h is the height of the triangle.
Example: A triangle has a base of 10 cm and a height of 6 cm. What is its area?
Step 1: Identify base and height → b=10cm, h=6cm
Step 2: Multiply base by height → 10 × 6 = 60
Step 3: Multiply by ½ → 60 × 0.5 = 30
Step 4: Add units → 30 cm²
So the area of this triangle is 30 square centimeters.
Important Note
The height must always be perpendicular (at a right angle) to the base. Area is always measured in square units (like cm², m², in²).
Types of Triangles
Triangles can be classified in different ways based on their sides and angles. Here are the main types:
Equilateral Triangle
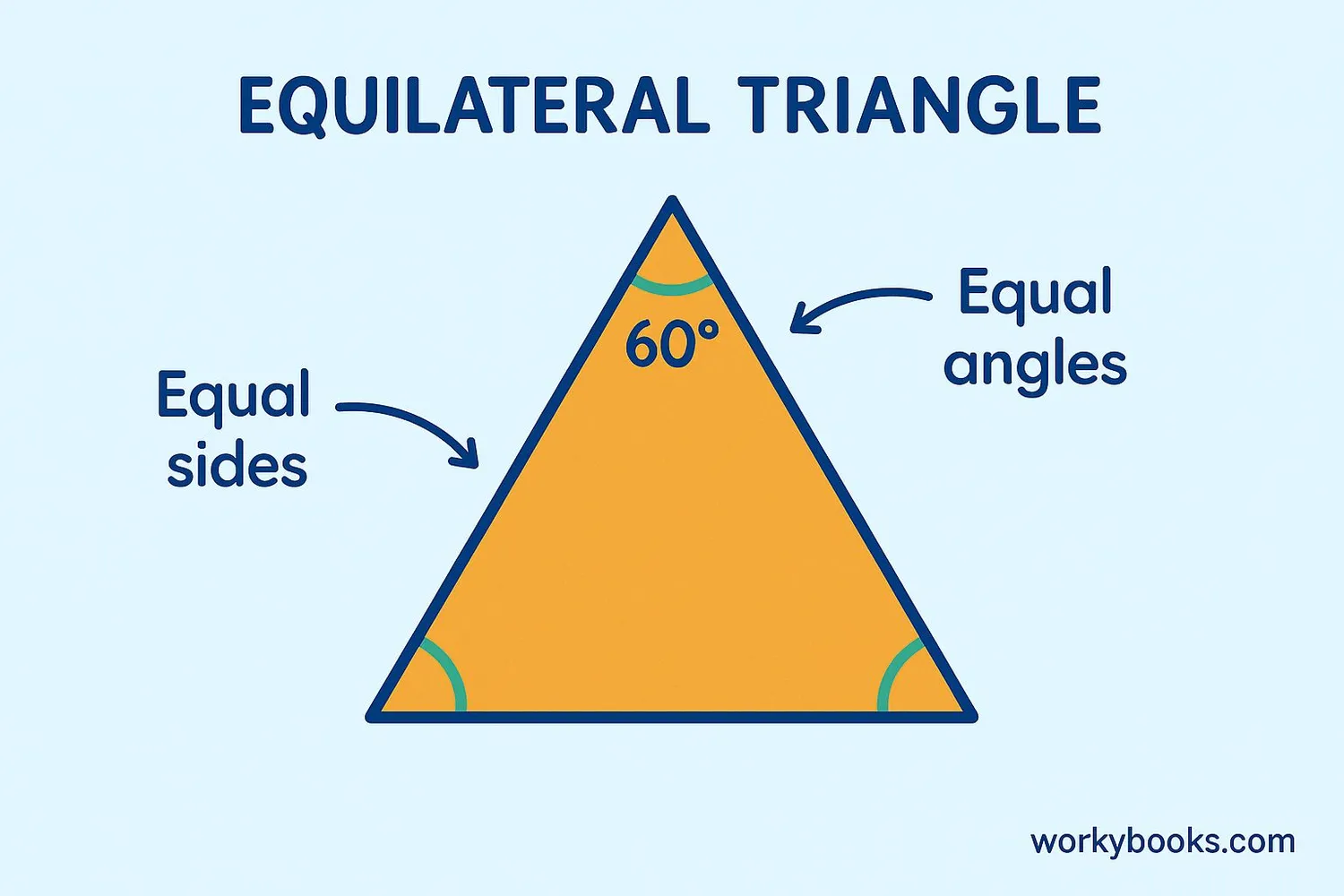
All three sides equal length
All three angles equal 60°
Isosceles Triangle
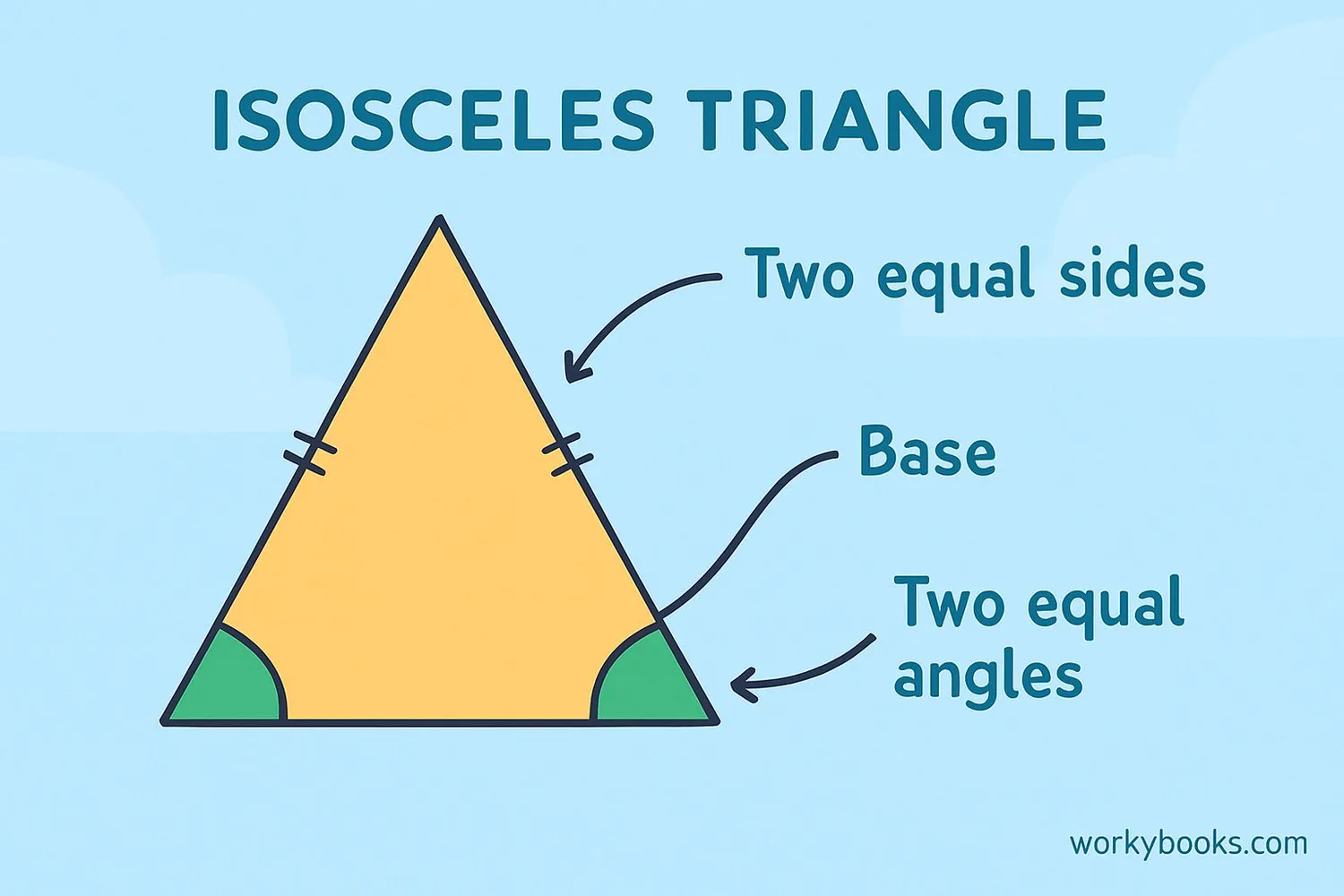
Two sides equal length
Two angles equal measure
Scalene Triangle
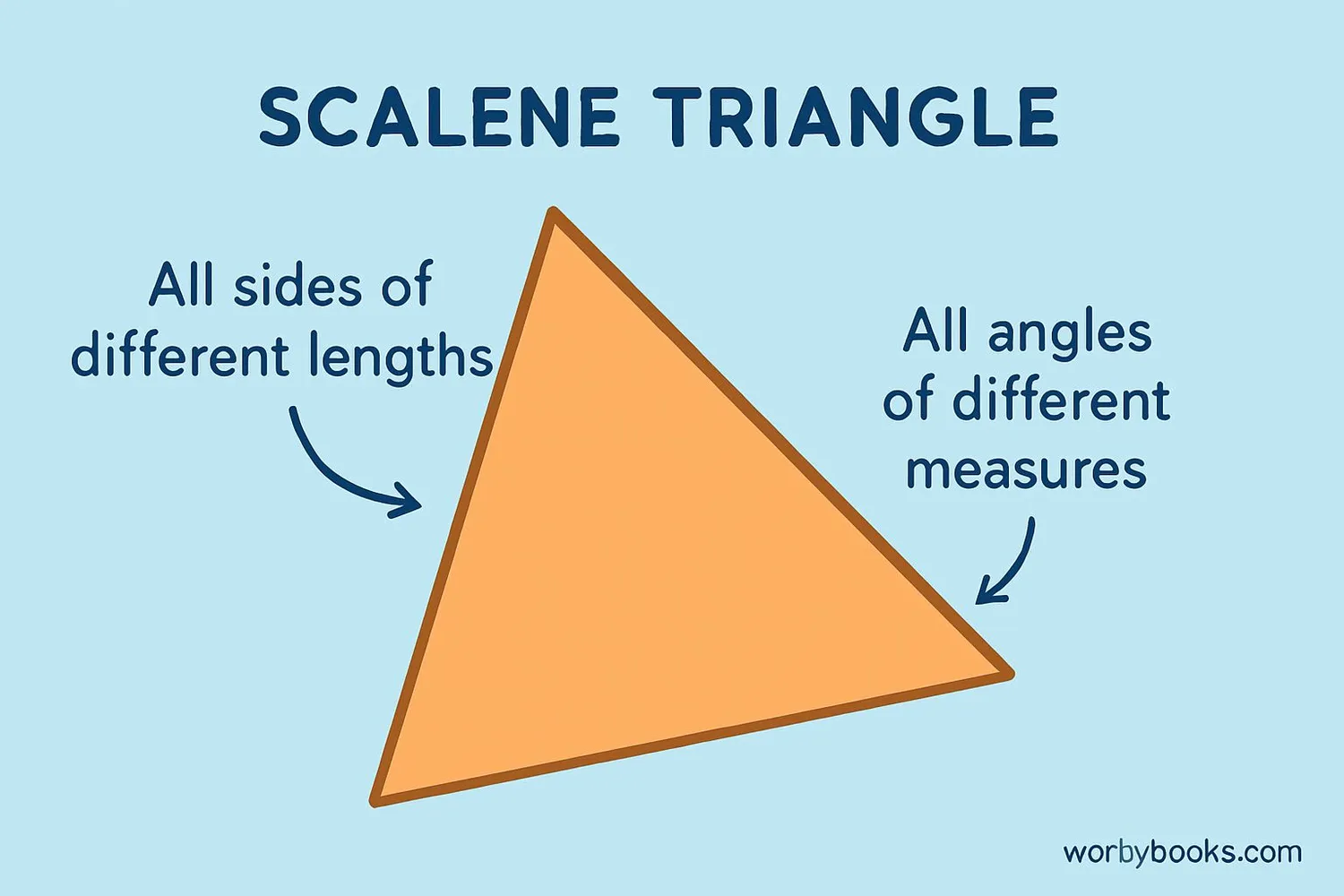
All sides different lengths
All angles different measures
Perimeter and Area for Different Triangle Types
| Triangle Type | Perimeter Formula | Area Formula |
|---|---|---|
| Equilateral | P = 3 × side | A = (√3/4) × side² |
| Isosceles | P = 2 × equal side + base | A = ½ × base × height |
| Scalene | P = a + b + c | A = ½ × base × height |
Remember
No matter what type of triangle it is, the area is always calculated using base and height: A = ½ × b × h
Solved Examples
Let's solve some real-world problems using what we've learned about area and perimeter of triangles:
Example 1: Perimeter Calculation
A triangular garden has sides measuring 8m, 10m, and 12m. What length of fencing is needed to enclose it?
Solution:
Perimeter = Sum of all sides
P = 8m + 10m + 12m = 30m
Answer: 30 meters of fencing is needed.
Example 2: Area Calculation
A triangular flag has a base of 40cm and height of 25cm. What is its area?
Solution:
Area = ½ × base × height
A = ½ × 40cm × 25cm = ½ × 1000 = 500 cm²
Answer: The flag has an area of 500 square centimeters.
Example 3: Equilateral Triangle
An equilateral triangle has sides of 6cm each. Find its perimeter and area.
Solution:
Perimeter = 3 × side = 3 × 6cm = 18cm
Area = (√3/4) × side² = (1.732/4) × 36 ≈ (0.433) × 36 ≈ 15.588 cm²
Answer: Perimeter = 18cm, Area ≈ 15.6 cm²
Practice Tip
Always write down the formula first, then substitute the values you know. This helps avoid mistakes!
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about triangles:
Triangle Trivia
Discover interesting facts about triangles:
Ancient Triangles
The ancient Egyptians used triangles in building the pyramids around 2500 BC. They understood the properties of right triangles to create precise 90-degree angles.
Strongest Shape
Triangles are the strongest geometric shape. That's why you see them in bridges, cranes, and roofs. The triangular shape distributes weight evenly and resists deformation.
Space Triangles
NASA uses triangular shapes in spacecraft design because they are lightweight and strong. The Apollo lunar module had triangular windows to withstand pressure differences.
Largest Triangle
The largest triangle ever created was formed by three cities: London, Chicago, and Sydney. The distances between these cities form a giant triangle spanning the globe.


