Area Model Division - Definition, Examples, Quiz, FAQ, Trivia
Learn to divide multi-digit numbers using visual models and step-by-step methods
What is Area Model Division?
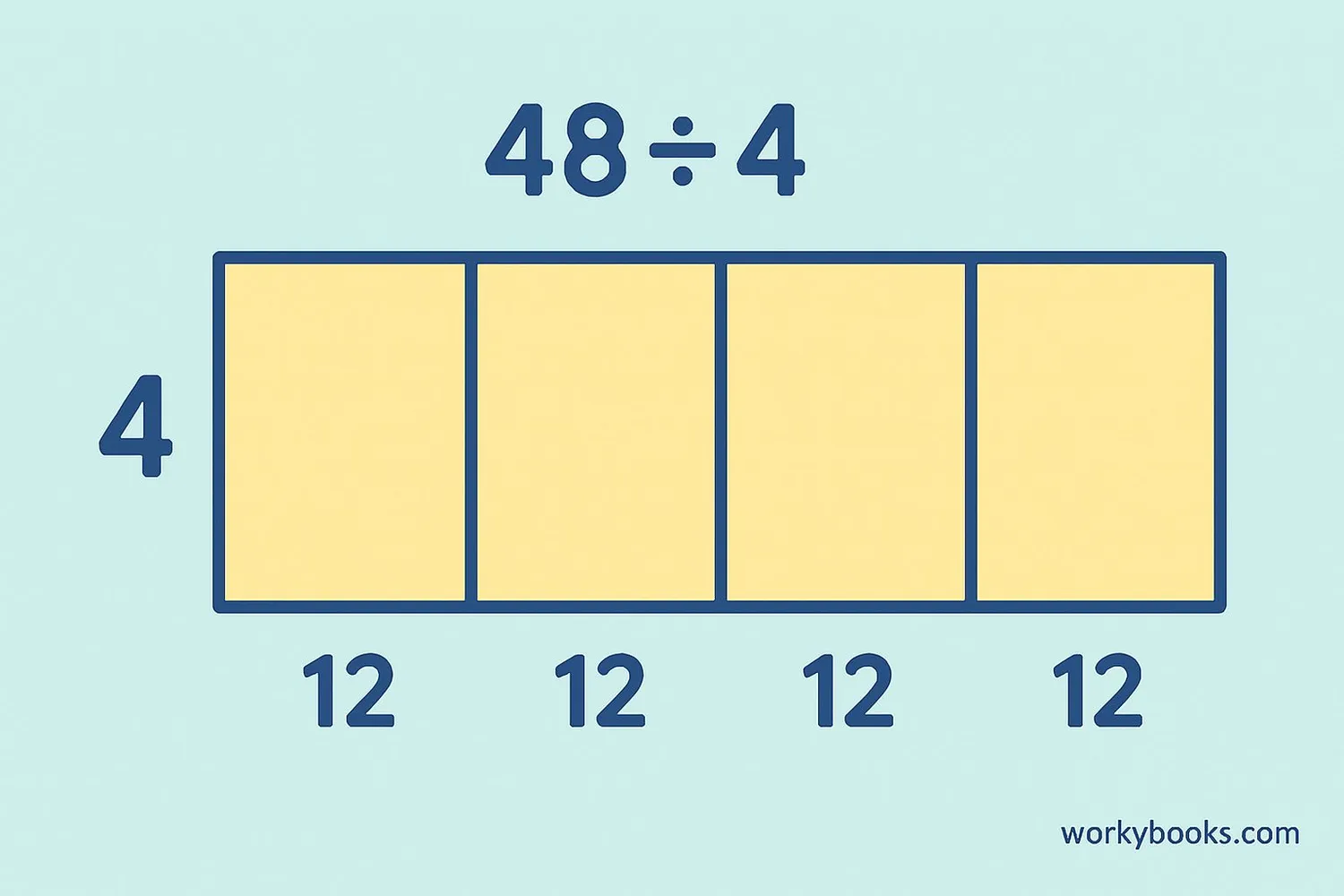
Area model division is a visual way to divide multi-digit numbers. It uses rectangles to represent division problems. The rectangle's area represents the dividend (the number being divided), and the rectangle's width represents the divisor (the number doing the dividing).
Why use area models? They help us:
- Understand division as splitting into equal parts
- Break large division problems into smaller, easier steps
- Visualize how partial quotients work
- See the relationship between division and multiplication
Key Concept
The area model connects division to multiplication: Dividend = Divisor × Quotient
How to Do Area Model Division
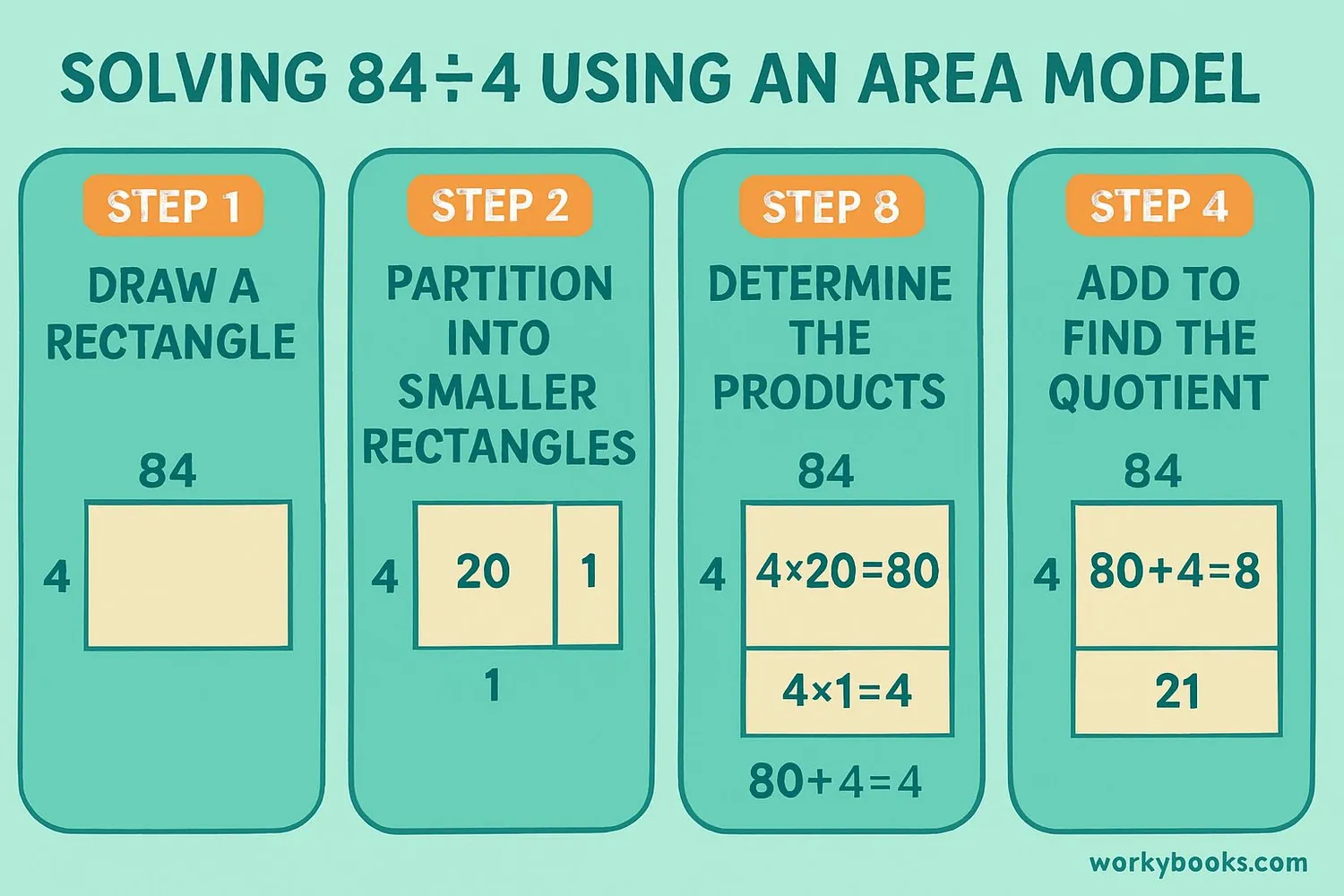
Follow these steps to solve division problems using the area model:
Draw a Rectangle
Draw a rectangle that will represent your division problem.
Label the Area
Write the dividend (the number being divided) inside the rectangle.
Divide the Rectangle
Split the rectangle into sections based on the divisor and place value.
Find Partial Quotients
Divide each section and write the partial quotients above each part.
Add the Quotients
Add all partial quotients to get the final answer.
Remember
The area model uses place value to break large numbers into smaller, easier-to-divide parts.
Area Model Division Examples
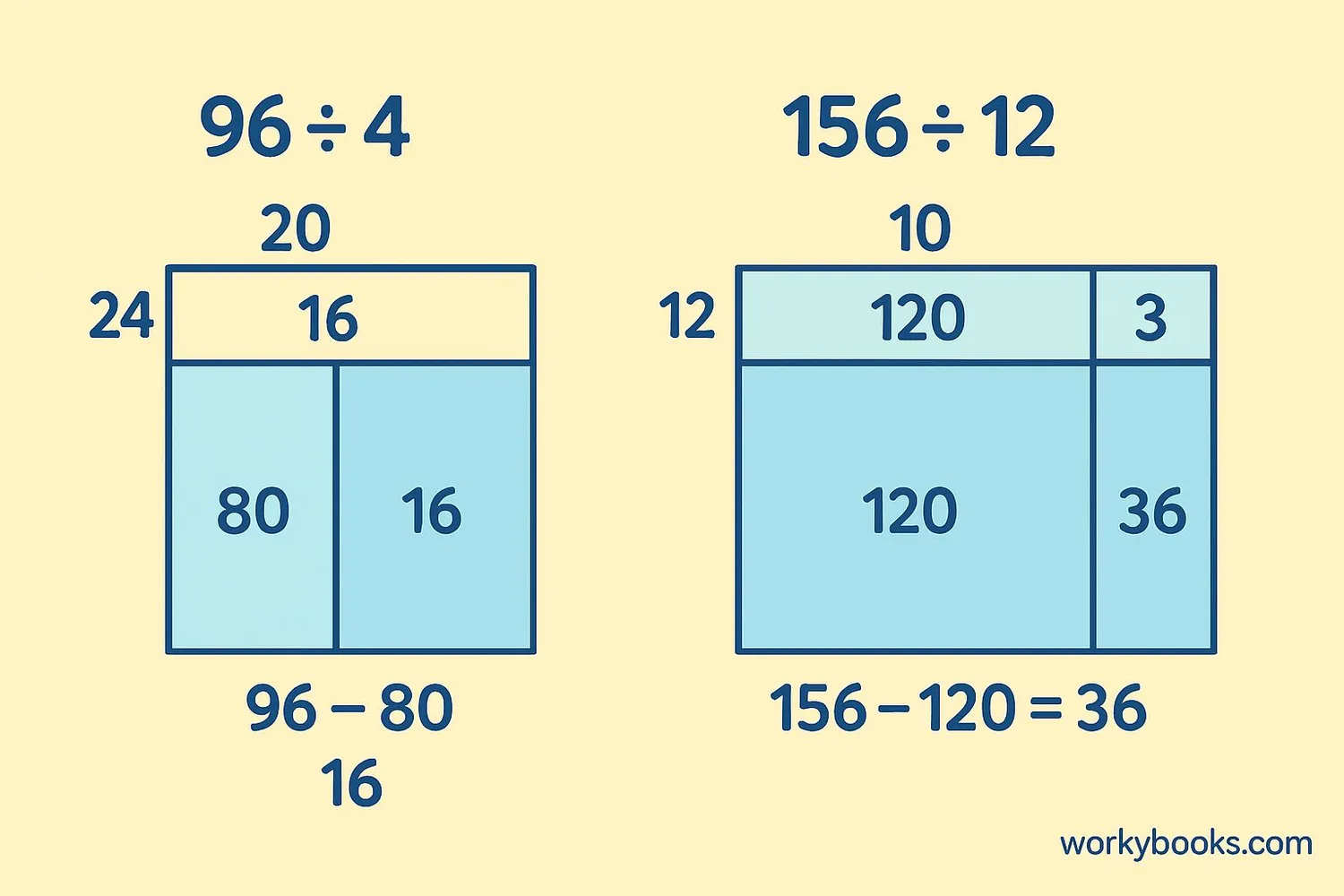
Example 1: 96 ÷ 4
1. Draw a rectangle and write 96 inside it.
2. Divide the rectangle into two parts: 80 and 16 (using place value).
3. Divide each part by 4: 80 ÷ 4 = 20, 16 ÷ 4 = 4
4. Add the partial quotients: 20 + 4 = 24
5. Answer: 96 ÷ 4 = 24
Example 2: 156 ÷ 12
1. Draw a rectangle and write 156 inside it.
2. Divide into parts: 120 and 36 (12 × 10 = 120, 12 × 3 = 36)
3. Divide each part by 12: 120 ÷ 12 = 10, 36 ÷ 12 = 3
4. Add partial quotients: 10 + 3 = 13
5. Answer: 156 ÷ 12 = 13
Example 3: Division with Remainder (75 ÷ 6)
1. Draw rectangle with 75 inside.
2. Divide into parts: 60 and 15 (6 × 10 = 60, 6 × 2 = 12)
3. Divide: 60 ÷ 6 = 10, 15 ÷ 6 = 2 with remainder 3
4. Add partial quotients: 10 + 2 = 12 with remainder 3
5. Answer: 75 ÷ 6 = 12 R3
Practice Tip
Start with smaller numbers and work your way up to larger division problems.
Area Model Division Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about area model division:
Math Trivia
Discover interesting facts about division and mathematics:
Ancient Division
The earliest known division algorithms date back to 2000 BCE in ancient Egypt. Egyptians used a method of doubling and halving to solve division problems.
Division in Nature
Division patterns appear throughout nature. Many plants grow in Fibonacci sequences (1, 1, 2, 3, 5, 8...), which involve division relationships between consecutive numbers.
Computer Division
Computers perform division using algorithms similar to area models. Modern processors use methods like Newton-Raphson iteration for fast division calculations.
Division Record
The largest division problem ever solved was 1 divided by 13, calculated to 10 trillion decimal places. It took 208 days of computer processing time!





