Area of a Sector of a Circle - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate portions of circles with easy explanations, visual examples, and practice activities
What is a Sector of a Circle?
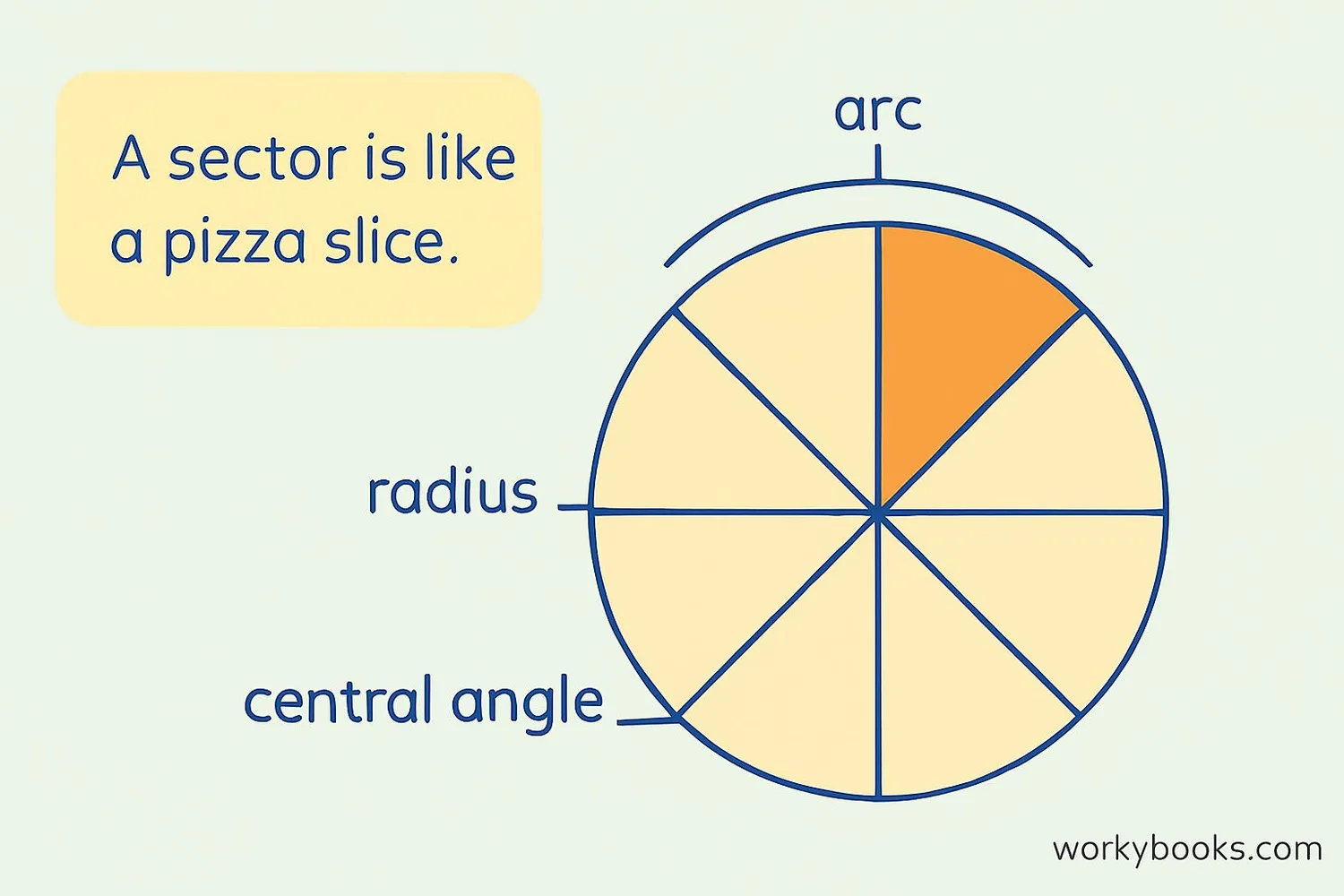
A sector of a circle is like a slice of pizza or a piece of pie. It's a portion of the circle that is enclosed by two radii (the plural of radius) and an arc.
Think of a circle as a whole pizza. When you cut it into slices, each slice is a sector! The crust part of the slice is the arc, and the straight edges from the center to the crust are the radii.
The size of the sector depends on the angle at the center. A small angle makes a small sector, while a large angle makes a big sector. The biggest sector would be the whole circle itself!
Key Concept
A sector is defined by two elements: the central angle (θ) and the radius (r) of the circle.
How to Find the Area of a Sector
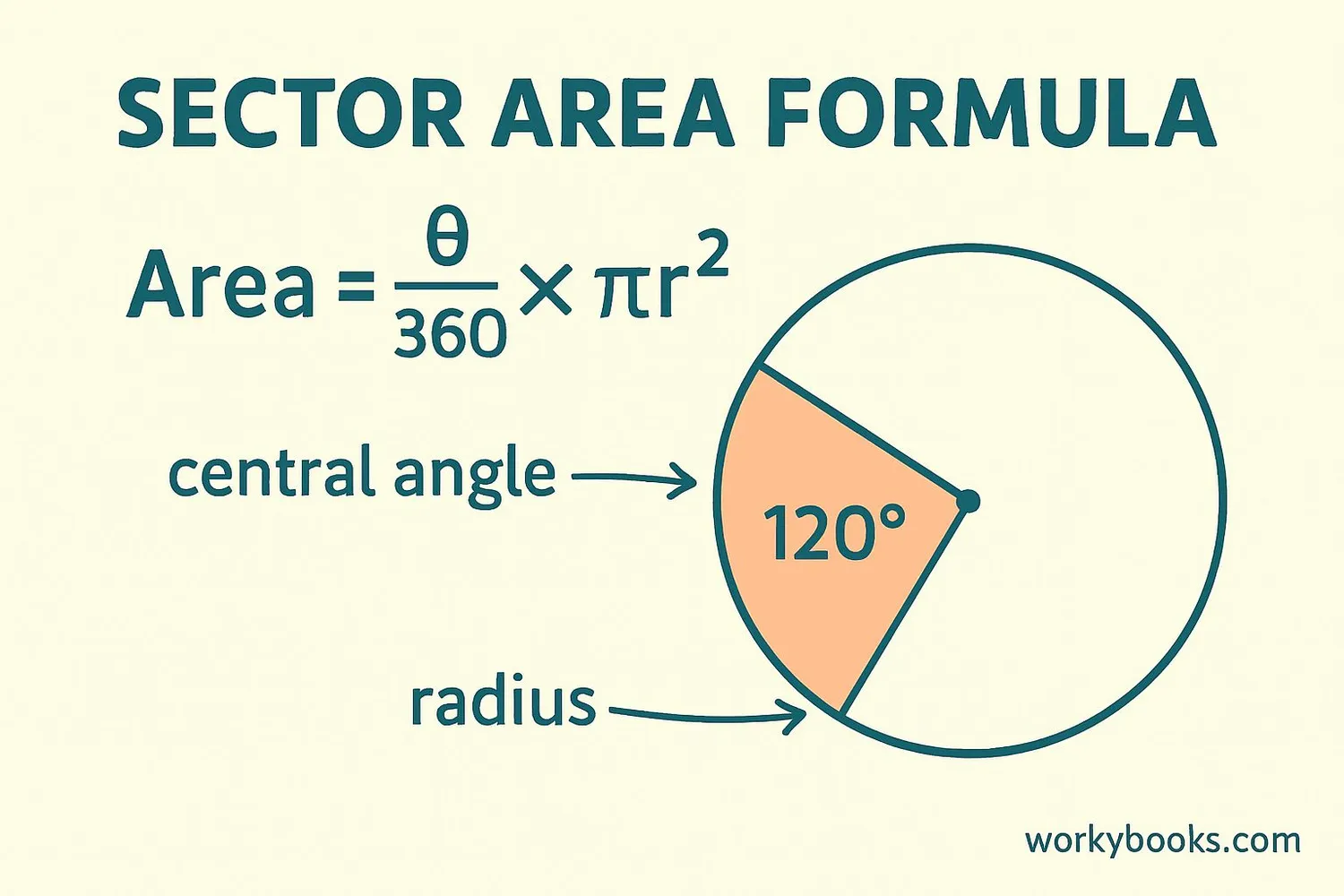
To find the area of a sector, we use a special formula that connects the sector to the whole circle:
Sector Area Formula
Where:
θ = central angle in degrees
r = radius of the circle
π ≈ 3.14159
The fraction (θ ÷ 360) tells us what portion of the whole circle our sector is. For example, a 90° sector is 90/360 = 1/4 of the circle.
Then we multiply this fraction by the area of the whole circle (πr²) to get just the area of our sector.
Example: Find the area of a sector with a 60° central angle in a circle with radius 6 cm.
Step 1: Calculate the fraction: 60 ÷ 360 = 1/6
Step 2: Calculate the circle area: π × 6² = 3.14 × 36 ≈ 113.04 cm²
Step 3: Multiply: (1/6) × 113.04 ≈ 18.84 cm²
Remember
The area of a sector is always a portion of the circle's total area. The bigger the central angle, the larger the sector area.
Real-World Examples
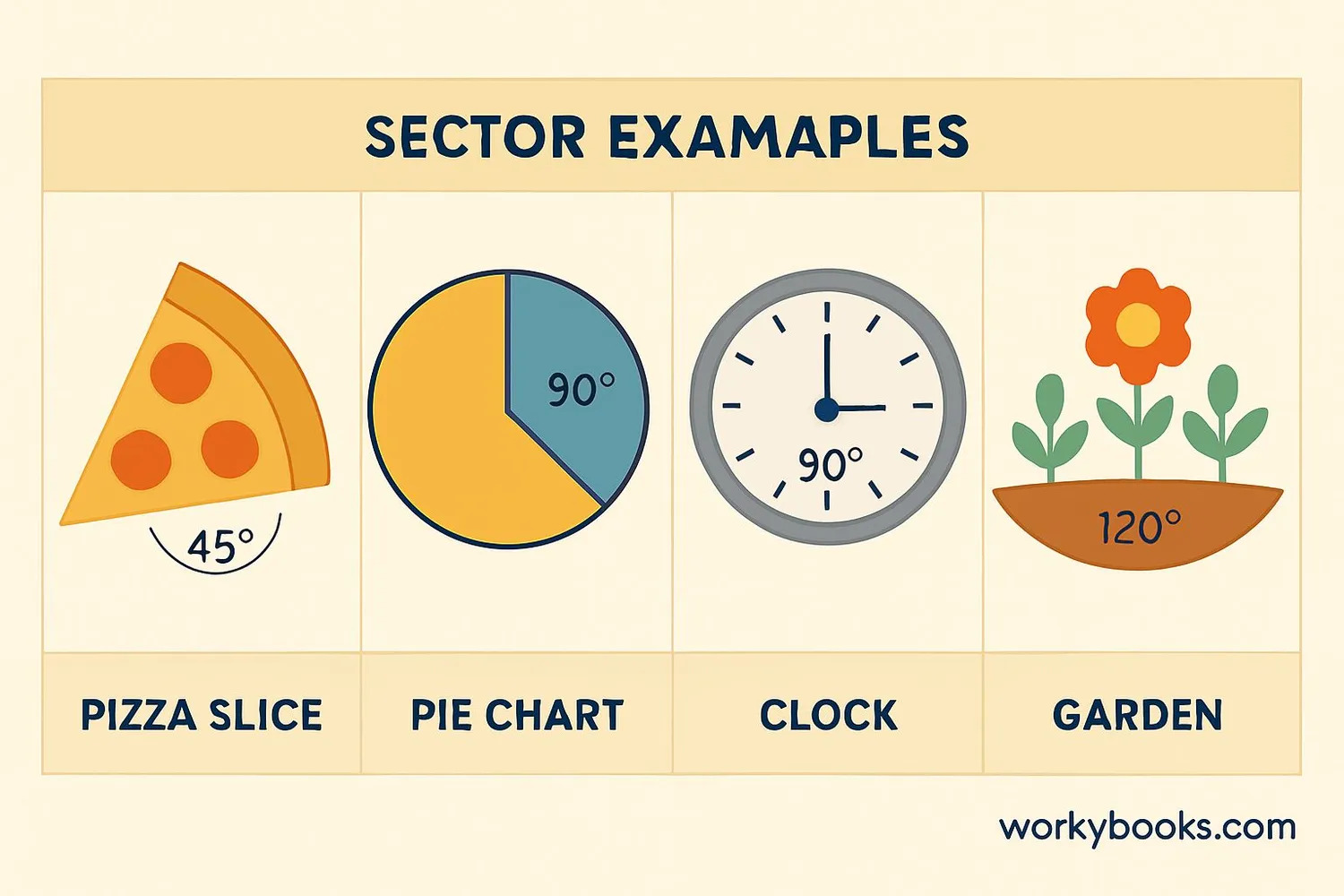
Let's practice with some real-world examples:
Example 1: A pizza has a diameter of 16 inches. If you cut a slice with a 45° angle, what is the area of your slice?
Solution: Radius = diameter/2 = 8 inches
Circle area = π × 8² ≈ 3.14 × 64 = 200.96 in²
Sector fraction = 45/360 = 1/8
Slice area = 200.96 ÷ 8 ≈ 25.12 in²
Example 2: A circular garden with radius 5 meters has a 120° sector planted with flowers. What is the area of the flower section?
Solution: Circle area = π × 5² ≈ 3.14 × 25 = 78.5 m²
Sector fraction = 120/360 = 1/3
Flower area = 78.5 ÷ 3 ≈ 26.17 m²
Example 3: A clock shows the time 3:00. If the minute hand is 10 cm long, what area does it sweep between 12 and 3?
Solution: The angle from 12 to 3 is 90°
Circle area = π × 10² ≈ 3.14 × 100 = 314 cm²
Sector fraction = 90/360 = 1/4
Swept area = 314 ÷ 4 = 78.5 cm²
Calculation Tip
Always simplify the fraction (θ ÷ 360) before multiplying to make calculations easier!
Sector Area Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about sectors:
Circle Trivia
Discover interesting facts about circles and sectors:
Ancient Circles
The ancient Greeks were fascinated by circles. Mathematician Archimedes (287-212 BC) calculated π with remarkable accuracy using polygons with up to 96 sides!
Circular Motion
Planets orbit in elliptical paths, but many man-made satellites use circular orbits. The International Space Station completes a circular orbit every 90 minutes!
Nature's Circles
Nature loves circles! From tree rings to spider webs, circular patterns appear everywhere. Even raindrops make circular ripples when they hit water.
Infinite Sides
Did you know? A circle has infinite sides! As you add more sides to a polygon, it gets closer to being a perfect circle. That's why π has infinite decimal places.





